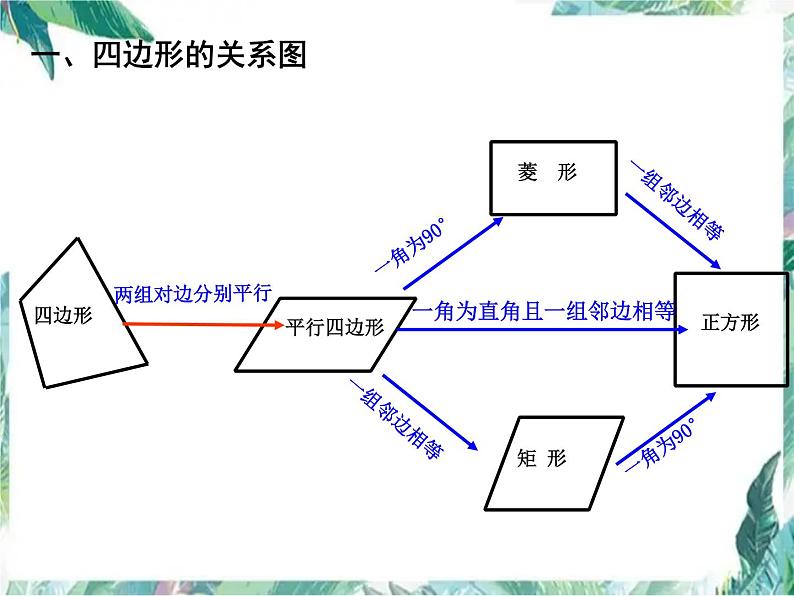
北师大版九年级数学上册-第一章 特殊平行四边形 复习课件

这是一份北师大版九年级数学上册-第一章 特殊平行四边形 复习课件，共22页。PPT课件主要包含了四边形的关系图，分组探究拓展提高，判断题，AC＝BD，我想到，我发现，平行四边形，正方形，a-1，a-2等内容，欢迎下载使用。

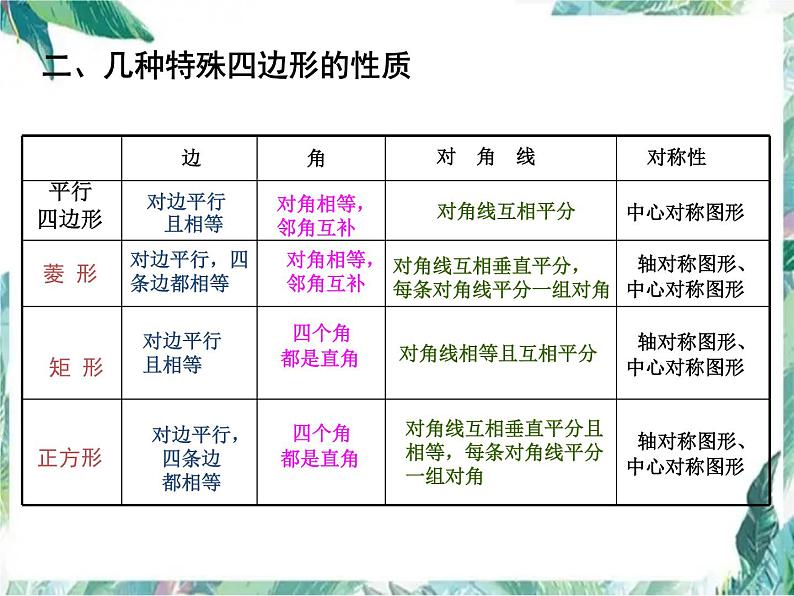
二、几种特殊四边形的性质
对边平行，四条边都相等
对边平行， 四条边 都相等
对角线互相垂直平分，每条对角线平分一组对角
对角线互相垂直平分且相等，每条对角线平分一组对角
轴对称图形、中心对称图形
三、特殊四边形的常用判定方法
（1）两组对边分别平行；
（2）两组对边分别相等；
（4）对角线互相平分；
（5）一组对边平行且相等
（1）有一个角是直角的平行四边形是矩形；
（2）有三个角是直角的四边形是矩形；
（3）对角线相等的平行四边形是矩形。
（1）有一组邻边相等的平行四边形是菱形；
（2）四条边都相等的四边形是菱形；
（3）对角线互相垂直的平行四边形是菱形。
（2）有一组邻边相等的矩形是正方形；
（3）有一个角是直角的菱形是正方形。
（1）有一个角是直角且有一组邻边相等的平行四边形是正方形；
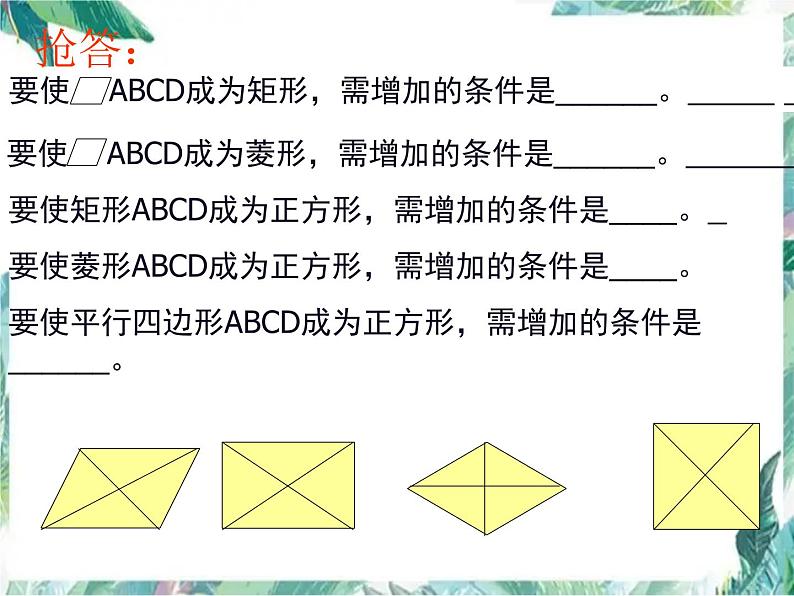
要使矩形ABCD成为正方形，需增加的条件是____。
要使菱形ABCD成为正方形，需增加的条件是____。
要使平行四边形ABCD成为正方形，需增加的条件是______。
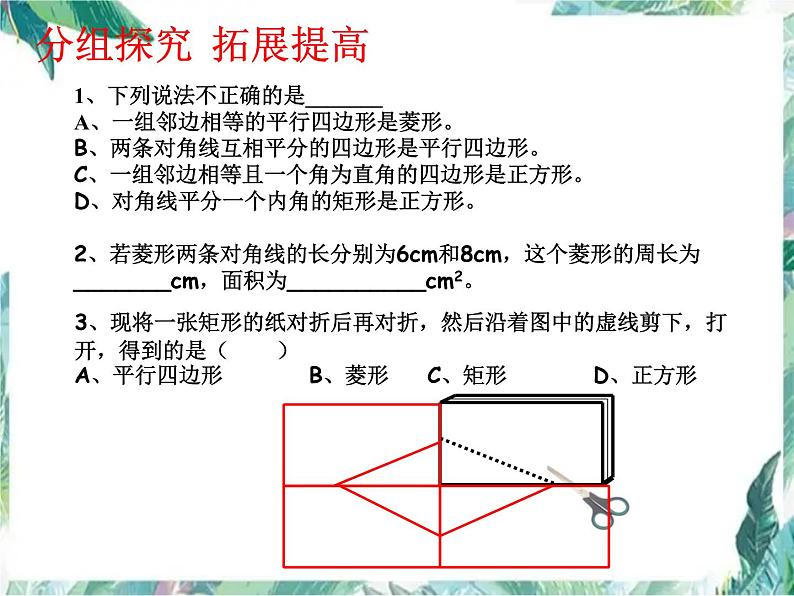
1、下列说法不正确的是_______A、一组邻边相等的平行四边形是菱形。B、两条对角线互相平分的四边形是平行四边形。C、一组邻边相等且一个角为直角的四边形是正方形。D、对角线平分一个内角的矩形是正方形。2、若菱形两条对角线的长分别为6cm和8cm，这个菱形的周长为_______cm，面积为__________cm2。
3、现将一张矩形的纸对折后再对折，然后沿着图中的虚线剪下，打开，得到的是（ ）A、平行四边形 B、菱形 C、矩形 D、正方形
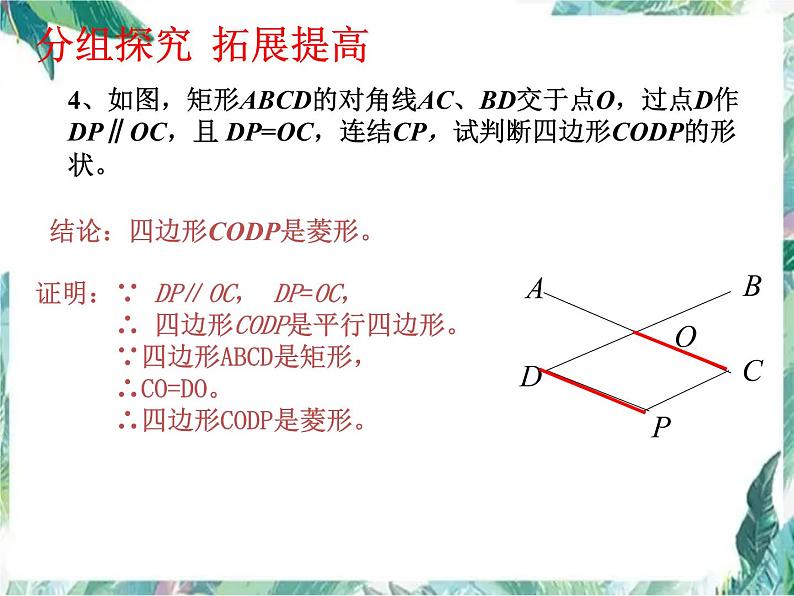
4、如图，矩形ABCD的对角线AC、BD交于点O，过点D作DP∥OC，且 DP=OC，连结CP，试判断四边形CODP的形状。
结论：四边形CODP是菱形。
证明：∵ DP∥OC， DP=OC， ∴ 四边形CODP是平行四边形。 ∵四边形ABCD是矩形，　 ∴CO=DO。 ∴四边形CODP是菱形。
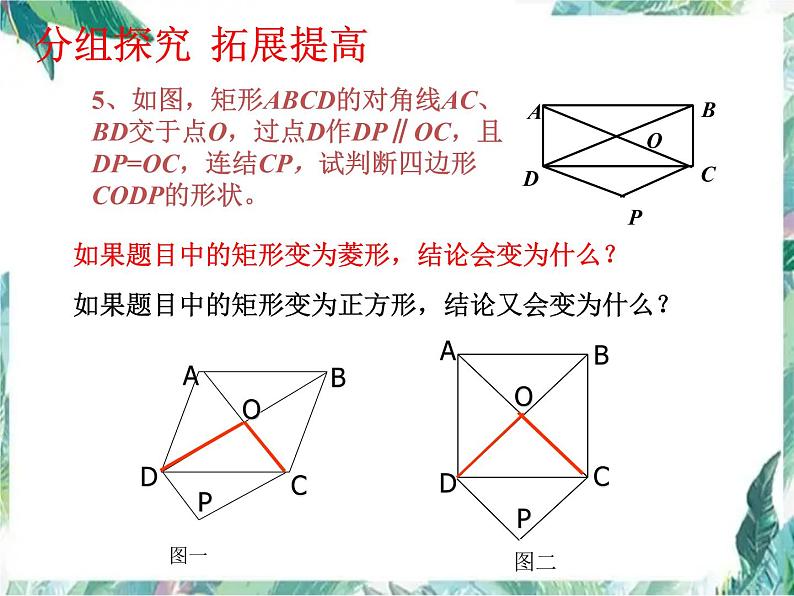
如果题目中的矩形变为正方形，结论又会变为什么？
如果题目中的矩形变为菱形，结论会变为什么？
5、如图，矩形ABCD的对角线AC、BD交于点O，过点D作DP∥OC，且 DP=OC，连结CP，试判断四边形CODP的形状。
（1）一组对边平行，另一组对边相等的的四边形是平行四边形。（ ） （2）两条对角线相等的四边形是矩形。（ ） （3）一组邻边相等的的矩形是正方形。（ ） （4）对角线互相垂直的四边形是菱形。（ ） （5）两条对角线互相平分的四边形是平行四边形。（ ）
7、△ABC中，点O是AC边上的一个动点，过点O作直线M N∥BC，设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F。
（1）求证：EO=FO。（2）当点O运动到何处时，四边形AECF是矩形？并证明你的结论。
（1）证明 ∵ CE 平分∠ ACB ∴ ∠ ACE= ∠ ECB ∵ MN // BC ∴ ∠ ECB= ∠ OEC ∴ ∠ OEC= ∠ ECO ∴ OE=OC同理OF=OC ∴ OE=OF
（2）当O为AC的中点时，四边形AECF是矩形。∵ OA=OC OE=OF∴ 四边形AECN是平行四边形。∵ OE=OC=OF∴ AC=EF∴ 四边形AECN是矩形。
8、菱形纸片ABCD中，两条对角线AC= ，BD= 4 。
（1）求菱形ABCD的面积；
（3） 求∠ADC的度数。
（2）求菱形ABCD的周长；
9、如图，在四边形ABCD中，E、F、G、H分别是边AB、BC、CD、DA的中点，请添加一个条件，使四边形EFGH为菱形，并说明理由。解：添加的条件__________
三角形中位线定理： 三角形的中位线平行于三角形的第三边，且等于第三边的一半。
顺次连接对角线既不相等也不垂直的四边形各边中点得 顺次连接对角线相等但不垂直的四边形各边中点得 顺次连接对角线互相垂直但不相等的四边形各边中点得 顺次连接对角线相等且互相垂直的四边形各边中点得
10、如图，菱形ABCD的对角线的长分别为2和5，P是对角线AC上任一点（点P不与点A、C重合）且PE∥BC交AB于E，PF∥CD交AD于F，则阴影部分的面积是 。
平行四边形被对角线分成的四个三角形面积相等。
11、以△ABC的边AB、AC为边的等边三角形ABD和等边三角形ACE，四边形ADFE是平行四边形。（1）当∠BAC等于 时，四边形ADFE是矩形；（2）当∠BAC等于 时，平行四边形ADFE不存在；（3）当△ABC分别满足什么条件时，平行四边形是菱形、正方形。
解：（3）AB=AC时且∠BAC≠60°，平行四边形ADFE是菱形。AB=AC且∠BAC=150°时，平行四边形ADFE是正方形。
12、如图，矩形纸片ABCD中，AB=3厘米，BC=4厘米，现将A、C重合，使纸片折叠压平，设折痕为EF。试确定重叠部分△AEF的面积。
13、在正方形ABCD中，如图（1）AE⊥BF，AE与BF相等吗？
如图（2）AE⊥HF，AE与HF相等吗？
如图（3）ME⊥HF，ME与HF相等吗？
14、如图所示是一块在电脑屏幕上出现矩形色块图，由6个颜色不同的正方形组成，若中间最小的一个正方形边长为1，你能求出这个矩形色块的面积吗？
由（a-1）+ a= （a-2）+2（a-3）
15、在菱形ABCD中，∠ABC=60°，有一度数为60°的∠MAN绕点A旋转。（1）若∠MAN的两边AM、AN分别交BC、CD于点E、F，则线段CE、DF的大小关系如何？请证明你的结论。（2）若∠MAN的两边AM、AN分别交BC、CD的延长线于点E、F，则线段CE、DF还有（1）中的结论吗？请说明你的理由。
16、运动变化问题的解题方法。
在梯形ABCD中，AD//BC。AD=5，BC=8，M为CD的中点，P是BC边上的一动点（P与B、C不重合）连接PM并延长交AD的延长线于Q。（1）试说明 ≌ 。（2）当P在B、C之间运动。到什么位置时，四边形ABPQ是平行四边形？并说明理由。