

高考数学统考一轮复习第7章立体几何第7节立体几何中的最值翻折探索性问题学案
展开立体几何中的最值、翻折、探索性问题
考点一 立体几何中的最值问题
解决空间图形有关的线段、角、距离、面积、体积等最值问题,一般可以从三方面着手:
一是从问题的几何特征入手,充分利用其几何性质去解决;
二是利用空间几何体的侧面展开图;
三是找出问题中的代数关系,建立目标函数,利用代数方法求目标函数的最值.解题途径很多,在函数建成后,可用一次函数的端点法,二次函数的配方法、公式法,函数有界法(如三角函数等)及高阶函数的拐点导数法等.
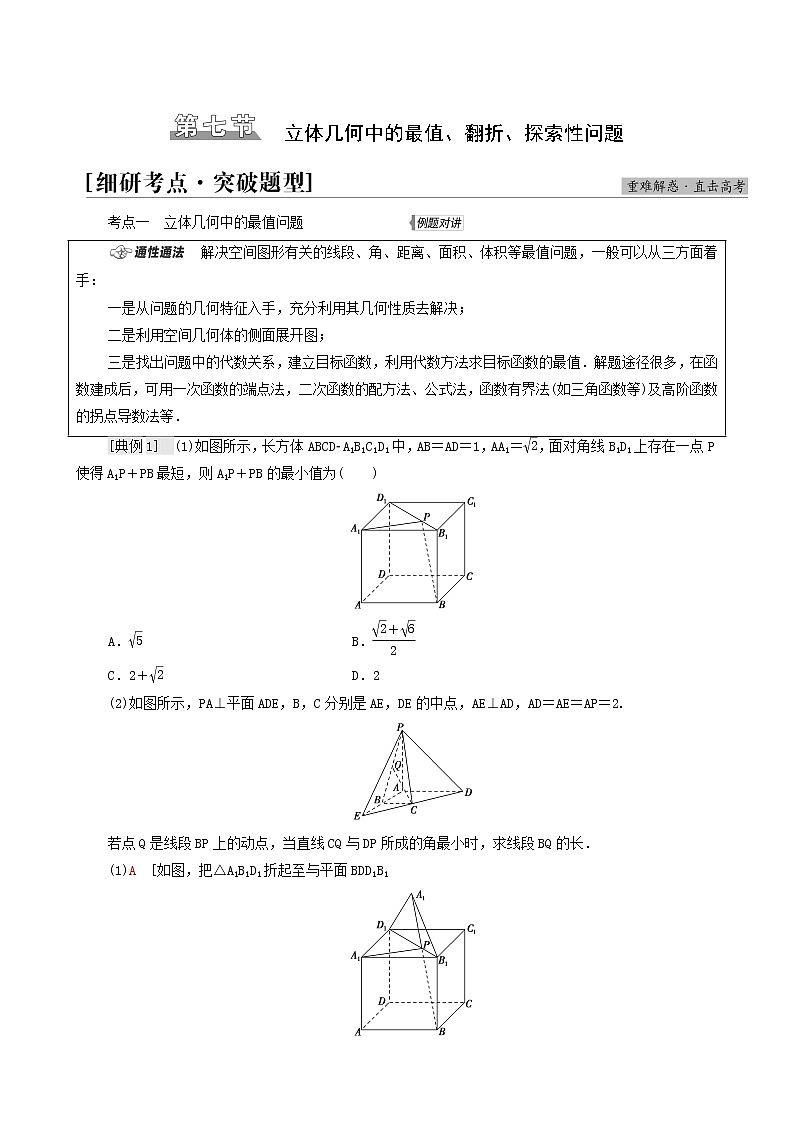
[典例1] (1)如图所示,长方体ABCDA1B1C1D1中,AB=AD=1,AA1=,面对角线B1D1上存在一点P使得A1P+PB最短,则A1P+PB的最小值为( )
A. B.
C.2+ D.2
(2)如图所示,PA⊥平面ADE,B,C分别是AE,DE的中点,AE⊥AD,AD=AE=AP=2.
若点Q是线段BP上的动点,当直线CQ与DP所成的角最小时,求线段BQ的长.
(1)A [如图,把△A1B1D1折起至与平面BDD1B1
共面,连接A1B交B1D1于P,则此时的A1P+PB最短,即为A1B的长,在△A1B1B中,由余弦定理求得A1B=,故选A.]
(2)[解] 因为PA⊥平面ADE,AD⊂平面ADE,AB⊂平面ADE,所以PA⊥AD,PA⊥AB,又因为AE⊥AD,B为AE中点,所以PA,AD,AB两两垂直.
以{,,}为正交基底建立空间直角坐标系Axyz,则各点的坐标为A(0,0,0),B(1,0,0),C(1,1,0),D(0,2,0),P(0,0,2).
=(-1,0,2),故可设=λ=(-λ,0,2λ)(0≤λ≤1).
又=(0,-1,0),所以=+=(-λ,-1,2λ).
又=(0,-2,2),
所以cos〈,〉==.
设1+2λ=t,t∈[1,3],
则cos2〈,〉==≤,
当且仅当t=,
即λ=时,
|cos〈,〉|的最大值为.
因为y=cos x在上是减函数,
所以当λ=时直线CQ与DP所成角取得最小值.
又因为BP==,所以BQ=BP=.
点评:本例(1)属于线段和的最值问题,求解时采用了化空间为平面,化折为直的重要手段;本例(2)属于解决空间角的最值问题,求解时采用了把空间角的余弦三角函数值表示为参数λ的二次函数,利用这个函数的单调性求三角函数值的最值,求解时需要注意的是函数中自变量的取值范围对最值的决定作用.
(2020·广州模拟)如图所示,在四面体ABCD中,AD⊥AB,平面ABD⊥平面ABC,AB=BC=AC,且AD+BC=4.
(1)证明:BC⊥平面ABD;
(2)设E为棱AC的中点,当四面体ABCD的体积取得最大值时,求二面角CBDE的余弦值.
[解] (1)证明:因为AD⊥AB,平面ABD⊥平面ABC,平面ABD∩平面ABC=AB,AD⊂平面ABD,
所以AD⊥平面ABC,
因为BC⊂平面ABC,所以AD⊥BC.
因为AB=BC=AC,
所以AB2+BC2=AC2,
所以AB⊥BC,
因为AD∩AB=A,所以BC⊥平面ABD.
(2)设AD=x(0<x<4),则AB=BC=4-x,
四面体ABCD的体积
V=f (x)=x×(4-x)2
=(x3-8x2+16x)(0<x<4).
f ′(x)=(3x2-16x+16)=(x-4)(3x-4),
当0<x<时,f ′(x)>0,V=f (x)单调递增;
当<x<4时,f ′(x)<0,V=f (x)单调递减.
故当AD=x=时,四面体ABCD的体积取得最大值.
以B为坐标原点,建立空间直角坐标系Bxyz,
则B(0,0,0),A,C,D,E.
设平面BCD的法向量为n=(x,y,z),
则,即
令z=-2,得n=(0,1,-2),
同理可得平面BDE的一个法向量为m=(1,-1,2),
则cos〈m,n〉===-.
由图可知,二面角CBDE为锐角,故二面角CBDE的余弦值为.
考点二 平面图形的翻折问题
三步解决平面图形翻折问题
[典例2] (2018·全国卷Ⅰ)如图,四边形ABCD为正方形,E,F分别为AD,BC的中点,以DF为折痕把△DFC折起,使点C到达点P的位置,且PF⊥BF.
(1)证明:平面PEF⊥平面ABFD;
(2)求DP与平面ABFD所成角的正弦值.
[解] (1)证明:由已知可得BF⊥PF,BF⊥EF,
PF∩EF=F,PF,EF⊂平面PEF,
所以BF⊥平面PEF.
又BF⊂平面ABFD,
所以平面PEF⊥平面ABFD.
(2)如图,作PH⊥EF,垂足为H.
由(1)得,PH⊥平面ABFD.
以H为坐标原点,的方向为y轴正方向,||为单位长,建立如图所示的空间直角坐标系Hxyz.
由(1)可得,DE⊥PE.
又DP=2,DE=1,所以PE=.
又PF=1,EF=2,
所以PE⊥PF.
所以PH=,EH=.
则H(0,0,0),P,D,
=,=.
又为平面ABFD的法向量,
设DP与平面ABFD所成的角为θ,
则sin θ=|cos〈,〉|===.
所以DP与平面ABFD所成角的正弦值为.
点评:平面图形翻折为空间图形问题重点考查平行、垂直关系,解题关键是看翻折前后线面位置关系的变化,根据翻折的过程找到翻折前后线线位置关系中没有变化的量和发生变化的量,这些不变的和变化的量反映了翻折后的空间图形的结构特征.
如图①,在高为6的等腰梯形ABCD中,AB∥CD,且CD=6,AB=12,将它沿对称轴OO1折起,使平面ADO1O⊥平面BCO1O,如图②,点P为BC的中点,点E在线段AB上(不同于A,B两点),连接OE并延长至点Q,使AQ∥OB.
图① 图②
(1)证明:OD⊥平面PAQ;
(2)若BE=2AE,求二面角CBQA的余弦值.
[解] (1)证明:由题设知OA,OB,OO1两两垂直,
∴以O为坐标原点,OA,OB,OO1所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,
设AQ的长为m,则O(0,0,0),A(6,0,0),B(0,6,0),C(0,3,6),D(3,0,6),Q(6,m,0).
∵点P为BC的中点,
∴P,
∴=(3,0,6),=(0,m,0),=.
∵·=0,·=0,
∴⊥,⊥,
即OD⊥AQ,OD⊥PQ,又AQ∩PQ=Q,
∴OD⊥平面PAQ.
(2)∵BE=2AE,AQ∥OB,∴AQ=OB=3,
则Q(6,3,0),∴=(-6,3,0),=(0,-3,6).
设平面CBQ的法向量为n1=(x,y,z),
由
得
令z=1,则y=2,x=1,n1=(1,2,1).
易得平面ABQ的一个法向量为n2=(0,0,1).
设二面角CBQA的大小为θ,由图可知,θ为锐角,
则cos θ==,
即二面角CBQA的余弦值为.
考点三 立体几何中的探索性问题
(1)解决探索性问题的基本方法是假设结论成立或对象存在,然后在这个前提下进行逻辑推理,若能推导出与条件吻合的数据或事实,则说明假设成立,即存在,并可进一步证明;否则不成立,即不存在.
(2)在棱上探寻一点满足各种条件时,要明确思路,设点坐标,应用共线向量定理a=λb(b≠0),利用向量相等,所求点坐标用λ表示,再根据条件代入,注意λ的范围.
(3)利用空间向量的坐标运算,可将空间中的探索性问题转化为方程是否有解的问题进行处理.
[典例3](2020·上饶模拟)如图所示,正方形AA1D1D与矩形ABCD所在平面互相垂直,AB=2AD=2,点E为AB的中点.
(1)求证:BD1∥平面A1DE;
(2)设在线段AB上存在点M,使二面角D1MCD的大小为,求此时AM的长及点E到平面D1MC的距离.
[解] (1)证明:连接AD1,交A1D于点O,∵四边形AA1D1D为正方形,
∴O是AD1的中点,∵点E为AB的中点,连接OE.
∴EO为△ABD1的中位线,∴EO∥BD1.
又∵BD1⊄平面A1DE,OE⊂平面A1DE,∴BD1∥平面A1DE.
(2)由题意可得D1D⊥平面ABCD,以点D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,则D(0,0,0),C(0,2,0),A1(1,0,1),D1(0,0,1),B(1,2,0),E(1,1,0),
设M(1,y0,0)(0≤y0≤2),
∵=(-1,2-y0,0),=(0,2,-1),
设平面D1MC的一个法向量为n1=(x,y,z),
则即
令y=1,有n1=(2-y0,1,2).
而平面MCD的一个法向量为n2=(0,0,1).
要使二面角D1MCD的大小为,
则cos =|cos〈n1,n2〉|===,
解得y0=2-(0≤y0≤2),故AM=2-,此时
n1=,=(1,1,-1).
故点E到平面D1MC的距离为d===.
点评:求空间距离常用的方法
(1)直接法:利用线线垂直、线面垂直、面面垂直等性质定理与判定定理,作出垂线段,再通过解三角形求出距离.
(2)间接法:利用等体积法、特殊值法等转化求解.
(3)向量法:空间中的距离问题一般都可转化为点到平面的距离问题进行求解.
求点P到平面α的距离的步骤:
①在平面α内取一点A,确定向量的坐标;
②确定平面α的法向量n;
③代入公式d=求解.
(2020·沈阳模拟)如图,已知直三棱柱ABCA1B1C1中,AA1=AB=AC=1,AB⊥AC,M,N,Q分别是CC1,BC,AC的中点,点P在直线A1B1上运动,且=λ(λ∈[0,1]).
(1)证明:无论λ取何值,总有AM⊥平面PNQ;
(2)是否存在点P,使得平面PMN与平面ABC的夹角为60°?若存在,试确定点P的位置,若不存在,请说明理由.
[解] (1)如图,以A为坐标原点,AB,AC,AA1所在的直线分别为x轴、y轴、z轴建立空间直角坐标系,
则A(0,0,0),A1(0,0,1),B1(1,0,1),M,N,Q,
由=λ=λ(1,0,0)=(λ,0,0),可得点P(λ,0,1),所以=,=.
又=,所以·=0+-=0,·=0+-=0,
所以⊥,⊥,即AM⊥PN,AM⊥PQ,
又PN∩PQ=P,所以AM⊥平面PNQ,
所以无论λ取何值,总有AM⊥平面PNQ.
(2)设n=(x,y,z)是平面PMN的法向量,
=,=,
则即得
令x=3,所以n=(3,1+2λ,2-2λ)是平面PMN的一个法向量.
取平面ABC的一个法向量为m=(0,0,1).
假设存在符合条件的点P,则
|cos〈m,n〉|==,
化简得4λ2-14λ+1=0,解得λ=或λ=(舍去).
综上,存在点P,且当A1P=时,满足平面PMN与平面ABC的夹角为60°.
高考数学一轮复习第7章第8课时向量法求距离及立体几何中的探索性、翻折问题学案: 这是一份高考数学一轮复习第7章第8课时向量法求距离及立体几何中的探索性、翻折问题学案,共27页。
2024年高考数学第一轮复习精品导学案第57讲 立体几何中翻折问题(学生版)+教师版: 这是一份2024年高考数学第一轮复习精品导学案第57讲 立体几何中翻折问题(学生版)+教师版,共2页。学案主要包含了题型选讲,折叠问题,折叠的综合性问题等内容,欢迎下载使用。
第52讲 立体几何中的动点与翻折问题: 这是一份人教A版 (2019)必修 第一册全册综合学案设计,共2页。












