2021-2022学年四川省眉山市高二（下）期末数学试卷（理科）（Word解析版）

这是一份2021-2022学年四川省眉山市高二（下）期末数学试卷（理科）（Word解析版），共19页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
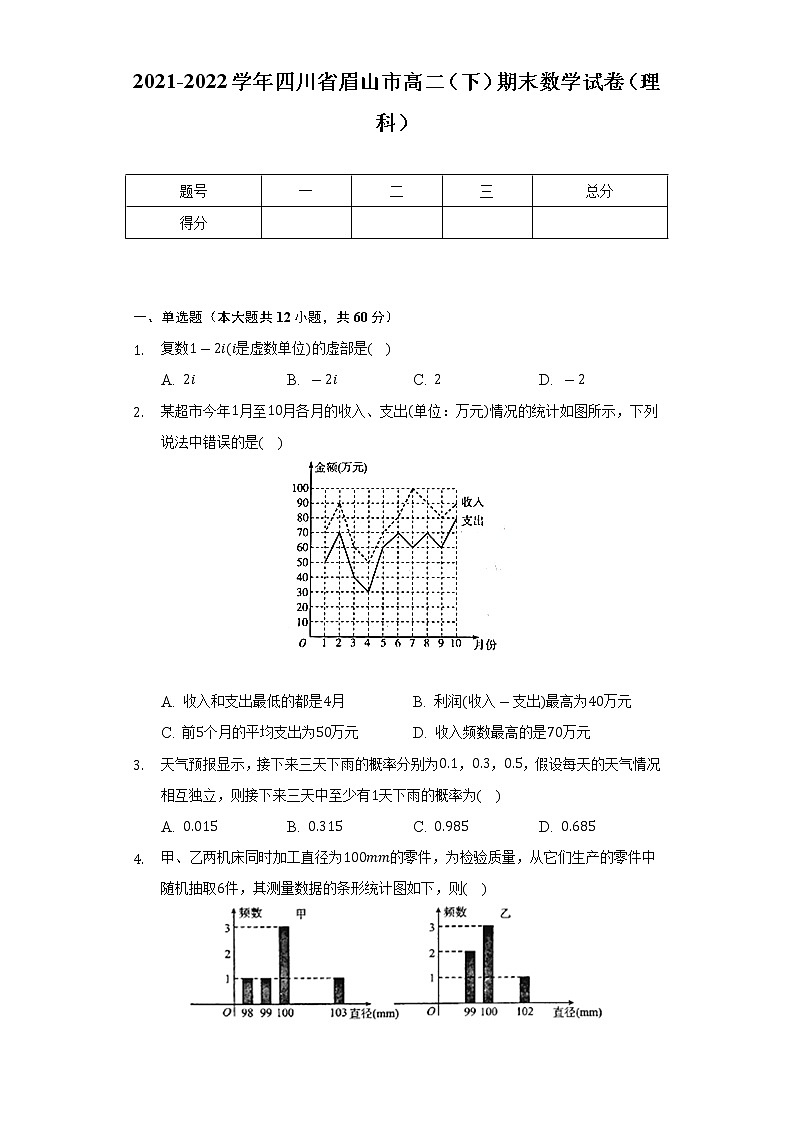
2021-2022学年四川省眉山市高二（下）期末数学试卷（理科） 题号一二三总分得分      一、单选题（本大题共12小题，共60分）复数是虚数单位的虚部是(    )A.  B.  C.  D. 某超市今年月至月各月的收入、支出单位：万元情况的统计如图所示，下列说法中错误的是(    )
A. 收入和支出最低的都是月 B. 利润收入支出最高为万元
C. 前个月的平均支出为万元 D. 收入频数最高的是万元天气预报显示，接下来三天下雨的概率分别为，，，假设每天的天气情况相互独立，则接下来三天中至少有天下雨的概率为(    )A.  B.  C.  D. 甲、乙两机床同时加工直径为的零件，为检验质量，从它们生产的零件中随机抽取件，其测量数据的条形统计图如下，则(    )
A. 甲的数据的平均数大于乙的数据的平均数
B. 甲的数据的中位数大于乙的数据的中位数
C. 甲的数据的方差大于乙的数据的方差
D. 甲的数据的极差小于乙的数据的极差某班最近一次化学考试成绩的频率分布直方图如图所示，若化学老师欲将大家的成绩由高到低排列，并奖励排名在前的同学，试估计化学老师选取的学生分数应不低于(    )
A.  B.  C.  D. “结绳计数”是远古时期人类智慧的结晶，即人们通过在绳子上打结来记录数量．如图所示的是一位农民记录自己采摘果实的个数．在从右向左依次排列的不同绳子上打结，满四进一．根据图示可知，农民采摘的果实的个数是(    )
A.  B.  C.  D. 某中学举行的秋季运动会中，有甲、乙、丙、丁四位同学参加米短跑决赛，现将四位同学安排在，，，这个跑道上，每个跑道安排一名同学，则甲不在跑道，乙不在跑道的不同安排方法种数为(    )A.  B.  C.  D. 某同学为了模拟测定圆周率，设计如下方案：向圆内随机扔入颗芝麻，其不等式表示区域内的粒数为，则下面各式的值可近似等于圆周率的是(    )A.  B.  C.  D. 用数学归纳法证明时，由到，左边需要添加的项数为(    )A.  B.  C.  D. 秦九韶是我国南宋时期的数学家，他在所著数书九章中提出的多项式求值算法，至今仍是比较先进的算法如图是秦九韶算法的一个程序框图，执行该程序框图，若输入，，输出，则输入的实数的值为(    )A. 或
B. 或
C. 或
D. 或
 已知定义在上的可导函数满足，设，，则，的大小关系是(    )A.  B.  C.  D. 不确定已知实数，，满足，，若，则(    )A.  B.  C.  D.  二、填空题（本大题共4小题，共20分）是虚数单位，复数满足，则______．某学校为了了解学生的学习情况，用系统抽样的方法从全校名学生中抽取人进行调查．现将名学生随机地从编号，按编号顺序平均分成组，若第组抽出的号码为，则第组抽到的号码是______．为积极应对人口老龄化，年月日，全国人大常委会会议表决通过了关于修改人口与计划生育法的决定，提倡适龄婚育、优生优育，一对夫妻可以生育三个子女．若已知某个家庭有个小孩，且其中至少有个男孩的条件下，则第三个孩子是女孩的概率为______．已知函数在处的切线方程为，给出以下结论：
在定义域上不单调
，
有唯一零点若，则
其中所有正确结论的序号是______． 三、解答题（本大题共6小题，共70分）某校高二班的一次化学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损，可见部分如图：

求全班人数及全班分数的中位数；
根据频率分布直方图估计该班本次测试的平均成绩同一组中的数据用该组区间的中点值为代表；
若从分数在及的答题卡中采用分层抽样的方式抽取了份答题卡，再从抽取的这份答题卡中随机抽取份答题卡了解学生失分情况，求这份答题卡至少有一份分数在的概率．已知二项式的展开式中前三项的二项式系数和等于．
求展开式中项的系数；
记，求的值．司机在开机动车时使用手机是违法行为，会存在严重的安全隐患，危及自己和他人的生命．为了研究司机开车时使用手机的情况，交警部门调查了名机动车司机，得到以下统计：在名男性司机中，开车时使用手机的有人，开车时不使用手机的有人；在名女性司机中，开车时使用手机的有人，开车时不使用手机的有人．
Ⅰ完成下面的列联表，并判断是否有的把握认为开车时使用手机与司机的性别有关； 开车时使用手机开车时不使用手机合计男性司机人数   女性司机人数   合计   Ⅱ以上述的样本数据来估计总体，现交警部门从道路上行驶的大量机动车中随机抽检辆，记这辆车中司机为男性且开车时使用手机的车辆数为，若每次抽检的结果都相互独立，求的分布列和数学期望．
参考公式与数据：，其中．某收费手机应用程序自上架以来，凭借简洁的界面设计、方便的操作方式和实用的强大功能深得用户喜爱．为回馈市场并扩大用户量，该在年以竞价形式做出优惠活动，活动规则如下：每月到日，大家可通过官网提交自己的报价报价低于原价，但在报价时间截止之前无法得知其他人的报价和当月参与活动的总人数；当月竞价时间截止后的第二天，系统将根据当期优惠名额，按出价从高到低的顺序给相应人员分配优惠名额，获得优惠名额的人的最低出价即为该在当月的下载优惠价，出价不低于优惠价的人将获得数额为原价减去优惠价的优惠券，并可在当月下载该时使用．小明拟参加年月份的优惠活动，为了预测最低成交价，他根据网站的公告统计了今年到月参与活动的人数，如下表所示：时间月参与活动的人数万人若可用线性回归模型拟合参与活动的人数单位：万人与时间单位：月之间的关系，请用最小二乘法求关于的回归方程，并预测今年月参与活动的人数；
某自媒体对位拟参加今年月份活动的人进行了一个抽样调查，得到如表所示的频数表：报价单位：元频数求这人的报价单位：元的平均值和方差同一区间的报价用该价格区间的中点值代替；
假设所有参与活动的人的报价单位：元可视为服从正态分布，且与可分别由中所求的样本平均数及估计，若年月计划发放优惠名额数量为，请你合理预测该在当月的下载优惠价，并说明理由．
参考公式及数据：回归方程，，；
，，；
若随机变量服从正态分布，则，，．已知函数，，
讨论函数的单调性；
证明：函数在定义域上只有一个零点．已知
求的极值点；
若不等式存在正数解，求实数的取值范围．
答案和解析 1.【答案】 【解析】解：是虚数单位的虚部是．
故选：．
利用复数虚部的定义即可得出．
本题考查了复数的虚部的定义，属于基础题．
 2.【答案】 【解析】解：选项A，收入和支出都在月达到峰底，即A正确；
选项B，利润最高时，对应的月份是月，收入为万元，支出为万元，所以利润为万元，即B正确；
选项C，前个月的支出分别为，，，，，所以平均支出为万元，即C正确；
选项D，这个月的收入分别为，，，，，，，，，，所以频数最高的是万元，即D错误．
故选：．
根据折线图中的数据与变化趋势，逐一分析即可．
本题考查对折线图的认识，考查学生对数据的分析与处理能力，属于基础题．
 3.【答案】 【解析】解：接下来三天中至少有天下雨的概率为，
故选：．
利用间接法，结合独立事件的概率乘法公式求解．
本题主要考查了独立事件的概率乘法公式，属于基础题．
 4.【答案】 【解析】解：甲的数据的平均数为，
乙的数据的平均数为，
故选项A错误；
甲的数据的中位数为，乙的数据的中位数为，
故选项B错误；
甲的数据的方差为，
乙的数据的方差为，
故甲的数据的方差大于乙的数据的方差，
即选项C正确；
甲的数据的极差为，
乙的数据的极差为，
故选项D错误；
故选：．
对于选项A，根据条形统计图分别求甲、乙数据的平均数即可判断；
对于选项B，根据条形统计图分别求甲、乙数据的中位数即可判断；
对于选项C，根据条形统计图分别求甲、乙数据的方差即可判断；
对于选项D，根据条形统计图分别求甲、乙数据的极差即可判断．
本题考查了平均数、中位数、方差与极差的求法，属于基础题．
 5.【答案】 【解析】解：由题意得，
，
解得，
而，
，
故估计化学老师选取的学生分数应不低于分，
故选：．
由频率分布直方图面积之和为列方程求，再求对应的分数即可．
本题考查了频率分布直方图的应用，属于基础题．
 6.【答案】 【解析】【分析】
本题考查进位制及进行简单的合情推理，属于简单题．
结合进位制进行简单的合情推理得：农民采摘的果实的个数是，计算得解．
【解答】
解：由题意有：农民采摘的果实的个数是．
故选C．  7.【答案】 【解析】解：根据题意，分种情况讨论：
若甲在道上，剩下人任意安排在其他个跑道上，有种排法．
若甲不在道上，甲的安排方法有种，乙的安排方法也有种，剩下人任意安排在其他个跑道上，有种安排方法．
此时有种安排方法．
故共有种不同的安排方法．
故选：．
根据题意，按甲是否在上分种情况讨论，求出每种情况的安排方法数目，由加法原理计算可得答案．
本题主要考查简单的排列组合，属于基础题．
 8.【答案】 【解析】解：根据题意画出图形；
如图所示：

故，，
所以，整理得．
故选：．
直接利用不等式所表示的平面区域和几何概型问题的应用求出结果．
本题考查的知识要点：不等式表示的平面区域，几何概型问题的应用，主要考查学生的运算能力和数学思维能力，属于中档题．
 9.【答案】 【解析】解：当时，等式左端为，
当时，等式左端为，
所以共增加了项．
故选：．
写出时和时等式左边式子，比较即可．
本题考查了数学归纳法，属于基础题．
 10.【答案】 【解析】解：由题意，模拟程序的运行，
可得，；，；
执行循环体，，；
不满足退出循环的条件，执行循环体，，；
不满足退出循环的条件，执行循环体，，；
此时，满足退出循环的条件，退出循环，输出的值为，
整理可得，解得或．
故选：．
由已知中的程序语句可知：该程序的功能是利用循环结构计算并输出变量的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．
本题考查了程序框图的应用问题，解题时应模拟程序框图的运行过程，是基础题．
 11.【答案】 【解析】解：记，因为，所以，
则在上单调递减，
因为所以所以，
即，
整理得，即．
故选：．
构造函数，求导，结合已知可得单调性，然后利用单调性可得．
本题考查利用导数研究函数的单调性，考查学生的运算能力，属于中档题．
 12.【答案】 【解析】解：由，得；由，得，
两式相加得，因为，，
所以，又因为，所以；
因为，所以，即，所以．
令，则，
当时，，
所以在内单调递增，即，
所以，即，
又令，则，
当时，，所以在内单调递增，
所以由，得到．
所以．
故选：．
首先根据题中的条件得到，从而得到；再根据时，得到，结合函数的单调性得到，从而得到．
本题考查利用导数研究函数的单调性，考查学生的运算能力，属于中档题．
 13.【答案】 【解析】解：，
，
．
故答案为：．
根据已知条件，运用复数的运算法则，以及复数模的公式，即可求解．
本题主要考查复数的运算法则，以及复数的模，属于基础题．
 14.【答案】 【解析】解：由题设，抽取间隔为．
所以第组抽到的号码是．
故答案为：．
根据系统抽样中等距抽样的方法，计算出抽样间隔，结合第组抽取号码确定第组的号码．
本题主要考查系统抽样，属于基础题．
 15.【答案】 【解析】解：个小孩可能发生的事件如下：
男男男，男男女，男女女，男女男，女女女，女女男，女男女，女男男，共种，
设至少有一个男孩，第三个孩子是女孩，
则，，
某个家庭有个小孩，且其中至少有个男孩的条件下，第三个孩子是女孩的概率为：
．
故答案为：．
根据条件概率公式能求出第三个孩子是女孩的概率．
本题考查概率的求法，考查条件概率等基础知识，考查运算求解能力，是基础题．
 16.【答案】 【解析】解：因为，则，
因为函数在处的切线方程为，所以，，即，解得，，
所以，
对于，，又，所以在上恒成立，所以函数在上单调递减，故不正确；
对于，因为函数在上单调递减，且，所以当，要使成立，则，
所以，整理得，解得与矛盾，故不正确；
对于，因为函数在上单调递减，且，所以函数有唯一零点，故正确；
对于因为，
所以由得，所以，即，故正确；
故答案为：．
求导函数，由导函数的几何意义得，，由此求得，，得函数的解析式，对于，求导得在上恒成立，由此可判断；
对于，由函数在上单调递减，且，得当，要使成立，则，解得，由此判断；对于，由函数在上单调递减，且，可判断：对于，由，得，由此可判断．
本题考查利用导数求函数的最值，考查学生的运算能力，属于中档题．
 17.【答案】解：由茎叶图得分数在内的频数为，
由频率分布直方图得分数在的频率为，
全班人数为，
分数在内的频数为，分数在内的频数为，
全班分数的中位数为．
由茎叶图得分数在内的频数为，
在内的频数为，分数在内的频数为，
在内的频数为，
分数在内的频数为，
该班本次测试的平均成绩为：
．
分数在内的频数为，在内的频数为，
由分层抽样抽取了份答题卡中，
分数在内的有份，分别记为，，，分数在内有份，分别记为，，
从抽取的份答题卡中随机抽取份基本事件有种，分别为：
，，，，，，，，，，
其中这份答题卡至少有一份分数在包含的基本事件有种，分别为：
，，，，，，，
这份答题卡至少有一份分数在的概率为． 【解析】根据茎叶图与频率分布直方图中分数在内数据求得全班人数为人，进而能求出中位数；
根据频率分布直方图平均数的计算方法能求出该班本次测试的平均成绩；
根据题意抽取了份答题卡中，分数在内有份，分数在内有份，再结合古典概型能求出这份答题卡至少有一份分数在的概率．
本题考查样本单元数、中位数、平均数、概率等基础知识，考查运算求解能力，是基础题．
 18.【答案】解：前三项的二项式系数和等于，所以，解得．
故二项展开式的通项为：，令，解得．
故系数为．
令，解得．
令，得到．
因为时最高次，所以，解得．
则 【解析】先根据前三项的二项式系数和等于求出的值，再利用二项展开式的通项求解即可．
分别令，解得，再令得到，再求出，求解即可．
本题主要考查二项式定理，属于中档题．
 19.【答案】解：Ⅰ填写列联表，如下； 开车时使用手机开车时不使用手机合计男性司机人数女性司机人数合计根据数表，计算，
所以有的把握认为开车时使用手机与司机的性别有关；
Ⅱ由题意，任意抽取辆车中司机为男性且开车时使用手机的概率是，
则的可能取值为：，，，，且，
可得，
所以，
，
，
；
所以的分布列为：数学期望为． 【解析】Ⅰ根据题意填写列联表，计算观测值，对照临界值得出结论；
Ⅱ求出任意抽取辆车中司机为男性且开车时使用手机的概率，
知的可能取值，且服从二项分布，计算对应的概率，
写出的分布列，计算数学期望值．
本题考查了二项分布列的性质及其数学期望和独立性检验思想方法，属于中档题．
 20.【答案】解：由题意可得，
，
又因为，
所以，
，
所以回归直线方程为：，
当时，可得万人，
故预计今年月参与活动的人数为万人；
解：依题意可得这人的报价单位：元的平均值，
，
方差，
由可知，依题意发放的优惠名额为张，预测参加的人数为人，
所以能够得到优惠名额的概率，
设下载优専价为，则，
又，因为，
所以，
则，
所以预测该在当月的下载优惠价为元． 【解析】根据所给数据求出，即可求出，即可求出回归直线方程，再令代入计算可得；
根据平均数、方差公式计算可得；
依题意可得，再由能得到优惠名额的概率，再根据正态分布的性质计算可得．
本题考查线性回归方程，考查学生的运算能力，属于难题．
 21.【答案】解：，，，
令得，或，
当时，，
在上，，单调递减，
当时，令，得，
令，得，，
当时，令，得，
令，得，，
综上所述，当时，在上单调递减，
当时，在上单调递增，在，上单调递减，
当时，在上单调递增，在，上单调递减．
证明：由函数的单调性可知，
当时，，在上单调递减，
，
，，
所以，
所以函数在上只有一个零点，
当时，在上单调递增，在，上单调递减，

所以函数在上无零点，
，
，
所以，
所以在上有一个零点，
所以函数在上只有一个零点．
当时，在上单调递增，在，上单调递减，
，，
所以，
所以函数在上有一个零点，
，
，
所以在上没有零点，
所以函数在上只有一个零点． 【解析】求导得，令得或，分三种情况：当时，当时，当时，讨论的单调性．
由可知函数的单调性，求出极值，结合函数的零点存在性定理，即可得出答案．
本题考查导数的综合应用，解题中注意分类讨论思想的应用，属于中档题．
 22.【答案】解：的定义域为，，
令，可得或，列表如下：          增 极大值减 极小值增所以，的极大值点为，极小值点为；
由题意可知，存在，使得，即，
令，其中，则，
令，其中，则，
令，其中，则，
所以在上单调递增，则，
所以函数在上单调递增，则，
所以当时，，函数单调递减，
当时，，函数单调递增，则，
所以．
实数的取值范围为． 【解析】，令，可求极值点；
由已知可得，令，求导，可令，再求导，进而可判断当时，，函数单调递减，当时，，函数单调递增，可求
本题考查求函数的极值，考查利用求函数的最值求参数的取值范围，属难题．