人教A版 (2019)选择性必修 第一册3.2 双曲线精品ppt课件

课题

双曲线的简单几何性质（一）

教学目标

1.掌握并会应用双曲线的简单几何性质；理解双曲线的渐近线及离心率的意义；

2.通过学习提升直观想象素养、培养逻辑推理及数学运算的能力.

教学重点

双曲线的简单几何性质及其应用。

教学难点

灵活应用已知条件解决与双曲线的几何性质及标准方程、定义有关的问题。

教学准备

教师准备：PPT课件。

学生准备：预习课本P121—P124

教学过程

一、导入新课：

欣赏现实生活中的双曲线：

观察图形，猜想双曲线有哪些几何性质？

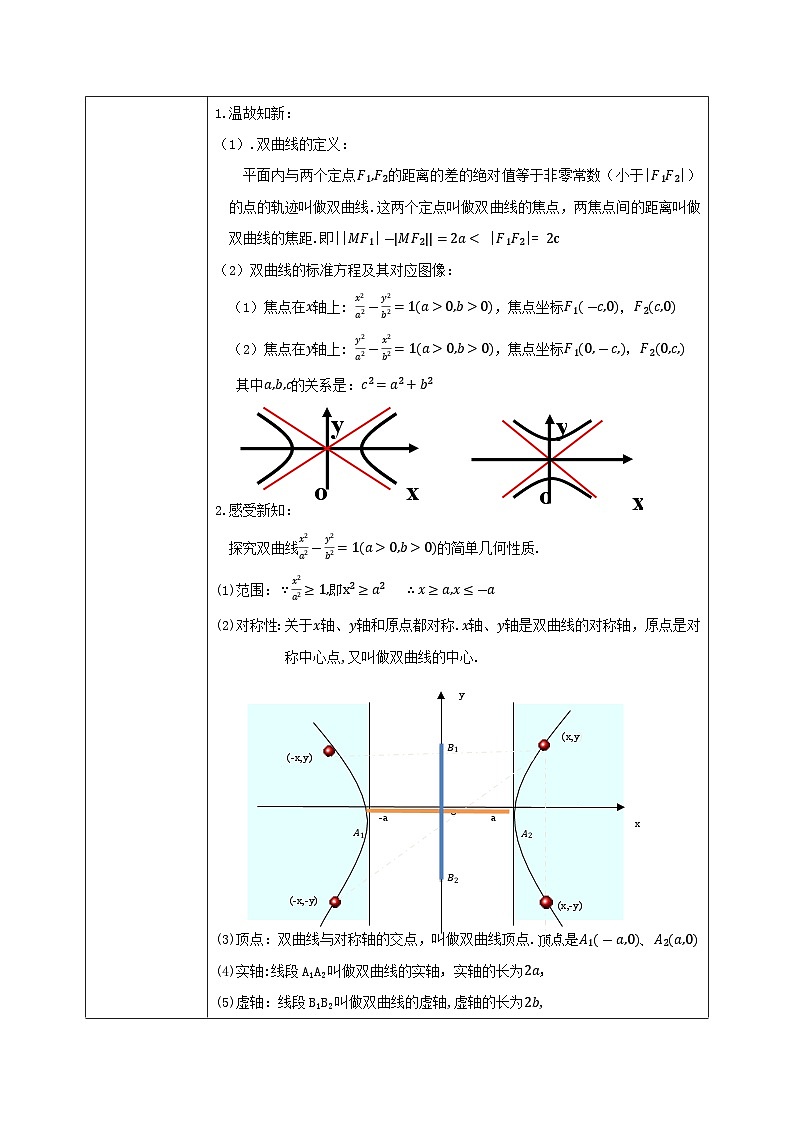
老师通过PPT向学生展示现实生活中与双曲线有关的实际图形，提出问题，引起悬念，从而导出新课，进一步启发学生用已有知识猜想和推导双曲线的几何性质，渗透和提升转化与化归思想的应用，进而学习这节课的内容。

二、知识梳理：

       通过上面的问题，提出问题，引起悬念，进一步带领学生探究双曲线的几何性质以及解决此类数学问题的方法。阅读课本P121-P124，回答下列问题：

1.温故知新：

（1）.双曲线的定义：

    平面内与两个定点的距离的差的绝对值等于非零常数（小于||）的点的轨迹叫做双曲线.这两个定点叫做双曲线的焦点，两焦点间的距离叫做双曲线的焦距.即||| ||=

（2）双曲线的标准方程及其对应图像：

  （1）焦点在轴上: ，焦点坐标

（2）焦点在轴上: ，焦点坐标

   其中的关系是：

2.感受新知：

探究双曲线的简单几何性质.

(1)范围：

(2)对称性：关于轴、轴和原点都对称.轴、轴是双曲线的对称轴，原点是对称中心点,又叫做双曲线的中心.

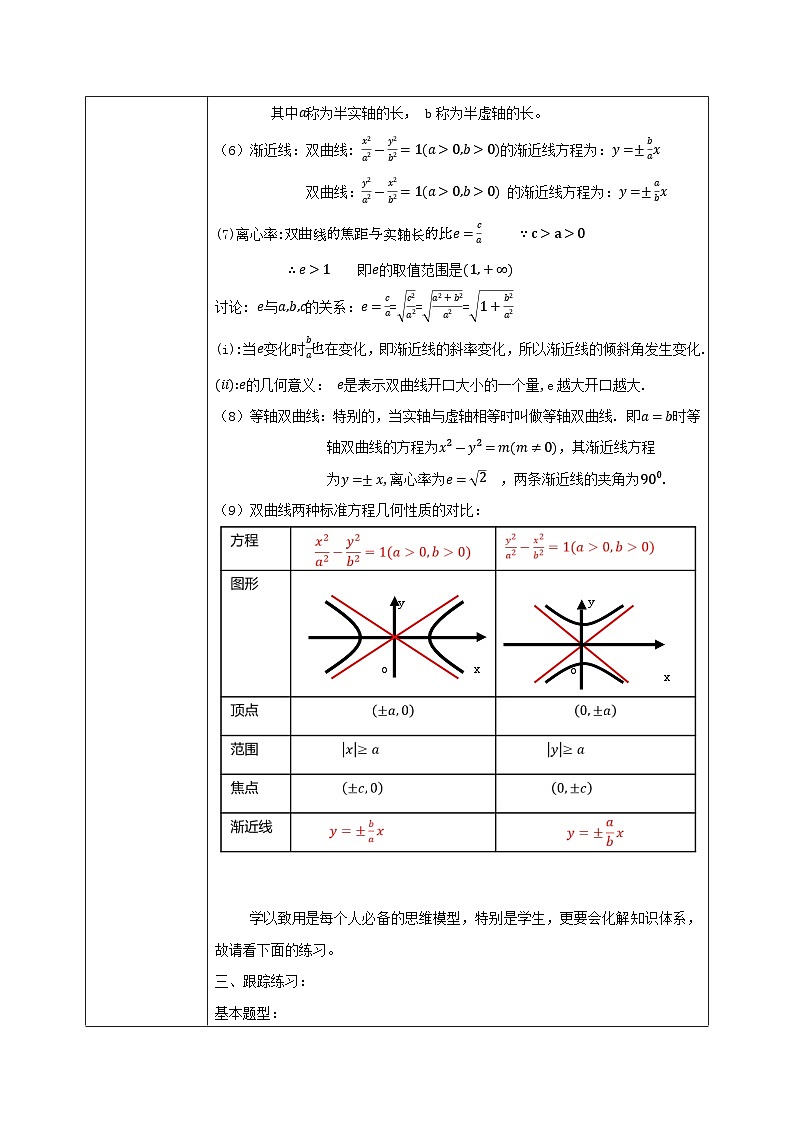
(3)顶点：双曲线与对称轴的交点，叫做双曲线顶点.

(4)实轴:线段A1A2叫做双曲线的实轴，实轴的长为，

(5)虚轴：线段B1B2叫做双曲线的虚轴,虚轴的长为,

其中称为半实轴的长， b称为半虚轴的长。  

（6）渐近线：双曲线: 的渐近线方程为：

             双曲线： 的渐近线方程为：

(7)离心率:    

              即的取值范围是

讨论: 与的关系：===

(i):当变化时在变化，即渐近线的斜率变化，所以渐近线的倾斜角发生变化.

的几何意义： 是表示双曲线开口大小的一个量,e越大开口越大.

（8）等轴双曲线：特别的，当实轴与虚轴相等时叫做等轴双曲线. 即时等轴双曲线的方程为，其渐近线方程

为,离心率为  ，两条渐近线的夹角为.

（9）双曲线两种标准方程几何性质的对比：

 学以致用是每个人必备的思维模型，特别是学生，更要会化解知识体系，故请看下面的练习。

三、跟踪练习：

基本题型：

1.求双曲线的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程。

 提示：把方程先化为标准方程.

解：双曲线方程的标准形式为：

    41

    实半轴长为4，虚半轴长为5     焦点坐标为

    渐近线方程是      离心率

2.渐近线方程为的双曲线的离心率是（       ）

解：等轴双曲线的渐近线方程为     

答案：

3.双曲线的离心率为，则双曲线的两条渐近线的夹角是（  ）

 解：双曲线的离心率为时，其渐近线方程为

    两条渐近线的夹角是.

答案：

拓展和提升本节课的数学知识和思维方法是数学学习中必不可少的一个重要环节，请学习下一个环节。

四、课堂互动：

互动一：

1.若双曲线的渐近线方程是 它是一个焦点是，则该双曲线的方程是（      ）

 解：由焦点是     得  且焦点在轴上

       渐近线方程为     

              双曲线方程为

互动二：

2.，离心率是程，并求出它的渐近线和焦点坐标.

  解: 由已知得

      =

      渐近线方程是：=

      焦点坐标是：

互动三：

3.

提示：与双曲线 有共同渐近线的双曲线方程可设为：

解：设所求双曲线的方程为

    在双曲线上                解得

    所求双曲线的方程为      即

数学核心素养价值观的形成是当今数学课改中必不可少的，请回答下列问题

五、素养形成  

1.若双曲线的离心率为，则(    )

解：==        解之，得

 答案：：

2.双曲线的一条渐近线的倾斜角为则双曲线的离心率为（         ）

解：=       

   ===

答案：

及时总结，归纳概括，是学习中必须学会的思维模式，进一步提升和拓展，请看：

六、课堂总结：

1.知识小结：（1）双曲线的几何性质----范围、对称性、顶点、焦点、离心率、渐近线、实轴、虚轴.

             (2)等轴双曲线的性质.

             (3)与双曲线 有共同渐近线的双曲线方程可设为：

2.解题技巧:（1）灵活应用已知条件解与双曲线的几何性质有关的题型；

（2）数形结合思想的巧妙应用.

课后作业

课本P124：   练习   1、2、3、4.

课本P127:    习题3.2       3、4、6、8.

板书设计

1.双曲线的几何性质：                          课堂互动:1.

2.等轴双曲线的性质：                                   2.

跟踪练习：1.                                           3..                   

          2                                  素养训练：1..                              

3                                            2.

教学反思

1.要正确灵活的应用已知条件解决有关双曲线的几何性质的数学问题。

2.数形结合思想要加强训练。

3.转化与化归思想的渗透与应用。