初中数学浙教版九年级上册第1章 二次函数1.4 二次函数的应用教学设计及反思

这是一份初中数学浙教版九年级上册第1章 二次函数1.4 二次函数的应用教学设计及反思，共5页。
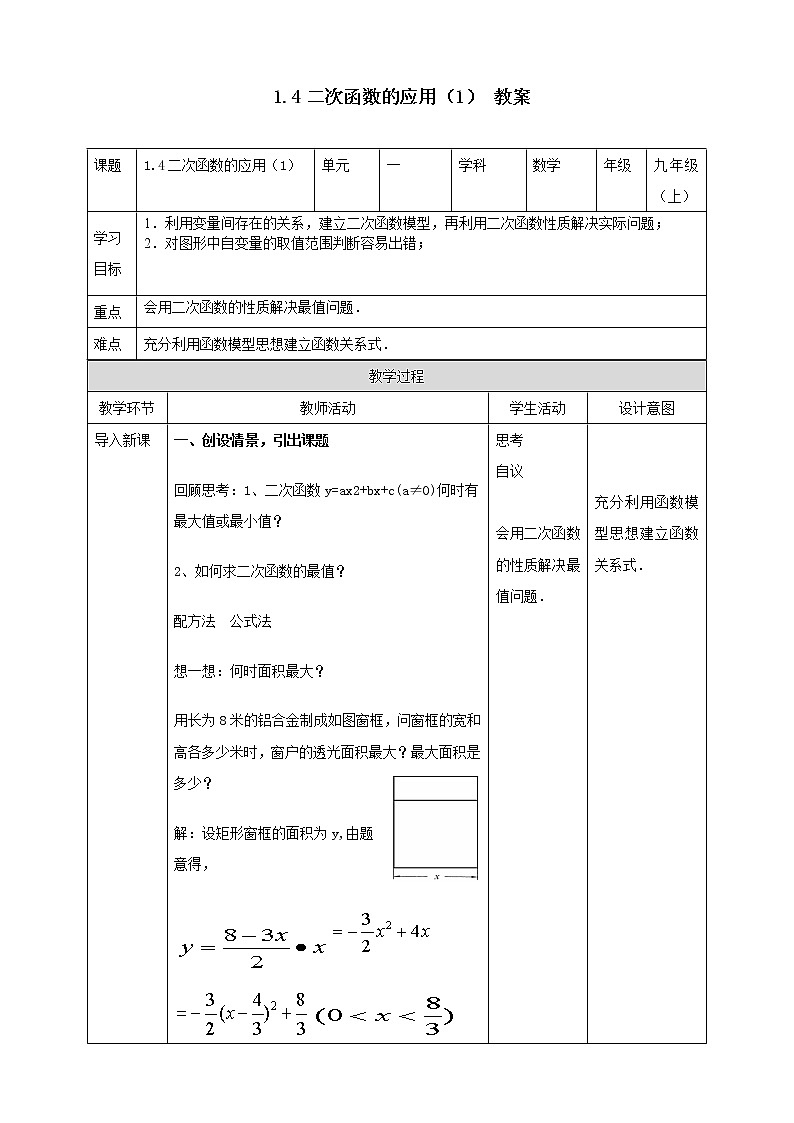
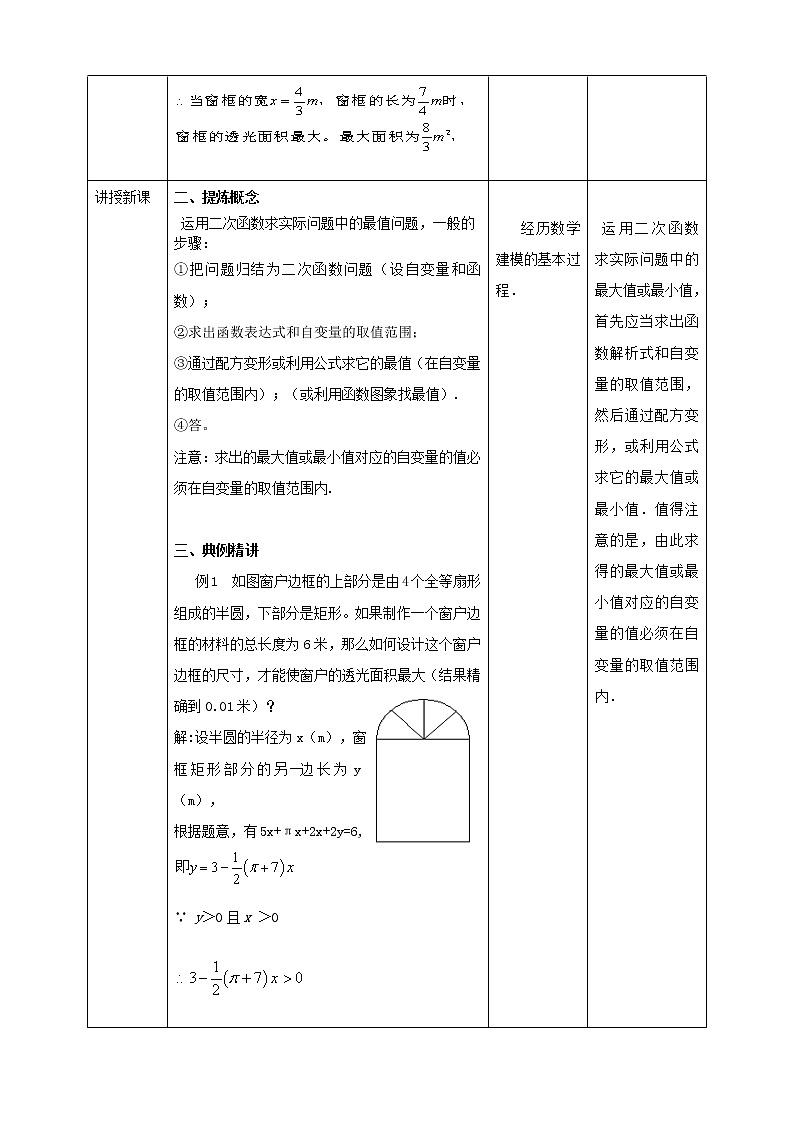
 1.4二次函数的应用（1） 教案 课题 1.4二次函数的应用（1）单元一学科数学年级九年级（上）学习目标1．利用变量间存在的关系，建立二次函数模型，再利用二次函数性质解决实际问题；2．对图形中自变量的取值范围判断容易出错；  重点会用二次函数的性质解决最值问题．难点充分利用函数模型思想建立函数关系式． 教学过程教学环节教师活动学生活动设计意图导入新课一、创设情景，引出课题回顾思考：1、二次函数y=ax2+bx+c(a≠0)何时有最大值或最小值？2、如何求二次函数的最值？配方法  公式法想一想：何时面积最大？ 用长为8米的铝合金制成如图窗框，问窗框的宽和高各多少米时，窗户的透光面积最大？最大面积是多少？解：设矩形窗框的面积为y,由题意得，思考自议 会用二次函数的性质解决最值问题．   充分利用函数模型思想建立函数关系式．讲授新课二、提炼概念 运用二次函数求实际问题中的最值问题，一般的步骤：①把问题归结为二次函数问题（设自变量和函数）；②求出函数表达式和自变量的取值范围；③通过配方变形或利用公式求它的最值（在自变量的取值范围内）；（或利用函数图象找最值）.④答。注意：求出的最大值或最小值对应的自变量的值必须在自变量的取值范围内. 三、典例精讲   例1  如图窗户边框的上部分是由4个全等扇形组成的半圆，下部分是矩形。如果制作一个窗户边框的材料的总长度为6米，那么如何设计这个窗户边框的尺寸，才能使窗户的透光面积最大（结果精确到0.01米）？解:设半圆的半径为x（m），窗框矩形部分的另一边长为y（m），根据题意，有5x+πx+2x+2y=6,∵ y＞0且x ＞0则：0＜x＜（确定自变量取值范围）此时y≈1.23答：当窗户半圆的半径约为0.35m，矩形窗框的一边长约为1.23m时，窗户的透光面积最大，最大值为1.05m2。  经历数学建模的基本过程．       运用二次函数求实际问题中的最大值或最小值，首先应当求出函数解析式和自变量的取值范围，然后通过配方变形，或利用公式求它的最大值或最小值．值得注意的是，由此求得的最大值或最小值对应的自变量的值必须在自变量的取值范围内．    课堂检测四、巩固训练1.小敏用一根长为8cm的细铁丝围成矩形，则矩形的最大面积是（     ）A. 4cm2           B. 8cm2         C. 16cm2       D. 32cm2 答案：A2.已知二次函数的图象(0≤x≤)如图．关于该函数在所给自变量的取值范围内，下列说法正确的是（    ）A．有最大值2，无最小值．B．有最大值2，有最小值1.5．C．有最大值2，有最小值－2．D．有最大值1.5，有最小值－2答案：C     3．某建筑物的窗户如图所示,它的上半部是半圆,下半部是矩形,制造窗框的材料总长(图中所有的黑线的长度和)为15m.当x等于多少时,窗户通过的光线最多(结果精确到0.01m)?此时,窗户的面积是多少?答案：解：由4y+7x+πx=15.得窗户面积S=    =当x=1.07m时，窗户通过的光线最多，此时窗户的面积是4.如图，在一面靠墙的空地上用长为24米的篱笆，围成中间隔有二道篱笆的长方形花圃，设花圃的宽AB为x米，面积为S平方米。(1)求S与x的函数关系式及自变量的取值范围；(2)当x取何值时所围成的花圃面积最大，最大值是多少？(3)若墙的最大可用长度为8米，则求围成花圃的最大面积.   解：(1) ∵ AB为x米、篱笆长为24米     ∴ 花圃宽为（24－4x）米∴ S＝x（24－4x）         ＝－4x2＋24 x   （0<x<6）(2)当x＝ 时，S最大值＝ ＝36（平方米）(3) ∵墙的可用长度为8米   ∴ 0<24－4x ≤6    4≤x<6∴当x＝4cm时，S最大值＝32 平方米    课堂小结 用二次函数求实际问题中的最大值或最小值方法：运用二次函数求实际问题的最大值或最小值，首先应当求出函数解析式和自变量的取值范围，然后通过配方变形，或利用公式求它的最大值或最小值．注意：求得的最大值或最小值对应的自变量的值必须在自变量的取值范围内．