




初中数学浙教版九年级上册3.2 图形的旋转说课课件ppt
展开
这是一份初中数学浙教版九年级上册3.2 图形的旋转说课课件ppt,共26页。PPT课件主要包含了新知导入,情境引入,合作学习,提炼概念,怎样来描述旋转呢,旋转中心,旋转角,旋转方向,必须明确,典例精讲等内容,欢迎下载使用。
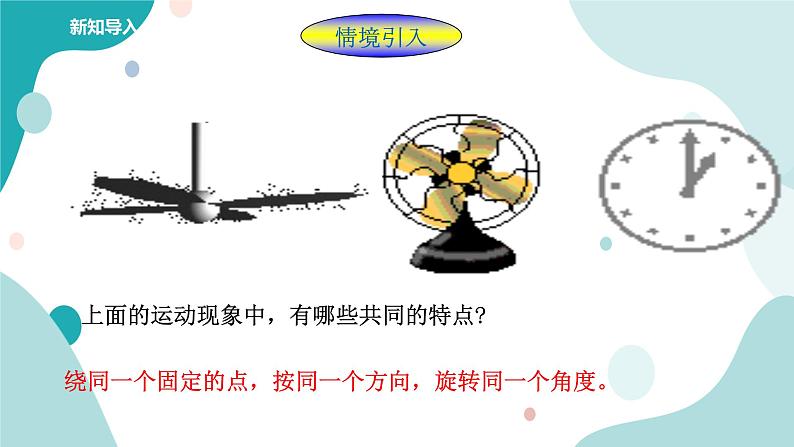
上面的运动现象中,有哪些共同的特点?
绕同一个固定的点,按同一个方向,旋转同一个角度。
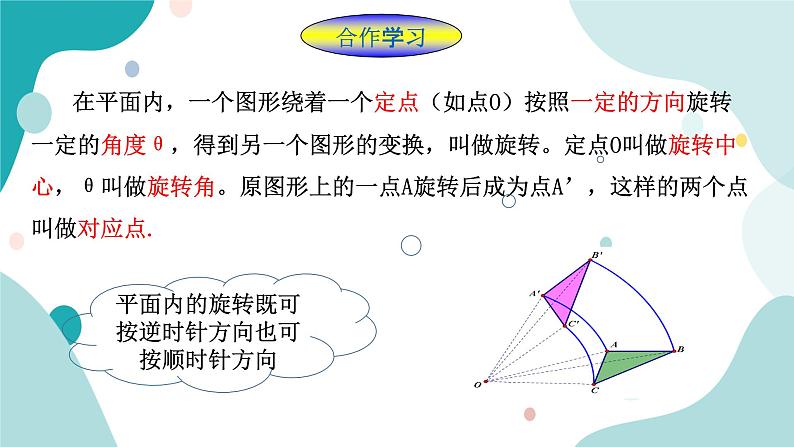
在平面内,一个图形绕着一个定点(如点O)按照一定的方向旋转一定的角度θ,得到另一个图形的变换,叫做旋转。定点O叫做旋转中心,θ叫做旋转角。原图形上的一点A旋转后成为点A’,这样的两个点叫做对应点.
平面内的旋转既可按逆时针方向也可按顺时针方向
1.下图是风车风轮中的两张叶片,叶片B能由叶片A轴对称变换得到吗?2.你有什么办法使这两张叶片A和B重合呢?
旋转:绕点O顺时针旋转900
确定一个图形的旋转时,
温馨提示:①旋转的范围是“平面内”,其中“旋转中心,旋转方向,旋转角度”称之为旋转的三要素;②旋转变换同样属于全等变换.
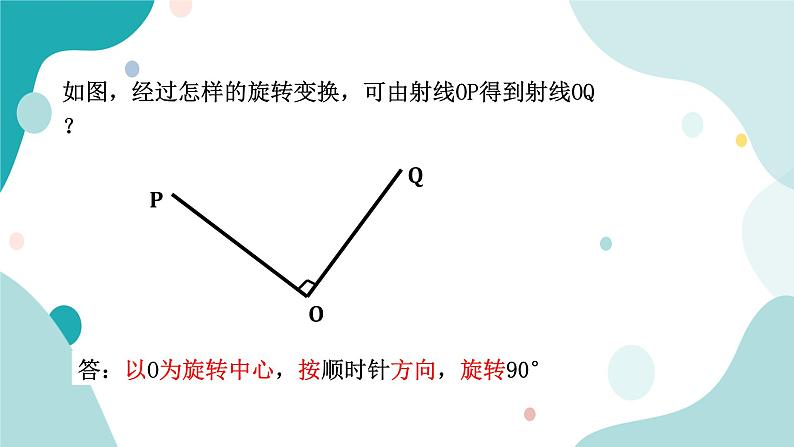
答:以O为旋转中心,按顺时针方向,旋转90°
如图,经过怎样的旋转变换,可由射线OP得到射线OQ?
如图,以点O为旋转中心,将点A按逆时针方向旋转90°,作出旋转变换后的像.
如图:点O是线段AB外一点,以点O为旋转中心,将线段AB按逆时针方向旋转100°,作出旋转变换后的像.
例1、如图,O是△ABC外一点.以点O为旋转中心,将△ABC按逆时针方向旋转80°,作出经旋转后的图形.
1. 以O为旋转中心,分别把点A, B, C按逆时针方向旋转80°,得到点A’, B’, C’.
2. 连结A’B’, B’C’, C’A’, △A’B’C’就是所求作的经旋转后的图形.
1.在图形的旋转过程中,哪些发生了改变?哪些没有发生改变?
2.分别连结对应点A、A/与旋转中心O,量一量线段OA与线段OA/,它们有什么关系?任意找一对对应点,量一下对应点到旋转中心的距离,你能发现什么规律?
3.量一下∠AOA/的度数,再任意找几对对应点,分别量一下对应点与旋转中心所连线段的夹角的度数,你又能发现什么规律?
旋转前、后的图形全等;
对应点到旋转中心的距离相等;
每一对对应点与旋转中心的连线所成的角彼此相等
是不是所有图形的旋转变换都存在:对应点到旋转中心的距离相等,对应点与旋转中心连线所成的角度等于旋转的角度?一般地,图形的旋转变换有下面的性质:一、旋转变换不改变图形的形状和大小.二、对应点到旋转中心的距离相等.三、对应点与旋转中心连线所成的角度等于旋转的角度.
平移: .
旋转: .
平移、轴对称和旋转的异同:
都是一种图形运动,运动前后不改变图形的形状和大小,只改变位置,因而也叫做图形的全等变换.
轴对称: .
例2 如图, 矩形AB’C’D’是矩形ABCD以点A为旋转中心,按逆时针方向旋转90°所得的图形.求证:对角线BD与对角线B’D’所在的直线互相垂直.
证明 如图,线段D'B'由对角线DB经旋转得到,延长D'B',交DB于点E.
又∵∠D'AD=90°(一对对应点与旋转中心连线所成的角度等于旋转的角度),
在矩形ABCD中,∠BAD=90°,
∴点D',A,B在同一条直线上.
∵Rt△D'AB'≌Rt△DAB(图形经过旋转所得的图形和原图形全等),
∴∠AD'B'+∠ADB=∠ADB+∠ABD=90°,
∴∠D'EB=180°-(∠AD'B'+∠ABD)=180°-90°=90°,即BD⊥B'D'.
1.一个图形无论经过平移还是旋转,有以下说法:①对应线段平行;②对应线段相等;③对应角相等;④图形的形状和大小都没有发生变化.其中正确的是( )A.①②③ B.①②④C.①③④ D.②③④
2.如图所示,∠AOB=90°,∠B=30°,△A′OB′可以看作是由△AOB绕点O逆时针旋转α角度得到的.若点A′在AB上,则旋转角α的大小可以是 ( )
A.30° B.45°C.60° D.90°
【解析】∵∠AOB=90°,∠B=30°,∴∠A=60°.∵△A′OB′可以看作是由△AOB绕点O逆时针旋转α角度得到的,∴OA=OA′.∴△OAA′是等边三角形.∴∠AOA′=60°,即旋转角α的大小可以是60°.
3.如图所示,两个全等的正方形ABCD与CDEF,旋转正方形ABCD能和正方形CDEF重合,则可以作为旋转中心的点有______个.
【解析】①以C为旋转中心,把正方形ABCD顺时针旋转90°,可得到正方形CDEF;②以D为旋转中心,把正方形ABCD逆时针旋转90°,可得到正方形CDEF;③以CD的中点为旋转中心,把正方形ABCD旋转180°,可得到正方形CDEF.综上所述,可以作为旋转中心的点有3个;
4. 如图所示,已知四边形ABCD绕点O顺时针旋转一定角度后,使得点A落在点A′处,试作出旋转后的图形.
解:图略.作法:(1)连结OA,OA′.(2)连结OB,OC,OD,分别以OB,OC,OD为始边,点O为顶点顺时针作∠BOB′,∠COC′,∠DOD′,并使得∠BOB′=∠COC′=∠DOD′=∠AOA′,OB′=OB,OC′=OC,OD′=OD.(3)顺次连结A′,B′,C′,D′四点.则四边形A′B′C′D′就是所要作的图形.
【点悟】旋转作图的依据是图形上每一点都绕旋转中心沿相同的方向转动了相同的角度,对应点到旋转中心的距离相等,这是旋转的基本规律,也是我们作图的依据,对于旋转作图,应先确定图形的“关键点”,以局部带动整体进行旋转.
5. 如图所示,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.
(1)线段OA1的长是______.∠AOB1的度数是________;(2)连结AA1,求证:四边形OAA1B1是平行四边形;(3)求四边形OAA1B1的面积.
解:(1)OA1=OA=6,∠AOB1=∠A1OB1+∠AOA=45°+90°=135°(2)证明:∵∠AOA1=∠OA1B1=90°,∴OA∥A1B1,又OA=AB=A1B1,∴四边形OAA1B1是平行四边形;(3)四边形OAA1B1的面积=OA·OA1=6×6=36.
【点悟】(1)旋转前、后的图形全等,对应角、对应边相等;(2)对应点与旋转中心连线所成的夹角等于旋转角.
1.旋转的概念旋转:一般地,一个图形变为另一个图形,在运动过程中原图形上所有的点都绕一个固定的点,按同一个方向,转动同一个角度,这样图形运动叫做图形的旋转.固定的点叫做_____________,转动的角叫做___________.
注意:(1)旋转中心是点,而不是直线,如生活中的开门、关门是绕轴旋转一定的角度.不属于我们研究的绕定点旋转;(2)经过旋转后,图形上任意一对对应点与旋转中心的连线所成的角都是旋转角.
2.旋转的性质性质:(1)对应到旋转中心的距离________;(2)对应点与旋转中心连线所成的夹角等于___________;(3)旋转前后的图形_________.3.作旋转图形的一般步骤步骤:(1)明确三个条件:旋转中心,旋转方向,旋转角度;(2)确定关键点,作出关键点旋转后的对应点;(3)顺次连结对应点.
相关课件
这是一份初中数学浙教版九年级上册第3章 圆的基本性质3.2 图形的旋转授课ppt课件,共17页。PPT课件主要包含了观察与思考,一个固定的点,同一个方向,同一个角度,旋转中心,旋转的方向,旋转的角度,什么是图形的旋转呢,旋转角,∠ADE等内容,欢迎下载使用。
这是一份浙教版九年级上册3.2 图形的旋转优质课ppt课件,文件包含浙教版数学九上32图形的旋转课件pptx、浙教版数学九上32图形的旋转学案doc、浙教版数学九上32图形的旋转教案doc等3份课件配套教学资源,其中PPT共27页, 欢迎下载使用。
这是一份初中数学浙教版九年级上册3.2 图形的旋转授课ppt课件,共15页。PPT课件主要包含了活动一,直观感知形成概念,旋转中心,旋转方向,对应点,∠pop′,旋转角,顺时针,巩固概念与性质等内容,欢迎下载使用。









