新高考数学二轮专题《立体几何》第8讲 立体几何范围与最值问题（2份打包，解析版+原卷版）

这是一份新高考数学二轮专题《立体几何》第8讲 立体几何范围与最值问题（2份打包，解析版+原卷版），文件包含新高考数学二轮专题《立体几何》第8讲立体几何范围与最值问题解析版doc、新高考数学二轮专题《立体几何》第8讲立体几何范围与最值问题原卷版doc等2份试卷配套教学资源，其中试卷共48页， 欢迎下载使用。
第8讲 立体几何范围与最值问题
一．选择题（共34小题）
1．在空间中有一棱长为的正四面体，其俯视图的面积的最大值为　　
A． B． C． D．
【解答】解：由题意当线段相对的侧棱与投影面平行时投影最大，此时投影是关于线段对称的两个等腰三角形，
由于正四面体的棱长都是1，故投影面积为．
故选：．
2．已知三棱锥的四个顶点均在同一个球面上，底面满足，，若该三棱锥体积的最大值为，则其外接球的半径为　　
A．1 B．2 C．3 D．
【解答】解：如图所示，由，，
可得，，
，．
设的外接圆的半径为，，．
当平面时，该三棱锥取得体积的最大值为
由．
解得．
所以，
解得．
故选：．

3．已知三棱锥的四个顶点在以为直径的球面上，，于，，若三棱锥的体积的最大值为，则该球的表面积为　　
A． B． C． D．
【解答】解：三棱锥的四个顶点在以为直径的球面上，
如图所示：

由于：为球体的球心，
所以：，
由于，于，，
为的中点，
所以平面，
则，
．
故：，
由于．
所以：，解得．
所以．
故选：．
4．已知球的直径，，是该球面上的两点，，则三棱锥的体积最大值是　　
A．2 B． C．4 D．
【解答】解：如图，球的直径，，是该球面上的两点，，
，，（其中为点到底面的距离），
故当最大时，的体积最大，
即当面面时，最大，
球的直径，，，
，
，即，
此时．
故选：．

5．如图，正三棱锥的侧棱长为，两侧棱、的夹角为，、分别是、上的动点，则的周长的最小值是　　

A． B． C． D．
【解答】解：三棱锥的侧面展开图，如图，
的周长的最小值为，
由于题 设知，正三棱锥的侧棱长为
所以，
故选：．

6．在正三棱锥中，，，两两垂直，，点在线段上，且，过点作该正三棱锥外接球的截面，则所得截面圆面积的最小值是　　
A． B． C． D．
【解答】解：在正三棱锥中，，，两两垂直，，
构造以，，为棱长的正方体，且该正方体棱长为，
以为原点，为轴，为轴，为轴，建立空间直角坐标系，
则该正三棱锥外接球球心为中点，半径为，
点在线段上，且，
，，，，
，
过点作该正三棱锥外接球的截面，当所得截面圆面积取最小值时截面圆的圆心为，
当所得截面圆面积取最小值时截面圆的半径为：
，
过点作该正三棱锥外接球的截面，则所得截面圆面积的最小值为．
故选：．

7．如图，在棱长为2的正方体中，点是的中点，动点在底面内（不包括边界）．若平面，则的最小值是　　

A． B． C． D．
【解答】解：如图，在上取中点，在上取中点，连接，，，
，且，，
平面，则动点的轨迹是，（不含，两点）
又平面，
则当时，取得最小值，
．
故选：．

8．在棱长为1的正方体中，点，分别是线段，（不包括端点）上的动点，且线段平行于平面，则四面体的体积的最大值是　　
A． B． C． D．
【解答】解：平面，平面，平面平面，
，
，
设到平面的距离为，则，
，
故，而，
四面体的体积，
当时取得最大值．
故选：．

9．棱长为1的正方体中，点，分别是线段，（不包括端点上的动点，且线段平行于平面，则四面体的体积的最大值是　　
A． B． C． D．
【解答】解：由题意在棱长为1的正方体中，点，分别是线段，（不包括端点）上的动点，且线段平行于平面，△△，
设，，则，到平面的距离为，
所以四面体的体积为，
当时，体积取得最大值：．
故选：．

10．若一个四棱锥底面为正方形，顶点在底面的射影为正方形的中心，且该四棱锥的体积为9，当其外接球表面积最小时，它的高为　　
A．3 B． C． D．
【解答】解：设底面边长，棱锥的高，
，
，
正四棱锥内接于球，
在直线上，设球半径为，
（1）若在线段上，如图一，则，
（2）若在在线段的延长线上，如图二，则，
平面，
是直角三角形，
，
，，
，或
，
即．
当且仅当取等号，
即时取得最小值．
故选：．


11．已知正四棱锥中，，那么当该棱锥的体积最大时，它的高为　　
A．1 B． C．2 D．3
【解答】解：设底面边长为，则高，所以体积，
设，则，当取最值时，，解得或时，当时，体积最大，
此时，
故选：．
12．已知在半径为2的球面上有、、、四点，若，则四面体的体积的最大值为　　
A． B． C． D．
【解答】解：过作平面，使平面，交于，设点到的距离为，
则有，
当直径通过与的中点连线时，，故．
故选：．

13．如图所示，圆形纸片的圆心为，半径为，该纸片上的正方形的中心为．，，，为圆上的点，，，，分别是以，，，为底边的等腰三角形．沿虚线剪开后，分别以，，，为折痕折起，，，，使得，，，重合，得到四棱锥．当正方形的边长变化时，所得四棱锥体积（单位：的最大值为　　

A． B． C． D．
【解答】解：沿虚线剪开后，分别以，，，为折痕折起，，，，
使得，，，重合，得到四棱锥，
由题意得，，
，
所得四棱锥体积（单位：
，
构造函数（a），则（a），
当（a）时，，在内递增，在其他定义域内递减，
当时，取得最大值，也就是取得最大值，
将代入，得：
所得四棱锥体积（单位：的最大值为．
故选：．

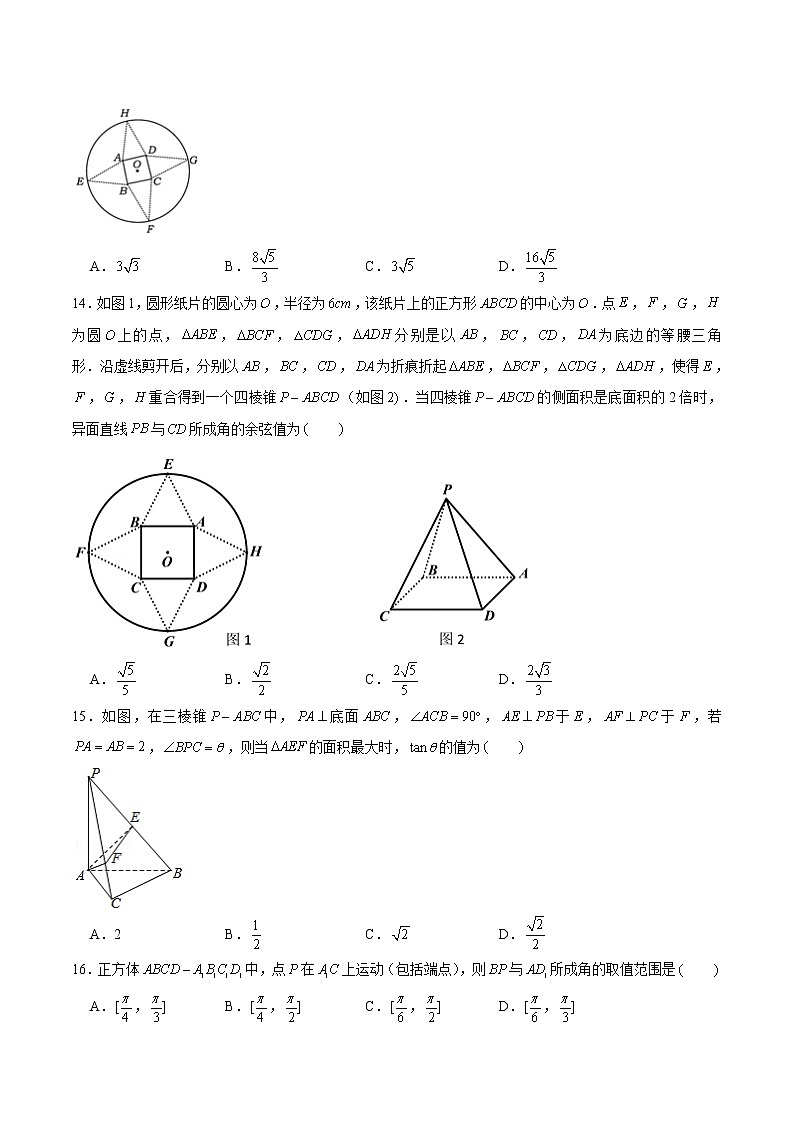
14．如图1，圆形纸片的圆心为，半径为，该纸片上的正方形的中心为．点，，，为圆上的点，，，，分别是以，，，为底边的等腰三角形．沿虚线剪开后，分别以，，，为折痕折起，，，，使得，，，重合得到一个四棱锥（如图．当四棱锥的侧面积是底面积的2倍时，异面直线与所成角的余弦值为　　

A． B． C． D．
【解答】解：如图，连接交于点，设正方形的边长为．
则，，
由四棱锥的侧面积是底面积的2倍，
可得，
解得．
即，，，
所以，
所以在四棱锥中，，
因为，所以即为异面直线与所成的角，
所以，
即异面直线与所成角的余弦值为．
故选：．

15．如图，在三棱锥中，底面，，于，于，若，，则当的面积最大时，的值为　　

A．2 B． C． D．
【解答】解：在中，，，
，，．
底面，得，，
平面，可得
，，平面
平面，
且，面，
结合平面，可得．
中，，可得，
平面，平面．．
中，，

当，即时，有最大值为
故选：．
16．正方体中，点在上运动（包括端点），则与所成角的取值范围是　　
A．， B．， C．， D．，
【解答】解：设与所成角为．
如图所示，不妨设．
则，0，，，0，，，1，，，0，，
，0，，，0，，，1，．
设，则，，．．

，
．
故选：．

17．已知与是四面体中相互垂直的棱，若，且，则四面体的体积的最大值是　　
A． B． C．18 D．36
【解答】解：过作，垂足为，连接，
，，，
平面，
．
又，平面，
，，
取的中点，则，
，
当最大时，棱锥的体积取得最大值．
又，故当最大时，棱锥体积最大，
，，当时，取得最大值，
此时，
棱锥的体积最大值为．
故选：．

18．在直四棱柱中，底面为菱形，，分别是，的中点，为的中点且，则的面积的最大值为　　
A． B．3 C． D．
【解答】解：连接交于，
底面是菱形，，
以，，为坐标轴建立空间直角坐标系，
设，，棱柱的高为，
则，0，，，，，，，，，，．
，，，，，，
，
到直线的距离，
．当且仅当即时取等号．
故选：．

19．在正四棱锥中，平面于，，底面边长为，点，分别在线段，上移动，则两点的最短距离为　　
A． B． C．2 D．1
【解答】解：如图，由于点、分别在线段、上移动，先让点在上固定，在上移动，当最小时，最小．过作，在中，，
在上运动，且当运动到点时，最小，又等于的长为，也就是异面直线和的公垂线段的长，
故选：．

20．已知二面角为，动点，分别在面，内，到的距离为，到的距离为，则，两点之间距离最小值为　　
A． B．2 C．4 D．
【解答】解：如图
分别作于，于，于，于，
连，则，，，

又
当且仅当，即点与点重合时取最小值．
故选：．

21．如果，与是夹在平面与之间的两条线段，且，直线与平面所成的角为，那么线段长的取值范围是　　
A．， B．， C． D．，
【解答】解：由题意，在平面，当和重合时，、在平面上，、、构成直角三角形，一内角为，此时最小为；
当与两个面近似平行时，达到无限长．
线段长的取值范围为，．
故选：．
22．正三棱柱中，各棱长均为2，为中点，为的中点，则在棱柱的表面上从点到点的最短距离是　　
A． B． C． D．
【解答】解：沿着棱将棱柱的侧面展开，故小虫爬行的最短距离为，
故选：．
23．在长方体中，，，点为的中点，点为对角线上的动点，点为底面上的动点（点、可以重合），则的最小值为　　
A． B． C． D．1
【解答】解：由题意，要求的最小值，就是到底面的距离的最小值与的最小值之和，是在底面上的射影距离最小，展开三角形与三角形，在同一个平面上，如图，易知，，可知时，的最小，最小值为：．
故选：．

24．在中，，，，点在斜边上，以为棱把它折成直二面角，折叠后的最小值为　　
A． B． C． D．3
【解答】解：设，则，
作于，于，
于是，，
，
是直二面角，，，
与成角，

．
当，即是的平分线时，
有最小值，最小值是．
故选：．

25．在平面四边形中，，，且，现将沿着对角线翻折成△，则在△折起至转到平面内的过程中，直线与平面所成的最大角为　　
A． B． C． D．
【解答】解：如图，平面四边形中，
连结，，交于点，
，
，且，
，，
，
，
．
将沿着对角线翻折成△，
当与以为圆心，为半径的圆相切时，
直线与平面所成角最大，
此时，△中，，，
，
与平面所成的最大角为．
故选：．

26．已知三棱锥中，，且与平面成角．当的值取到最大值时，二面角的大小为　　
A． B． C． D．
【解答】解：过作平面，连接并延长交，于，连接，
则是在底面上的射影，
则，
，，
平面，即，
则是二面角的平面角，
则，
要使的值取到最大值，则取得最大，
由正弦定理得，
当取得最大值，即当时取最大值．
此时，
故选：．

27．已知三棱锥的所有顶点都在表面积为的球的球面上，为球的直径，当三棱锥的体积最大时，设二面角的大小为，则　　
A． B． C． D．
【解答】解：如图所示：由已知得球的半径为2，
为球的直径，当三棱锥的体积最大时，为等腰直角三角形，在面上的射影为圆心，
过圆心作于，连结，则为二面角的平面角，
在△中，，，，．
故选：．

28．在正方体中，，是底面正方形内一点，是中点若，与底面所成角相等，则最大值为　　

A． B． C． D．
【解答】解：连接，，则，分别为和与平面所成的角，
和与平面所成的角相等，
，
，
；
又为的中点，
，
以为坐标原点，，分别为，轴，建立平面直角坐标系，
设正方体的棱长为1，则，
设，则，
即，
则的轨迹为圆被正方形所截的一段圆弧，
则当位于圆弧与的交点位置时，最小为．
此时有最大值为．
故选：．

29．已知的顶点平面，点，在平面同侧，且，，若，与所成角分别为，，则线段长度的取值范围为　　
A．， B．， C．， D．，
【解答】解：分别过，作底面的垂线，垂足分别为，．
由已知可得，，，，．
如图，当，所在平面与垂直，且，在底面上的射影，在点同侧时长度最小，
当，所在平面与垂直，且，在底面上的射影，在点两侧时长度最大．

过作，垂足为，则，
的最小值为，最大值为，
的最小值为，最大值为．
线段长度的取值范围为，
故选：．
30．如图，空间直角坐标系中，正三角形的顶点，分别在平面和轴上移动．若，则点到原点的最远距离为　　

A． B．2 C． D．3
【解答】解：连结，取的中点，连结、，根据题意可得
中，斜边，，
又正的边长为2，
，
对图形加以观察，当，分别在平面和轴上移动时，
可得当、、三点共线时，到原点的距离最远，且这最远距离等于
故选：．

31．棱长为2的正方体在空间直角坐标系中移动，但保持点、分别在轴、轴上移动，则点到原点的最远距离为　　
A． B． C．5 D．4
【解答】解：由题意可知，与和在同一个平面时，到的距离比较大，如图：设，则坐标为，


，其中，
显然，
故选：．

32．如图在棱长为2的正方体中为的中点，点在线段上，点到直线的距离的最小值为　　

A． B． C． D．
【解答】解：如图所示，取的中点，连接，，
，底面，四边形是矩形．
，
又平面，平面，平面．
直线上任一点到平面的距离是两条异面直线与的距离．
过点作，
平面平面．
平面．
过点作交于点，则．
取，连接，则四边形是矩形．
可得平面，
在△中，，得．
点到直线的距离的最小值为．
故选：．

33．若点，，是半径为2的球面上三点，且，则球心到平面的距离最大值为　　
A． B． C． D．
【解答】解：因为当截面是以为直径的圆时，
球心到过、两点的平面的距离最大．
设截面圆的圆心为，球心为，
则△是以的直角三角形，
且，，球心到截面的距离．
所以：截面圆半径为1，球心到截面的距离为：．
故选：．
34．二面角的平面角为，在面内，于，在平面内，于，，，是棱上的一个动点，则的最小值为　　
A．6 B． C． D．5
【解答】解：将二面角平摊开来，即为图形
当、、在一条直线时的最小值，最小值即为对角线
而，
故．
故选：．

二．多选题（共1小题）
35．已知三棱锥中，，，，，则　　
A．三棱锥的外接球的体积为
B．三棱锥的外接球的体积为
C．三棱锥的体积的最大值为
D．三棱锥的体积的最大值为
【解答】解：如图，，，，
，
，
，
的中点为外接球球心，
故半径为1，
体积为，
当面与面相互垂直时，点到面的距离最大，
故此时三棱锥的体积最大，此时高为；
其最大值为：．
故选：．

三．填空题（共14小题）
36．已知三棱锥满足，则该三棱锥体积的最大值为　　．
【解答】解：如图，，

取中点，连接，，可得，，
平面，设，
，
当平面平面时，三棱锥体积最大，
此时，
，
当时，，当时，，
．
故答案为：．
37．设，，，是同一个半径为4的球的球面上四点，为等边三角形且其面积为，则三棱锥体积的最大值为　　．
【解答】解：设，，，是同一个半径为4的球的球面上四点，为等边三角形且其面积为，
，解得，
球心为，三角形 的外心为，显然在的延长线与球的交点如图：
，，
则三棱锥高的最大值为：6，
则三棱锥体积的最大值为：．
故答案为：．

38．点在正方体的侧面及其边界上运动，并保持，若正方体边长为2，则的取值范围是　，　．
【解答】解：点在正方体的侧面及其边界上运动，并保持，可知：平面与直线垂直，所以在线段上，正方体的棱长为2，所以的最小值为，最大值为2．
则的取值范围是，．
故答案为：，．

39．如图，在棱长为2的正方体中，点是中点，动点在底面内（不包括边界），使四面体体积为，则的最小值是　　．

【解答】解：由题意，，
故．
将底面建立一个如下图所示的平面直角坐标系：

，，
在中，．
根据题意，动点为底面内任意一点，设，交于点，则
．
解得．
动点的轨迹为与直线距离为的一条平行线．
又，，，
直线，即．
点到直线距离．
点到到点的最小距离．
点到到点的最小值为．
故答案为：．
40．棱长为1的正方体如图所示，，分别为直线，上的动点，则线段长度的最小值为　　．

【解答】解：棱长为1的正方体如图所示，，分别为直线，上的动点，
线段长度的最小值是异面直线与间的距离，
以为原点，为轴，为轴，为轴，建立空间直角坐标系，
，0，，，1，，，1，，，1，，
，1，，，1，，
线段长度的最小值：


．
故答案为：．

41．如图，在棱长为1的正方体中，点是线段上的动点．当在平面，，上的正投影都为三角形时，将它们的面积分别记为，，．
当时，　　（填“”或“”或“” ；
的最大值为　　．

【解答】解：设在平面和平面上的投影分别为，，
则、到平面的距离相等，即，
，，
．
设在底面的投影为，则在上，
设且，
则，
，，
，，
，
当时，取得最大值．
故答案为：，．

42．在棱长为1的正方体中，点是棱的中点，点是线段上的动点，点是线段上的动点，设直线与平面所成的角为，则的最大值为　　．
【解答】解：如图，不妨取为，直线在平面中，直线与平面所成的角的最大值就是二面角的大小，过作，连结，就是所求角．
正方体的棱长为1，，．
．
．
故答案为：．

43．如图，圆形纸片的圆心为，半径为，该纸片上的等边三角形的中心为．，，为圆上的点，，，分别是以，，为底边的等腰三角形．沿虚线剪开后，分别以，，为折痕折起，，，使得，，重合，得到三棱锥．当所得三棱锥体积（单位：最大时，的边长为　　．

【解答】解：由题意，连接，交于点，由题意得，，
设，则，，
三棱锥的高，
，
则，
令，，，
令，即，解得，
则（2），
，体积最大值为．
此时的边长为．
故答案为：．

44．在棱长为1的正方体中，为线段的中点，是棱上的动点，若点为线段上的动点，则的最小值为　　．

【解答】解：连接，则，点、、在平面中，
且，，，
如图1所示；
在△中，以为轴，为轴，建立平面直角坐标系，
如图2所示；
则，，；
设点关于直线的对称点为，
的方程为①，
，
直线的方程为②，
由①②组成方程组，解得，，
直线与的交点，；
所以对称点，，

故答案为：．
45．在正方体中，为棱的中点，且，点为底面所在平面上一点，若直线，与底面所成的角相等，则动点的轨迹所围成的几何图形的面积为　　．
【解答】解：如图，

设正方体的棱长为，连接，
则，解得．
连接，，可得，为直线，与底面所成的角，
由，可得，．
如图建立空间直角坐标系，在平面直角坐标系中，
，，，设，
则，
化简得：，故点的关键为圆，半径．
故所求面积为．
故答案为：．
46．如图，在棱长为2的正方体中，为的中点，点在线段上，点在线段上，则线段长的最小值为　　．

【解答】解：如图所示，取的中点，连接，，
，底面，四边形是矩形．
，
又平面，平面，平面．
直线上任一点到平面的距离是两条异面直线与的距离．
过点作，
平面平面．
平面．
过点作交于点，则．
取，连接，则四边形是矩形．
可得平面，
在△中，，得．
点到直线的距离的最小值为．
故答案为：．

47．如图，正方体的棱长为，点为的中点，在对角面上取一点，使最小，其最小值为　　．

【解答】解：取的中点，则，

故答案为：
48．已知正四面体的棱长为1，为的中点，在线段上，则的最小值为　　．
【解答】解：由于各棱长均为1的四面体是正四面体
把平面及平面以为折线展平，三角形是正三角形的一半
，，，，
故在平面中，连接，与相交于点，则为最短距离，
在三角形中，根据余弦定理，
，，
，
．
故答案为：．


49．在棱长均为1的正四面体中，为的中点，为上的动点，则的最小值为　　．
【解答】解：如图，

记，在中，，，
可得，．
将绕旋转，使在平面内，此时在处．
连接，，则所求最小值即为的长．
，


．
的最小值为．
故答案为：．
四．解答题（共1小题）
50．如图所示，正三棱锥的底面边长为，侧棱长为，点，分别为、上的动点，求截面周长的最小值和这时点，的位置

【解答】解：把正三棱锥的侧面展开，
两点间的连接线即是截面周长的最小值．
，
△，
，
其中，’ ．

又，
，其中，，，
，
截面周长最小值是’ ，、两点分别满足．