

2022年通用物理中考微专题-压强-9-3 切割体的压强(含答案)
展开微专题9-3 切割体的压强
知识· 解读
常用方法有:物理公式推导(定性、定量)、数学比例、极限法、分解法、赋值法等。
1、 根据题目提供的已知条件判断出两个物体原来的密度、压力、压强的大小关系:可根据 P=F/S、 P=ρgh
或ρ=m/V等判断。
2、根据要求的未知物理量,确定压强、压力的变化情况,变化量(ΔP、ΔF)。
3、结合题目找出改变(增大或减小)ΔP、ΔF的方法。
①变化的压强可以用ΔP=ΔF/S (对于柱类物体也可用ΔP=ρgΔh)
或ΔP=P1-P2等分析计算;
②变化的压力可以用ΔF=Δmg 、 ΔF=ΔPS 、 ΔF=mg/n( n为比例)
或ΔF=F1-F2等分析计算;
③柱形物体或液体的压强均可以用P=F/S 或 P=ρgh判断,要看题目提供的条件。
分析此类问题应用的知识多,综合性强,应熟练掌握质量、重力、压力、密度、压强及体积、面积等有关知识。
典例· 解读
S
P0
S
P`1
S2
P2
S4
P4
S3
P3
例1、如图所示,质地均匀的实心木块放在水平桌面上,对桌面的压强为p0。按照图中虚线对木块切割,切割后剩余部分对桌面的压强分别为p1,p2,p3,p4,请比较它们与p0大小关系。
【答案】
【解析】本题考察固体压强的切割问题。此类问题通常有两种解题思路:
思路一:根据,分别考虑压力和受力面积的变化,据此分析压强的变化。
思路二:根据柱形固体压强计算式,分析高度是否变化。
首先看横向切割,如图1所示:
方法一:根据,横向切割后,压力变小,受力面积不变,故压强变小。
方法二:木块横切后仍是柱体,利用计算式分析,剩余木块的密度不变,高度变小,
故压强变小。
再看竖直切割,如图2所示:
方法一:采用特殊值法,假设切去整体的三分之一
则剩余部分对桌面的压强 即竖切前后压强不变。
方法二:木块竖直切割后仍是柱体,利用计算式分析,剩余木块的密度和高度均不变,故压强不变。
比较两种方法,发现通过计算式来分析横切或竖切问题都较为简便。
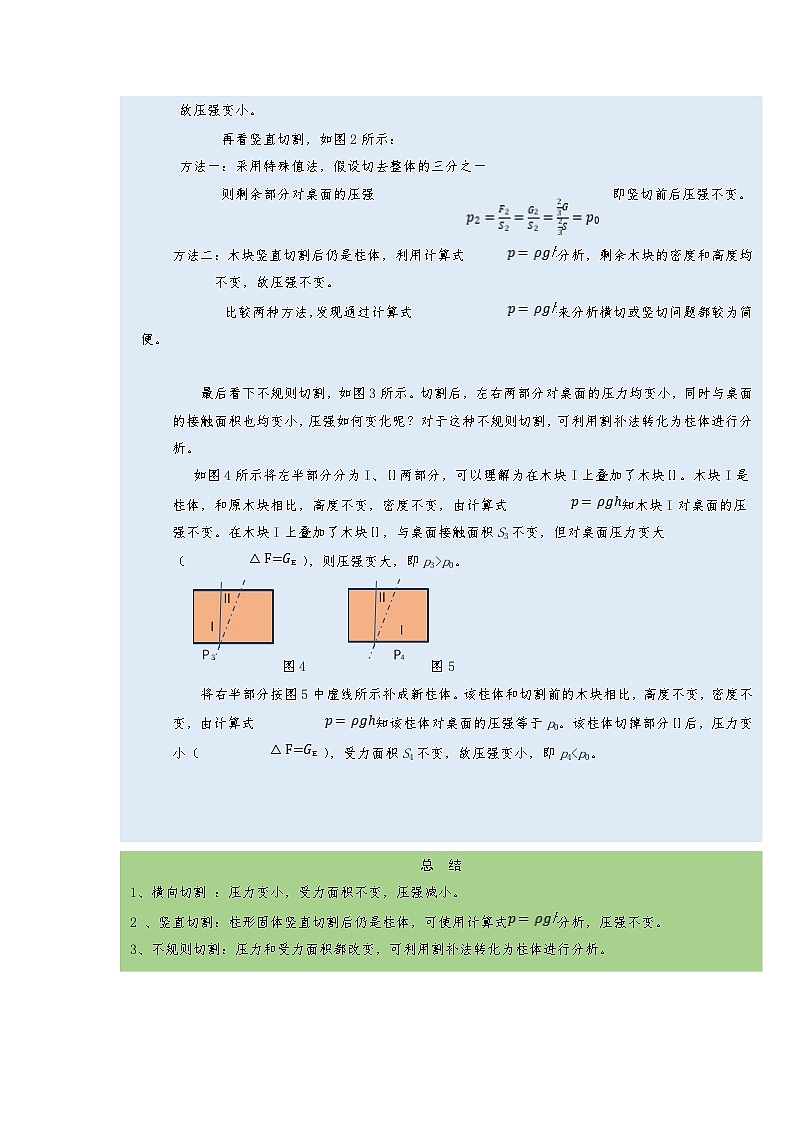
最后看下不规则切割,如图3所示。切割后,左右两部分对桌面的压力均变小,同时与桌面的接触面积也均变小,压强如何变化呢?对于这种不规则切割,可利用割补法转化为柱体进行分析。
如图4所示将左半部分分为I、Ⅱ两部分,可以理解为在木块I上叠加了木块Ⅱ。木块I是柱体,和原木块相比,高度不变,密度不变,由计算式知木块I对桌面的压强不变。在木块I上叠加了木块Ⅱ,与桌面接触面积S3不变,但对桌面压力变大(),则压强变大,即p3>p0。
图4 图5
将右半部分按图5中虚线所示补成新柱体。该柱体和切割前的木块相比,高度不变,密度不变,由计算式知该柱体对桌面的压强等于p0。该柱体切掉部分Ⅱ后,压力变小(),受力面积S4不变,故压强变小,即p4
总 结
1、横向切割 :压力变小,受力面积不变,压强减小。
2 、竖直切割:柱形固体竖直切割后仍是柱体,可使用计算式分析,压强不变。
3、不规则切割:压力和受力面积都改变,可利用割补法转化为柱体进行分析。
类型一:水平切割问题
甲
乙
例2、如图所示,甲、乙两个均匀实心正方体放在水平地面上,它们对地面的压强关系为p甲=p乙。若分别沿水平方向截去一部分后,使它们对地面的压强变为p′甲>p′乙,则( )
A.可能是截去相同的质量 B.一定是甲截去的质量小于乙的质量
C.可能是截去相同的体积 D.一定是截去相同高度
【答案】B.
【解析】本题考查切割柱体的压强问题。涉及到压强的变化量,通常采用变化量法求解:
(1)当受力面积不变时
(2)柱状物体压强问题中,当密度不变时
下面来分析本题:
未截前p甲=p乙,分别沿水平方向截去一部分后,p′甲>p′乙
所以△p甲<△p乙
由得:
即 故B正确,A错误。
再来看下选项C。截去相同的体积,质量大小关系呢?要先判断下密度关系。
由得:
图中 则
即截去相同体积,不符合我们之前的判断,C错误。
再来看D选项。一定是截去相同高度吗?分析一下:
由得:
由于 则,即一定是甲截去的高度小于乙截去的高度。D错误。
回顾整道题,主要是利用变化量法求解,注意推导过程一定要严谨!
有没有更快速的做题方法呢?有!极限法!
看下选项A,提到截去相同的质量,不妨将其中最轻的一个全部截去。我们从p甲=p乙,S甲
同样的方法也可以用于判断BCD选项。同学们自己思考下。
总 结
1、处理切割柱体的压强问题时,若面对不需要严格得出具体数值的题目,有时可以选用比较快捷的特殊值法或极限法,不过这些都不是严谨方法,偶尔使用尚可,建议同学们还是通过严格的推导来解题。
2、回顾整道题,我们发现此类题目利用变化量:、可以快速求解,但注意:任何技巧都建立在扎实的基本功之上。每个计算式都要明确是怎么推导的,不要编造公式,比如:就是错误公式。
甲
乙
例3图
例3、如图所示,甲、乙两个实心均匀正方体分别放在水平地面上,它们对地面的压强相等。若在两个正方体的上部,沿水平方向分别截去相同高度的部分,则剩余部分对水平地面的压强p以及剩余部分质量m的大小关系为 ( )
A.p甲
C.p甲>p乙 m甲>m乙 D.p甲>p乙 m甲=m乙
【答案】C.
【解析】方法一:基本公式推导
第一步先比较甲与乙密度的大小关系:
第二步比较变化的压强△P的大小关系,运用沿水平方向分别截去相同的高度,
第三步用P'=P原来-△P比较切割后压强的大小,
第四步根据P=F/S判断质量的大小,
方法二:图像法
对于所有均匀柱体水平切割问题,我们都可以把它转化为函数图像来解决。
根据
p与m成正比,m与h成正比,那么p也与h成正比,
令:原压强为p,原高度为h,水平切割后新压强为p',切割的高度为△h,则新高度为h-△h,
故有: →
可以看出p'与△h为一次函数,
作出甲乙的p'与△h一次函数, (由题干中的图可知:h1>h2)
由图像可以轻易看出p1>p2
同理,也可以做出p'与△m 的函数图像,就可以轻易得出结论
推而广之,关于均匀柱体水平横切等等问题,诸如:F与体积、质量、高度;p与体积、质量、高度都可以转化为图像来解决。
当然有很多同学认为,函数图像很难想到,写出函数关系,作出图像本身有难度,此类问题何必如此复杂,直接用极限法或者特殊值法不是更简单明了吗?
在这里我要说明两点:
①极限法或者特殊值法虽然简单,但是理解不透彻或者考虑不全面就极易犯错;
②图像法是一种重要的思想方法,以后高中会成为基本方法,对于数学较好的同学而言,此法更易理解,熟练之后一样快捷。对于以后的物理以及数学学习会很有帮助!
易错题链接(大家可以思考一下,下面两道题都能用极限法来思考吗?)
1、放在水平地面上的柱形物体,V甲>V乙,甲对地面的压力大于乙对地面的压力。在两物体上部沿水平方向切去相同的体积,则余下部分对地面的压力F甲、F乙关系是 ( )
A.F甲一定小于F乙
B.F甲可能等于F乙
C.F甲一定大于F乙
D.F甲可能大于F乙
2、放在水平地面上的柱形物体,V甲>V乙,甲对地面的压力小于乙对地面的压力。在两物体上部沿水平方向切去相同的体积,则余下部分对地面的压力F甲、F乙关系是 ( )
A.F甲一定小于F乙
B.F甲可能等于F乙
C.F甲一定大于F乙
D.F甲可能大于F乙
类型二:切割+叠放问题
例4、如图所示,甲、乙为两个实心均匀正方体,它们对水平地面的压强相等。若在两个正方体的上部,沿水平方向分别截去相同高度的部分,并将截去部分叠放在对方剩余部分上.它们对地面的压强为P甲′、P乙′,下列判断正确的是 ( )
A.P甲′可能小于P乙′ B.P甲′一定大于P乙′
C.P甲′可能大于P乙′ D.P甲′一定小于P乙′
例4图
甲
乙
【答案】D.
【解析】方法一:基本公式推导
①因为它们均为实心正方体,且对地面的压强相等,设它们的边长分别为a、b,
根据p=ρ gh可得 ρ甲ga=ρ乙gb 即ρ甲a=ρ乙b
②设切去的质量分别为△ m甲、△m乙,切去的厚度为△h(如图3所示),
则△ m甲:△ m乙=ρ甲△V甲:ρ乙△V乙=ρ甲aa△h :ρ乙bb△h = a/b>1
即△ m甲>△ m乙。
③将切去部分放置在对方剩余部分的上表面时(图4),则此时
对于甲:增加的压力为△m乙g小于切去的压力△m甲g,对于水平地面的压力F甲与原来比变小,因为底面积S甲不变,根据p甲=F甲/S甲所以甲的压强与原来的比要变小。
同理叠放后乙的压强与原来的比变大。 故选D。
方法二:物理公式推导
①由于它们均为实心正方体,且对地面的压强相等,设它们的边长分别为a、b,切去的厚度为h。
根据p=ρ gh可得 ρ甲ga =ρ乙gb ρ甲a =ρ乙b ①
甲切去部分的重力 G甲切 =ρ甲gV甲切 =ρ甲ga2h ②
乙切去部分的重力 G乙切 =ρ乙gV乙切 =ρ乙gb2h ③
由①、②、③可得 G甲切 :G乙切 =ρ甲ga2h :ρ乙gb2h =a/b>1
即 G甲切>G乙切
③将切去部分放置在对方剩余部分的上表面时,则此时
对于甲:增加的压力为G乙切小于切去的压力G甲切,
所以甲对地面的压力与切去前比较 F甲<F甲前,因为底面积不变,所以压强p甲=F甲/S甲变小。
同理乙的整体产生的压强p乙=F乙/S乙变大。
故选D。
方法三:利用转化法比较切去部分的压力大小。
如图5所示,设切去的部分分别为△甲、△乙,然后转动90。后立在水平地面上,此时他们对水平面的压强相等(因为还是原来的高度),由于△S甲>△S乙,所以对水平面的压力F=PS为DF甲>DF乙。
叠放后如图6所示,再运用方法一(或二)即可比较甲与乙对水平面压强的大小关系。
类型三:旋转问题
例5、(2019年上海中考题)如图所示,均匀长方体甲、乙放在水平地面上,甲、乙的底面积分别为S、S'(S > S'),此时它们对地面的压强相等。现将甲、乙顺时针旋转90°后,甲、乙的底面积分别为S'、 S,关于此时甲、乙对地面的压强P甲、P乙和对地面的压强变化量△p甲、△P乙的大小关系,下列判断正确的是 ( )
A.P甲<p乙, △ P甲>△p乙 B.P甲<p乙, △ P甲<△p乙
C.P甲>p乙, △ P甲>△p乙 D . P甲>p乙, △ P甲<△p乙
例5图
甲
乙
【答案】B.
【解析】①由题意可知现将甲、乙顺时针旋转90°后,甲的受力面积变大,故对地压强变小。乙的受力面积变小,对地压强变大。而原来二者的对地压强相等,所以可得p甲
原来P甲=P乙 即ρ甲gh甲=ρ乙gh乙 因为 h甲>h乙 所以甲、乙密度的大小关系为ρ甲<ρ乙。③翻转之后甲、乙对地面的压强变化量分别为:△P甲=ρ甲g△h甲,△P乙=ρ乙g△h乙,
因为△h甲=△h乙,ρ甲<ρ乙,所以 △P甲<△P乙 。
类型四:竖直切割问题
例6、甲、乙两个实心正方体分别放在水平地面上,已知甲和乙两个物体的质量相等,密度关系为ρ甲>ρ乙,若把它们都沿竖直方向切去质量相等的部分,则两个正方体剩下部分对水平地面的压强大小关系 ( )
A. p甲=p乙 B. p甲<p乙
C. p甲>p乙 D. 以上都有可能
【答案】C.
【解析】①甲和乙两个物体的质量相等,m甲=m乙,即ρ甲V水=ρ乙V乙,因为ρ甲>ρ乙,所以甲、乙的体积关系为 V甲<V乙,其大小关系如图6所示。
②如图6 所示,底面积的大小关系为S甲<S乙,m甲=m乙,压力的大小关系为F甲=F乙,
根据p=F/S=G/S=mg/S,原来甲、乙压强的大小关系为p甲>p乙。
③若把它们都沿竖直方向切去质量相等的部分,则两个正方体剩下部分对水平地面的压强都不变,还是p甲>p乙。
所以选C。
培优· 训练
1、水平桌面上有一个质量为m的长方体木块,木块与桌面的接触面积为S,则木块对桌面的压强p1=________。如图所示,将木块沿竖直方向切掉一部分,则剩余部分对桌面的压强p2________p1(选填“>”、“=”或“<”)。
第1题图 第2题图
2、(多选)如图所示,质量分布均匀的物体A、B放在水平地面上,高度相同,A的底面积大于B的底面积,A对地面的压力小于B对地面的压力。若在两物体上部沿水平方向切去相同的厚度,mA′、mB′分别表示A、B剩余部分的质量,pA′、pB′分别表示剩余部分对地面的压强.下列判断正确的是( )
A.mA′>mB′ B.mA′
A.p甲
B
第3题图 第4题图 第5题图
4、如图所示,一个质量均匀的木块放在水平地面上,现在沿虚线方向将木块锯成A和B两部分,它们对地面的压强分别为pA和pB,则( )
A .pA<pB B .pA=pB C .pA>pB D .无法比较
5、将一均匀长方体放在水平桌面上,如图1所示.若沿虚线切开拿走左上方的一半, 则长方体的密度、长方体对桌面的压力及压强的变化是( )
A.密度不变,压强不变,压力减小 B.密度减小,压强减小,压力减小
C.密度不变,压强不变,压力不变 D.密度不变,压强减小,压力减小
6、如图所示,水平面上放置了质地均匀的甲、乙两个实心圆柱体,它们的高度相同,质量相等,甲的底面积小于乙的底面积,为使甲对水平面的压强小于乙对水平面的压强,小海按不同方法把甲、乙两物体分别切下一部分后,将切下的部分叠加到对方剩余部分的上方,下列切法可能达到目的的是 ( )
A.沿水平方向切去质量相等的部分 B.沿水平方向切去体积相等的部分
C.沿水平方向切去厚度相等的部分 D.沿竖直方向切去质量相等的部分
甲
乙
第6题图
7、如图所示,甲、乙两个用同种材料制成的均匀实心正方体放在水平地面上,可能使甲和乙对地面的压强相等的方法是 ( )
甲
乙
第7题图
A、沿水平线截去质量相同的部分。
B、沿水平线截去高度相同的部分。
C、将质量相同的物体分别放在甲、乙的上面。
D、分别以甲、乙物体上表面的面积大小加上相同高度的该种物质。
8、如图所示,质量相同的甲、乙两个均匀实心正方体放在水平地面上。若分别沿竖直方向截去厚度相等的部分后,则剩余部分对水平地面的压强p甲和p乙的关系为( )
A、p甲<p乙 B、p甲=p乙 C、p甲>p乙 D、不确定
甲
乙
第8题图
9、如图所示,A、B两实心立方体分别放在水平地面上,它们对水平地面的压强相等,现将两立方体沿竖直方向各切去相同的宽度,再将切去的部分放在各自的上表面,则此时它们对水平地面的压强大小关系为( )
A、pA>pB B、pA<pB C、pA=pB D、无法判断。
A
B
A
A
10、甲、乙两个均匀实心正方体分别放在水平地面上,它们对地面的压强相等,已知甲的密度<乙的密度.沿竖直方向分别截去相同的质量,则剩余部分对水平地面的压强关系是:_____________.
11、甲、乙两个实心立方体分别放在水平地面上(ρ甲<ρ乙),它们对水平地面的压强相等。若沿竖直方向将甲、乙两个立方体各切除质量相同的一部分,再将切除部分分别叠放在各自剩余部分上面,则水平地面受到甲、乙的压强( )
A.p甲<p乙 B.p甲=p乙 C.p甲>p乙 D.以上情况均有可能
12、如图所示,甲、乙、丙三个实心立方体分别放在水平地面上,它们对水平地面的压强关系大小关系是p甲>p乙>p丙相等,现在三个正方体的水平方向截去相同的高度,则剩余部分对水平地面的压强大小关系为( )
A、 p甲>p乙>p丙 B、 p甲=p乙=p丙 C、 p甲
乙
甲
第12题图
13、如图所示,两个实心圆柱体放置在水平地面上。沿水平方向截去其上部相同高度后,剩余部分对水平地面的压强相等。则它们原来对水平地面的压强关系是 ( )
A、p甲 = p乙 B、 p甲 < p乙 C、p甲 > p乙 D、无法判断
甲
乙
第13题图 甲
乙
第14题图
14、如图14所示,甲、乙两个实心均匀正方体分别放在水平桌面上,他们对桌面的压强相等, 甲、乙两个正方体的边长之比为6:5,若在两个正方体的上部沿水平方向都截去甲边长的1/3,则甲、乙两个正方体剩余部分对水平地面的压强之比为( )
A.6:5 B.5:6 C.10:9 D.9:10
15、如图所示,甲、乙两个实心正方体分别放在水平地面上,它们对地面的压强相等,若沿水平方向截去相同的体积,则剩余部分对水平地面的压强关系是( )
A、 p甲 < p乙 B、p甲 = p乙 C、p甲 > p乙 D、无法判断
16、甲、乙、丙三个实心正方体分别放在水平地面上,它们对水平地面的压强相等,它们的密度ρ甲<ρ乙<ρ丙 。若在两正方体上方截去质量相同的部分,则剩余部分对水平地面的压强关系为( )
A、P甲
A.△m甲=△m乙=△m丙。 B. △m甲>△m乙>△m丙。
C. △m甲<△m乙<△m丙。 D. △m甲>△m丙>△m乙。
18、甲、乙、丙三个实心立方体分别放在水平地面上,它们对水平地面的压强相等,已知ρ甲<ρ乙<ρ丙,若在甲、乙、丙三个立方体上分别放一个质量相等的铜块,则三个立方体对水平地面的压强大小关系为 ( )
、
A.P甲
19、如图甲所示,钢制的圆柱展示台,底面积S=1 dm2,另一个为钢制的圆台零件,上底面积S1=3 dm2,下底面积S2=12 dm2。把零件分别按图乙和图丙所示的方式静置在展示台上,两物体的轴在同一直线上。图乙中零件对展示台面的压力为F1,压强为p1。图丙中零件对展示台面的压力为F2,压强为p2。则F1_______F2. p1 p2。(均选填“>”“=”或“<”)
20、如图所示,将圆柱体甲、乙放在水平面上,已知ρ甲>ρ乙.若沿水平方向切除相同的高度Δh,则下列图像中能正确表示余下部分对地面的压强p′与切去部分的高度Δh的关系是( )
21、(2020虹口一模)如图所示,形状、体积相同的长方体甲、乙置于水平地面,对地面的压力分别为F甲、F乙,将它们顺时针旋转90°,此时甲、乙对地面的压强分别为 p甲′、p乙′,对地面压强的变化量分别为Δp甲、Δp乙。若Δp甲>Δp乙,则( )
图
乙
甲
甲
乙
A.F甲>F乙,p甲′>p乙′ B.F甲>F乙,p甲′<p乙′
C.F甲<F乙,p甲′>p乙′ D.F甲<F乙,p甲′<p乙′
微专题9-3 切割体的压强
例1、【答案】
【解析】本题考察固体压强的切割问题。此类问题通常有两种解题思路:
思路一:根据,分别考虑压力和受力面积的变化,据此分析压强的变化。
思路二:根据柱形固体压强计算式,分析高度是否变化。
首先看横向切割,如图1所示:
方法一:根据,横向切割后,压力变小,受力面积不变,故压强变小。
方法二:木块横切后仍是柱体,利用计算式分析,剩余木块的密度不变,高度变小,故压强变小。
再看竖直切割,如图2所示:
方法一:采用特殊值法,假设切去整体的三分之一
则剩余部分对桌面的压强 即竖切前后压强不变。
方法二:木块竖直切割后仍是柱体,利用计算式分析,剩余木块的密度和高度均不变,故压强不变。
比较两种方法,发现通过计算式来分析横切或竖切问题都较为简便。
最后看下不规则切割,如图3所示。切割后,左右两部分对桌面的压力均变小,同时与桌面的接触面积也均变小,压强如何变化呢?对于这种不规则切割,可利用割补法转化为柱体进行分析。
图4
如图4所示将左半部分分为I、Ⅱ两部分,可以理解为在木块I上叠加了木块Ⅱ。木块I是柱体,和原木块相比,高度不变,密度不变,由计算式知木块I对桌面的压强不变。在木块I上叠加了木块Ⅱ,与桌面接触面积S3不变,但对桌面压力变大(),则压强变大,即p3>p0。
将右半部分按图5中虚线所示补成新柱体。该柱体和切割前的木块相比,高度不变,密度不变,由计算式知该柱体对桌面的压强等于p0。该柱体切掉部分Ⅱ后,压力变小(),受力面积S4不变,故压强变小,即p4
例2、【答案】B.
【解析】本题考查切割柱体的压强问题。涉及到压强的变化量,通常采用变化量法求解:
(1)当受力面积不变时
(2)柱状物体压强问题中,当密度不变时
下面来分析本题:
未截前p甲=p乙,分别沿水平方向截去一部分后,p′甲>p′乙
所以△p甲<△p乙
由得:
即
故B正确,A错误。
再来看下选项C。截去相同的体积,质量大小关系呢?要先判断下密度关系。
由得:
图中
则
即截去相同体积,不符合我们之前的判断,C错误。
再来看D选项。一定是截去相同高度吗?分析一下:
由得:
由于
则,即一定是甲截去的高度小于乙截去的高度。D错误。
回顾整道题,主要是利用变化量法求解,注意推导过程一定要严谨!
有没有更快速的做题方法呢?有!极限法!
看下选项A,提到截去相同的质量,不妨将其中最轻的一个全部截去。我们从p甲=p乙,S甲
同样的方法也可以用于判断BCD选项。同学们自己思考下。
例3、【答案】C.
【解析】方法一:基本公式推导
第一步先比较甲与乙密度的大小关系:
第二步比较变化的压强△P的大小关系,运用沿水平方向分别截去相同的高度,
第三步用P'=P原来-△P比较切割后压强的大小,
第四步根据P=F/S判断质量的大小,
方法二:图像法
对于所有均匀柱体水平切割问题,我们都可以把它转化为函数图像来解决。
根据
P与m成正比,m与h成正比,那么p也与h成正比,
令:原压强为p,原高度为h,水平切割后新压强为p',切割的高度为△h,则新高度为h-△h,
故有: →
可以看出p'与△h为一次函数,
作出甲乙的p'与△h一次函数, (由题干中的图可知:h1>h2)
由图像可以轻易看出p1>p2
同理,也可以做出p'与△m 的函数图像,就可以轻易得出结论
推而广之,关于均匀柱体水平横切等等问题,诸如:F与体积、质量、高度;p与体积、质量、高度都可以转化为图像来解决。
当然有很多同学认为,函数图像很难想到,写出函数关系,作出图像本身有难度,此类问题何必如此复杂,直接用极限法或者特殊值法不是更简单明了吗?
在这里我要说明两点:
①极限法或者特殊值法虽然简单,但是理解不透彻或者考虑不全面就极易犯错;
②图像法是一种重要的思想方法,以后高中会成为基本方法,对于数学较好的同学而言,此法更易理解,熟练之后一样快捷。对于以后的物理以及数学学习会很有帮助!
易错题链接
1、C 2、B、
例4、【答案】D.
【解析】方法一:基本公式推导
①因为它们均为实心正方体,且对地面的压强相等,设它们的边长分别为a、b,
根据p=ρ gh可得 ρ甲ga=ρ乙gb 即ρ甲a=ρ乙b
②设切去的质量分别为△ m甲、△m乙,切去的厚度为△h(如图3所示),
则△ m甲:△ m乙=ρ甲△V甲:ρ乙△V乙=ρ甲aa△h :ρ乙bb△h = a/b>1
即△ m甲>△ m乙。
③将切去部分放置在对方剩余部分的上表面时(图4),则此时
对于甲:增加的压力为△m乙g小于切去的压力△m甲g,对于水平地面的压力F甲与原来比变小,因为底面积S甲不变,根据p甲=F甲/S甲所以甲的压强与原来的比要变小。
同理叠放后乙的压强与原来的比变大。 故选D。
方法二:物理公式推导
①由于它们均为实心正方体,且对地面的压强相等,设它们的边长分别为a、b,切去的厚度为h。
根据p=ρ gh可得 ρ甲ga =ρ乙gb ρ甲a =ρ乙b ①
甲切去部分的重力 G甲切 =ρ甲gV甲切 =ρ甲ga2h ②
乙切去部分的重力 G乙切 =ρ乙gV乙切 =ρ乙gb2h ③
由①、②、③可得 G甲切 :G乙切 =ρ甲ga2h :ρ乙gb2h =a/b>1
即 G甲切>G乙切
③将切去部分放置在对方剩余部分的上表面时,则此时
对于甲:增加的压力为G乙切小于切去的压力G甲切,
所以甲对地面的压力与切去前比较 F甲<F甲前,因为底面积不变,所以压强p甲=F甲/S甲变小。
同理乙的整体产生的压强p乙=F乙/S乙变大。
故选D。
方法三:利用转化法比较切去部分的压力大小。
如图5所示,设切去的部分分别为△甲、△乙,然后转动90。后立在水平地面上,此时他们对水平面的压强相等(因为还是原来的高度),由于△S甲>△S乙,所以对水平面的压力F=PS为DF甲>DF乙。
叠放后如图6所示,再运用方法一(或二)即可比较甲与乙对水平面压强的大小关系。
例5、【答案】B.
【解析】①由题意可知现将甲、乙顺时针旋转90°后,甲的受力面积变大,故对地压强变小。乙的受力面积变小,对地压强变大。而原来二者的对地压强相等,所以可得p甲
原来P甲=P乙 即ρ甲gh甲=ρ乙gh乙 因为 h甲>h乙 所以甲、乙密度的大小关系为ρ甲<ρ乙。③翻转之后甲、乙对地面的压强变化量分别为:△P甲=ρ甲g△h甲,△P乙=ρ乙g△h乙,
因为△h甲=△h乙,ρ甲<ρ乙,所以 △P甲<△P乙 。
例6、【答案】C.
【解析】①甲和乙两个物体的质量相等,m甲=m乙,即ρ甲V水=ρ乙V乙,因为ρ甲>ρ乙,所以甲、乙的体积关系为 V甲<V乙,其大小关系如图6所示。
②如图6 所示,底面积的大小关系为S甲<S乙,m甲=m乙,压力的大小关系为F甲=F乙,
根据p=F/S=G/S=mg/S,原来甲、乙压强的大小关系为p甲>p乙。
③若把它们都沿竖直方向切去质量相等的部分,则两个正方体剩下部分对水平地面的压强都不变,还是p甲>p乙。
所以选C。
专题提升训练
1、=
2、BD
3、B
4、C
5、D
6、B
[解析]由题可知,m甲=m乙,S甲
7、C
8、B
9、B
10、相等
11、A
12、D
13、C
14、C
15、C
16、C
17、B
18、A
19、= =
[解析]零件对展示台面的压力等于零件自身的重力,所以F1=F2;乙、丙两图中展示台面所受压力的受力面积相等,根据p=可知,p1=p2。
20、D
【解析】由于甲和乙是规则圆柱体,由固体压强公式p======ρgh可知,圆柱体对地面的压强与其高度成正比,当甲和乙沿水平方向切除相同的高度Δh后,截取高度Δh越大,甲乙圆柱体对地面的压强越小,A错误;由于ρ甲>ρ乙,且甲剩余的高度高,因此剩余部分甲对地面的压强总是大于乙对地面的压强,B错误;又由p=ρgh,ρ甲>ρ乙可得,截去相同Δh后,甲的变化量大于乙的变化量,甲曲线下降的快,C错误,D正确.故选D.
21、【答案】A
2022年通用物理中考微专题-浮力-10-5 液面变化与压强(含答案): 这是一份2022年通用物理中考微专题-浮力-10-5 液面变化与压强(含答案),共7页。学案主要包含了常用公式,基本步骤等内容,欢迎下载使用。
2022年通用物理中考微专题-压强-9-7 压强相关实验(含答案): 这是一份2022年通用物理中考微专题-压强-9-7 压强相关实验(含答案),共9页。学案主要包含了设计和进行实验,实验结论,数据处理和分析等内容,欢迎下载使用。
2022年通用物理中考微专题-压强-9-6 气体压强问题(含答案): 这是一份2022年通用物理中考微专题-压强-9-6 气体压强问题(含答案),共9页。













