

吉林省四平市铁东区2021-2022学年八年级下学期期末数学试题(word版含答案)
展开这是一份吉林省四平市铁东区2021-2022学年八年级下学期期末数学试题(word版含答案),共13页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
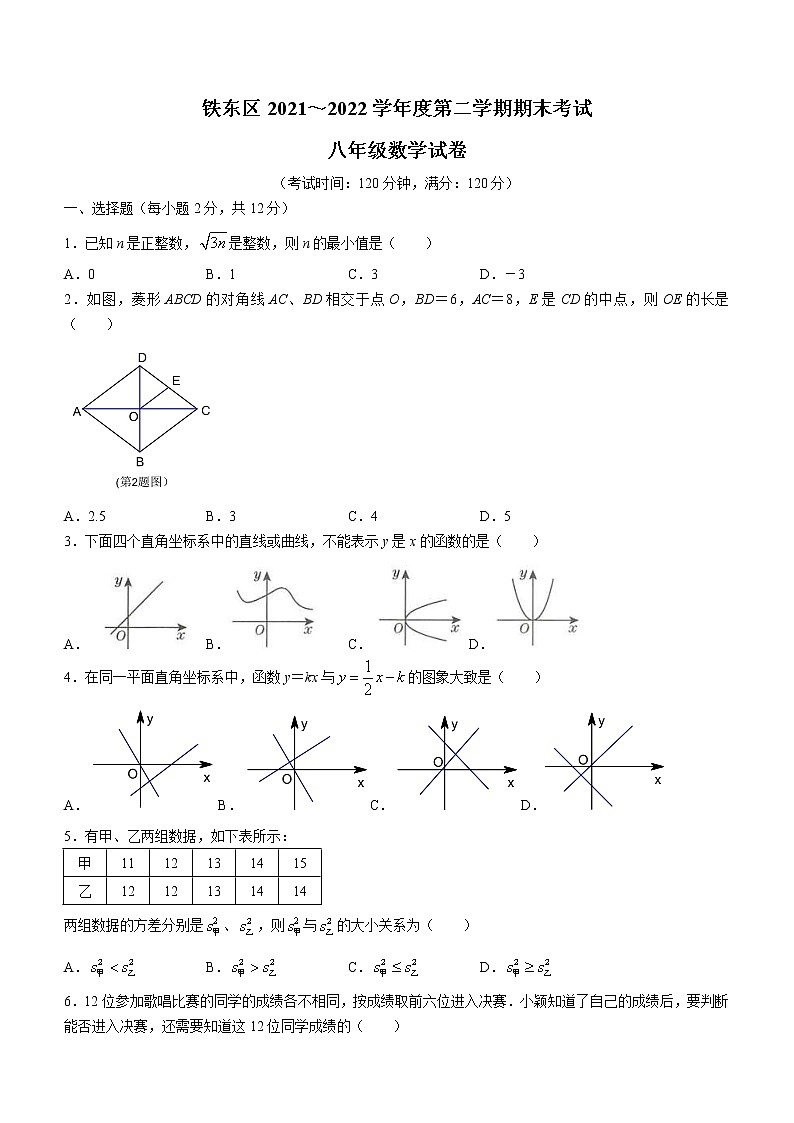
铁东区2021~2022学年度第二学期期末考试
八年级数学试卷
(考试时间:120分钟,满分:120分)
一、选择题(每小题2分,共12分)
1.已知n是正整数,是整数,则n的最小值是( )
A.0 B.1 C.3 D.-3
2.如图,菱形ABCD的对角线AC、BD相交于点O,BD=6,AC=8,E是CD的中点,则OE的长是( )
A.2.5 B.3 C.4 D.5
3.下面四个直角坐标系中的直线或曲线,不能表示y是x的函数的是( )
A. B. C.D.
4.在同一平面直角坐标系中,函数y=kx与的图象大致是( )
A.B.C.D.
5.有甲、乙两组数据,如下表所示:
甲 | 11 | 12 | 13 | 14 | 15 |
乙 | 12 | 12 | 13 | 14 | 14 |
两组数据的方差分别是、,则与的大小关系为( )
A. B. C. D.
6.12位参加歌唱比赛的同学的成绩各不相同,按成绩取前六位进入决赛.小颖知道了自己的成绩后,要判断能否进入决赛,还需要知道这12位同学成绩的( )
A.方差 B.平均数 C.众数 D.中位数
二、填空题(每小题3分,共24分)
7.若在实数范围内有意义,则x的取值范围是______.
8.如图,在△ABC中,D、E、F分别是AB、BC、CA的中点.若△ABC的面积为3,则的面积为______.
9.一个木匠要制作矩形的踏板.他在一个对边平行的长木板上分别沿与长边垂直的方向锯两次,就能得到矩形踏板.理由是______.
10.如图,甲、乙两艘客轮同时离开港口,航行的速度都是40m/min,甲客轮用15min到达点A,乙客轮用20min到达点B.若A,B两点的直线距离为1000m,甲客轮沿着北偏东30°的方向航行,则乙客轮的航行方向是______.
11.函数的图象如图所示,则这个函数的最小值是______.
12.在校园歌手大奖赛上,比赛规则是:七位评委打分,去掉一个最高分和一个最低分后,所剩数据取平均数即为选手的最后得分.七位评委给某位歌手打出的分数如下:9.5,9.4,9.6,9.9,9.3,9.7,9.0,则这位歌手的最后得分是_____.
13.若函数y=2x+3与y=3x-2b的图象交x轴于同一点,则b的值为______.
14.如图,已知直线和直线的交点坐标是(m,n),则关于x的不等式的解集是______.
三、解答题(每小题5分,共20分)
15.计算:
16.如图,在中,点E,F分别在BC、AD上,且DF=BE.
求证:四边形AECF是平行四边形.
17.(1)在直角坐标系中画出直线;
(2)将直线向上平移1个单位得到直线,请直接写出直线的函数解析式为_______________.
18.如图,四边形ABCO是平行四边形,A、B两点的坐标分别为(6,0),(2,4).
(1)点C的坐标为______;
(2)求直线OC的函数解析式.
四、解答题(每小题7分,共28分)
19.如图,的对角线相较于点O,△OAB是等边三角形,AB=4.
(1)求证:是矩形;
(2)求AD的长.
20.如图,在△ABC中,∠BAC=90°,AD是BC边上的中线,点E是AD的中点,过点A作,交BE的延长线于点F,连接CF.
(1)求证:四边形ADCF是菱形;
(2)若AB=AC,试判定四边形ADCF的形状.
21.如图,已知过点B(1,0)的直线与直线相交于点P(-1,a).
(1)求直线的函数解析式;
(2)设直线与y轴交点为C,求四边形PAOC的面积.
22.某实验中学八年级甲、乙两班分别选5名同学参加“学雷锋读书活动”演讲比赛,其预赛成绩如图所示:
(1)根据上图填写下表:
| 平均数 | 众数 | 中位数 | 方差 |
甲班 | 8.5 | 8.5 |
| 0.7 |
乙班 | 8.5 |
| 8 | 1.6 |
(2)请你分别从平均数、众数、中位数和方差四个方面评价甲、乙两班的预赛成绩,并说明你的理由;
(3)乙班小明说:“我的成绩是中等水平”,你知道他是几号选手?
五、解答题(每小题8分,共16分)
23.甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶.已知甲先出发6分钟后,乙再出发,在整个过程中,甲、乙两人的距离y(千米)与甲出发的时间x(分)之间的关系如图所示.
(1)A、B两地的距离是______千米,乙的速度是______千米/分;
(2)乙到达终点后,甲还需______分钟到达终点B地;
(3)求整个过程中y与x的函数解析式,并指出自变量x的取值范围.
24.某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如下表:
| 原进价(元/张) | 零售价(元/张) | 成套售价(元/套) |
餐桌 | a | 270 | 500 |
餐椅 | a-110 | 70 |
已知用600元购进的餐桌数量与用160元购进的餐椅数量相同.
(1)上表中a的值为______;
(2)若该商场购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.该商场计划将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,其余餐桌、餐椅以零售方式销售.请问怎样进货,才能获得最大利润?最大利润是多少?
六、解答题(每小题10分,共20)
25.如图,在平面直角坐标系中,直线y=-x+8分别交两坐标轴于点A、B,直线CD与直线AB交于点C,与x轴交于点D.点C的横坐标为4,点D在线段OA上,且AD=7.
(1)C、D两点的坐标分别为______;
(2)求直线CD的函数解析式;
(3)在坐标平面内是否存在这样的点F,使以A、C、D、F为顶点的四边形为平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由.
26.如图,在矩形ABCD中,AB=4,AD=3,连结BD.点P从点A出发,沿折线AB-BD-DC以每秒1个单位长度的速度向终点C运动.以AP为对角线作正方形AEPF(点F在直线AP的右侧).设正方形AEPF的面积为S(平方单位),点P的运动时间为t(秒).
(1)当点P在线段AB上时,求出S与t之间的函数关系式,并写出t的取值范围;
(2)当点P在线段DC上时,求出S与t之间的函数关系式,并写出t的取值范围;
(3)当直线BF将正方形AEPF分成的两部分图形面积相等时,求出t的值.
铁东区2021~2022学年度第二学期期末考试
八年级数学试题参考答案
一、选择题(每小题2分,共12分)
1.C 2.A 3.C 4.B 5.B 6.D
二、填空题(每小题3分,共24分)
7.x≥0 8.(或者:0.75) 9.四个角都是直角的四边形是矩形(或者:“有一个角是直角的平行四边形是矩形”) 10.北偏西60° 11.1 12.9.5 13. 14.x<m
三、解答题(每小题5分,共20分)
15.原式
16.证明:∵四边形ABCD是平行四边形,∴,AD=BC.
又∵DF=BE,∴AF=EC.
∵,AF=EC,∴四边形AECF是平行四边形.
17.(1)图象画正确;
(2)y=x
18.(1)(-4,4)
(2)设直线OC的函数解析式为y=kx
将点C的坐标(-4,4)代入之,得k=-1,∴y=-x.
19.(1)证明:∵四边形ABCD是平行四边形,∴AO=OC,BO=OD.
∵△OAB是等边三角形,∴AO=BO=AB,
∴AC=BD,∴是矩形.
(2)∵四边形ABCD是矩形,∴∠BAD=90°.
又∵BO=AB=4,∴BD=8.
在中,,.
20.(1)证明:∵点E是AD的中点,∴AE=DE.
∵,∴∠DAF=∠3.又∵∠1=∠2,∴.
(方法一)
∴AF=BD.∵AD是斜边BC边上的中线,:∴AD=BD=DC.∴AF=DC.
又∵,∴四边形ADCF是平行四边形.
(方法二)
∴BE=FE,点E是AD的中点.
∵AD是BC边上的中线,∴点D是BC的中点
∴DE是的中位线,∴.
又∵,∴四边形ADCF是平行四边形
(注意:证明方法的灵活多样)
∵∠BAC=90°,AD是斜边BC边上的中线,∴AD=DC,
∴四边形ADCF是菱形.
(2)∵四边形ADCF是菱形,∴∠4=∠5.
当AB=AC时,∠4=∠ABC=45°,∴∠DCF=90°,
∴四边形ADCF是正方形.
21.(1)将P(-1,a)代入y=2x+4,得a=2,∴P(-1,2)
设直线的函数解析式为y=kx+b,
将P(-1,2)、B(1,0)分别代入y=kx+b,
得,解得,∴y=-x+1.
(2)将x=0代入y=-x+1,得y=1.∴C(0,1),0C=1.
将y=0代入y=2x+4,得x=2∴A(-2,0),0A=2.
.
22.
| 平均数 | 众数 | 中位数 | 方差 |
甲班 | 8.5 | 8.5 | 8.5 | 0.7 |
乙班 | 8.5 | 10 | 8 | 1.6 |
(1)每空1分
(2)从平均数看,因为甲班和乙班成绩的平均数相同,所以成绩一样好;
从众数看,因为乙班的高于甲班的,所以乙班的成绩比较好;
从中位数看,甲班的高于乙班的,所以甲班的成绩比较好;
从方差看,甲班的方差小,甲班的成绩波动小,更稳定,所以甲班的成绩比较好.
(3)乙班小明是5号选手.
23.(1)A、B两地的距离是16千米,
乙的速度是千米/分;
(2)乙到达终点后,甲还需_78分钟到达终点B地;
(3)当0≤x≤6时,;
当6<x≤16时,;
当16<x≤18时,;
当18<x≤96时,.
综上所述,y与x的函数解析式为
说明:第(3)问,每个分段函数的解析式和自变量的取值范围正确得1分,共4分.
24.(1)求表中a的值为150;
(2)解:∵a=150,∴a-110=40.
设购进餐桌x张,餐椅(5x+20)张,获得利润为y,
则
=245x+600
∵245>0,∴y随x的增大而增大.
∵x+(5x+20)≤200,∴x≤30.
∴当x=30时,y有最大值.
,
此时,2x+50=110
答:购进餐桌30张,餐椅110张时,获得利润最大,最大利润是7950元.
25.(1)C(4,4),D(1,0);
(2)解:设直线CD的函数解析式为y=kx+b,
将C(4,4)、D(1,0)代入之,得
解得,.∴.
(3)存在.
当AC是对角线时,点F在AC的右侧,,CF=DA.;
当DC是对角线时,点F在DC的左侧,,CF=DA.F(-3,4);
当DA是对角线时,点F在DA的下方,
,AF=CD;,DF=CA.
作FG⊥x轴于点G,CH⊥x轴于点H,可证明
,FG=CH,AG=DH.∴F(5,-4).
∴点F的坐标为(11,4),或者(-3,4),或者(5,-4).
(温馨提示:该题解法不唯一,也可先求出AF和DF的函数解析式,再求它们的交点坐标)
26.解:∵AB=4,AD=3,∴BD=5.
设正方形边长为x,则,.
(1)当点P在线段AB上时,∵AP=t,
∴.
(2)当点P在线段DC上时,AD=3,DP=t-9,
.
(3)解:当点P在线段AB上时,直线BF不可能将正方形AEPF分成面积相等的两部分;
当点P在线段BD上,且PB=AB时,BF垂直平分AP,
直线BF将正方形AEPF分成的两部分图形面积相等.
此时,PB=AB=4,t=4+4=8;.
当点P在线段DC上,且PB=AB时,BF垂直平分AP,直线BF将正方形AEPF分成
的两部分图形面积相等.此时,,.
又∵PC=4+5+4-t=13-t,13-t≥0,∴,.
∴当直线BF将正方形AEPF分成的两部分图形面积相等时,t的值为8或者.
相关试卷
这是一份吉林省四平市铁东区2022-2023学年八年级下学期期末数学试题(原卷版+解析版),文件包含精品解析吉林省四平市铁东区2022-2023学年八年级下学期期末数学试题原卷版docx、精品解析吉林省四平市铁东区2022-2023学年八年级下学期期末数学试题解析版docx等2份试卷配套教学资源,其中试卷共33页, 欢迎下载使用。
这是一份2022-2023学年吉林省四平市铁东区八年级下学期期末数学试卷(文字版含答案解析),共23页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份吉林省四平市铁东区2022-2023学年八年级下学期7月期末数学试题,共8页。












