【通用版】2023届高考数学一轮复习计数原理与概率统计专练（9）二项分布及其应用

这是一份【通用版】2023届高考数学一轮复习计数原理与概率统计专练（9）二项分布及其应用，共7页。试卷主要包含了设随机变量，则等于，7B等内容，欢迎下载使用。
（9）二项分布及其应用1.甲、乙两人参加“社会主义价值观”知识竞赛，甲、乙两人能荣获一等奖的概率分别为和，甲、乙两人是否获得一等奖相互独立，则这两个人中恰有一人获得一等奖的概率为(   )A. B. C. D.2.从混有5张假钞的20张百元钞票中依次抽出2张，将第1张放到验钞机上检验发现是假钞，则第2张也是假钞的概率为(   )
A. B. C. D.3.袋中装有标号为1，2，3，4，5，6且大小相同的6个小球，从袋中一次性摸出两个球，记下号码并放回，若两个号码的和是3的倍数，则获奖.现有5人参与摸球，则恰好2人获奖的概率是(   )
A. B. C. D.4.设随机变量，则等于(   )
A. B. C. D.5.电路从A到B上共连接着6个灯泡(如图)，每个灯泡断路的概率是，整个电路的连通与否取决于灯泡是否断路，则从A到B连通的概率是(   )A. B. C. D.6.某单位派出甲、乙等5名志愿者进入富强等4个社区宣讲十九届六中全会精神，每名志愿者只去1个社区，每个社区至少有1名志愿者，则在甲去富强社区宣讲的条件下，乙不去富强社区宣讲的概率为(   )A. B. C. D.7.某群体中的每位成员使用移动支付的概率都为p，各成员的支付方式相互独立.设X为该群体的10位成员中使用移动支付的人数，，则(   )A.0.7 B.0.6 C.0.4 D.0.38.某市环保局举办“六·五”世界环境日宣传活动，进行现场抽奖.抽奖规则:盒中装有10张大小相同的精美卡片，卡片上分别印有“环保会徽”或“绿色环保标志”图案.参加者每次从盒中抽取两张卡片，若抽到两张都是“绿色环保标志”卡即可获奖.已知从盒中抽取两张都不是“绿色环保标志”卡的概率是.现有甲、乙、丙、丁四人依次抽奖，抽后放回，另一人再抽，用X表示获奖的人数，那么(   )
A. B. C. D.9.已知1号箱中有2个白球和4个红球，2号箱中有5个白球和3个红球（白球与红球大小、形状、质地相同），现随机从1号箱中取出一球放入2号箱，再从2号箱中随机取出一球，则两次都取到红球的概率是(   )
A. B. C. D.10.现有10张分别标有-5，-4，-3，-2，-1，0，1，2，3，4的卡片，它们的大小和颜色完全相同，从中随机抽取1张，记下数后放回，连续抽取3次，则记下的数中有正有负且没有0的概率为(   )
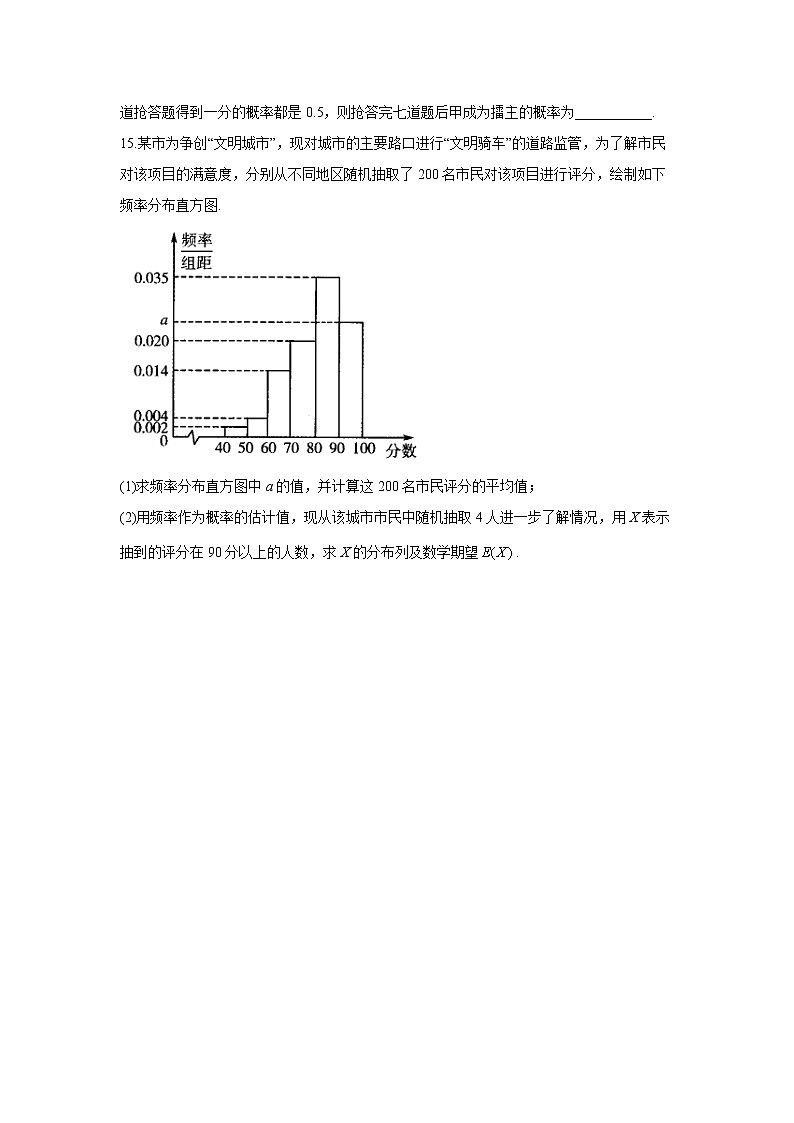
A. B. C. D.11.某班有6名班干部，其中男生4人，女生2人.从中任选3名班干部参加学校的义务劳动.设“男生甲被选中”为事件A，“女生乙被选中”为事件B，则_____________.12.设某批电子手表的正品率为，次品率为，现对该批电子手表进行检测，每次抽取一个电子手表，假设每次检测相互独立，则第3次首次检测到次品的概率为___________.13.设随机变量，则_______.14.《中国诗词大会》是央视首档全民参与的诗词节日，节目以“赏中华诗词，寻文化基因，品生活之美”为宗旨每一期的比赛包含以下环节：“个人追逐赛”“攻擂资格争夺赛”和“擂主争霸赛”，其中“擂主争霸赛”由“攻擂资格争夺赛”获胜者与上一场擂主进行比拼.“擂主争霸赛”共有九道抢答题，抢到并答对者得一分，答错则对方得一分，率先获得五分者即为该场擂主.在《中国诗词大会》的某一期节目中，若进行“擂主争霸赛”的甲、乙两位选手每道抢答题得到一分的概率都是0.5，则抢答完七道题后甲成为擂主的概率为___________.15.某市为争创“文明城市”，现对城市的主要路口进行“文明骑车”的道路监管，为了解市民对该项目的满意度，分别从不同地区随机抽取了200名市民对该项目进行评分，绘制如下频率分布直方图.(1)求频率分布直方图中a的值，并计算这200名市民评分的平均值；(2)用频率作为概率的估计值，现从该城市市民中随机抽取4人进一步了解情况，用X表示抽到的评分在90分以上的人数，求X的分布列及数学期望.
答案以及解析1.答案：D解析：根据题意，恰有一人获得一等奖就是甲获得乙没获得或甲没获得乙获得，则所求概率是，故选D2.答案：C解析：设事件A表示“抽到的第1张是假钞”，事件B表示“则抽到的第2张是假钞”，则，，所以.3.答案：C解析：从6个小球中摸出两个小球，共有种情况，
两个球的号码之和是3的倍数，共有，，，，种情况，
获奖的概率是，
因此5人参与摸球，相当于5重伯努利试验，且每次获奖的概率均为，所求概率.
故选C.4.答案：A解析：由二项分布的概率公式可得，，故选A.5.答案：B解析：由题意，可知AC之间未连通的概率是，连通的概率是.EF之间连通的概率是，未连通的概率是，故CB之间未连通的概率是，故CB之间连通的概率是，故AB之间连通的概率是，故选B.6.答案：A解析：甲去富强社区宣讲的事件记作A，甲去富强社区宣讲，乙不去富强社区宣讲的事件记作B.方法一：甲去富强社区宣讲有(种)情况，其中乙不去富强社区宣讲有(种)情况.根据古典概型的概率计算公式，得.故选A.方法二：由已知条件，得，，根据条件概率公式，得.故选A.7.答案：B解析：由题意得.因为，所以，解得或.因为，所以，即，解得，所以.故选B.8.答案：A解析：设盒中印有“环保会徽”图案的卡片有n张，则印有“绿色环保标志”图案的卡片有张，由题意得，所以，
所以参加者每次从盒中抽取两张卡片，获奖的概率，
因此，
所以.
故选A.9.答案：C解析：设“从1号箱中取到红球放入2号箱”为事件A，“从2号箱中取到红球”为事件B.由题意，知，，所以，所以两次都取到红球的概率为.故选C.10.答案：B解析：由题意，知每次抽到标有正数的卡片的概率为，抽到标有负数的卡片的概率为，抽到标有0的卡片的概率为，而记下的数中有正有负且没有0的情况有两种:2正1负，1正2负，则所求的概率为.11.答案：解析：根据题意，事件“男生甲被选中且女生乙被选中”发生的概率为，事件“男生甲被选中”发生的概率为..12.答案：解析：因为第3次首次检测到次品，所以第1次和第2次检测到的都是正品，第3次检测到的是次品，所以第3次首次检测到次品的概率为.13.答案：解析：因为随机变量，
所以
.14.答案：解析：抢答完七道题后甲成为擂主，则第7题甲得1分，前6题甲得4分，乙得2分，甲最后以获胜，其概率.15.答案：(1)；平均分为80.70分.(2)分布列见解析，数学期望为1.解析：(1)由频率分布直方图知，，由，解得，(分).(2)评分在90分以上的频率为0.25，用频率作为概率的估计值，现从该城市中随机抽取4人可以看成二项分布，X的所有可能取值为0，1，2，3，4，，，，，，所以X的分布列为：X01234P.