【通用版】2023届高考数学一轮复习计数原理与概率统计专练（11）回归分析及应用

这是一份【通用版】2023届高考数学一轮复习计数原理与概率统计专练（11）回归分析及应用，共9页。试卷主要包含了2C，5万元B等内容，欢迎下载使用。
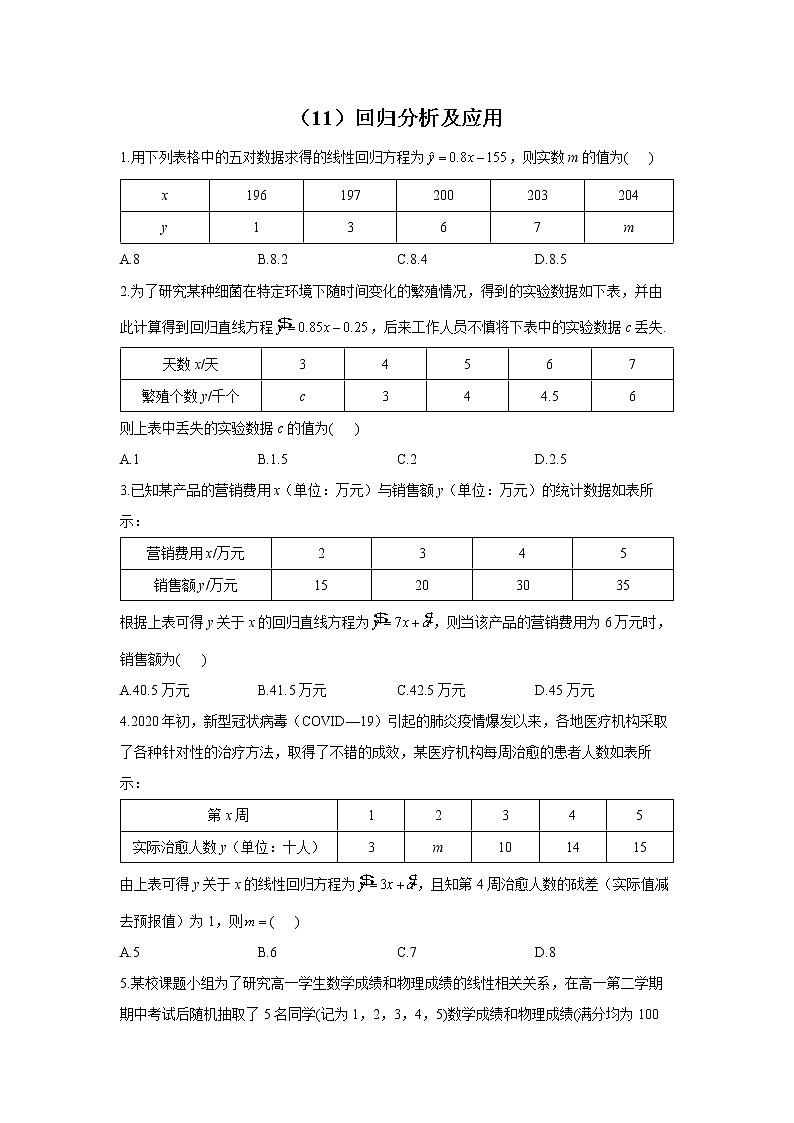
（11）回归分析及应用1.用下列表格中的五对数据求得的线性回归方程为，则实数m的值为(   )x196197200203204y1367mA.8 B.8.2 C.8.4 D.8.52.为了研究某种细菌在特定环境下随时间变化的繁殖情况，得到的实验数据如下表，并由此计算得到回归直线方程，后来工作人员不慎将下表中的实验数据c丢失.天数x/天34567繁殖个数y/千个c344.56则上表中丢失的实验数据c的值为(   )A.1 B.1.5 C.2 D.2.53.已知某产品的营销费用x（单位：万元）与销售额y（单位：万元）的统计数据如表所示：营销费用x/万元2345销售额y/万元15203035根据上表可得y关于x的回归直线方程为，则当该产品的营销费用为6万元时，销售额为(   )A.40.5万元 B.41.5万元 C.42.5万元 D.45万元4.2020年初，新型冠状病毒（COVID—19）引起的肺炎疫情爆发以来，各地医疗机构采取了各种针对性的治疗方法，取得了不错的成效，某医疗机构每周治愈的患者人数如表所示：第x周12345实际治愈人数y（单位：十人）3m101415由上表可得y关于x的线性回归方程为，且知第4周治愈人数的䂝差（实际值减去预报值）为1，则(   )A.5 B.6 C.7 D.85.某校课题小组为了研究高一学生数学成绩和物理成绩的线性相关关系，在高一第二学期期中考试后随机抽取了5名同学(记为1，2，3，4，5)数学成绩和物理成绩(满分均为100分)如表所示：学生代号12345数学成绩x7476767678物理成绩y7575767777则y关于x的线性回归方程为(   )A. B. C. D.6.某商场为了解销售活动中某商品销售量y与活动时间x之间的关系，随机统计了某5次销售活动中的商品销售量与活动时间，并制作了下表：活动时间x24568销售量y2540607080由表中数据，销售量y与活动时间x之间具有线性相关关系，算得线性回归方程为，则的值为(   )A.10.75 B.10.25 C.9.75 D.9.257.某种产品的广告支出x（单位：万元）与销售额y（单位：万元）之间的关系如下表：x24568y3040605070若已知y关于x的经验回归方程为，那么当广告支出为6万元时，随机误差的效应（残差）为_________万元（残差=观测值-预测值）(   )
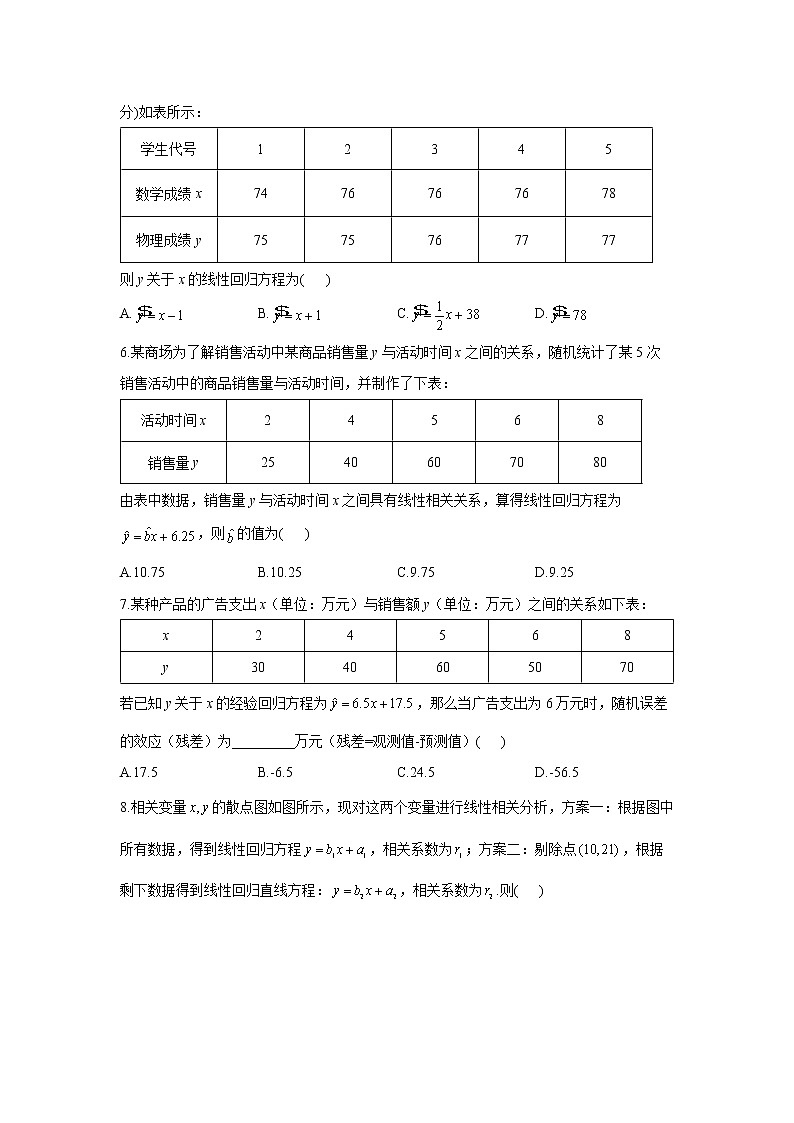
A.17.5 B.-6.5 C.24.5 D.-56.58.相关变量的散点图如图所示，现对这两个变量进行线性相关分析，方案一：根据图中所有数据，得到线性回归方程，相关系数为；方案二：剔除点，根据剩下数据得到线性回归直线方程：，相关系数为.则(   )
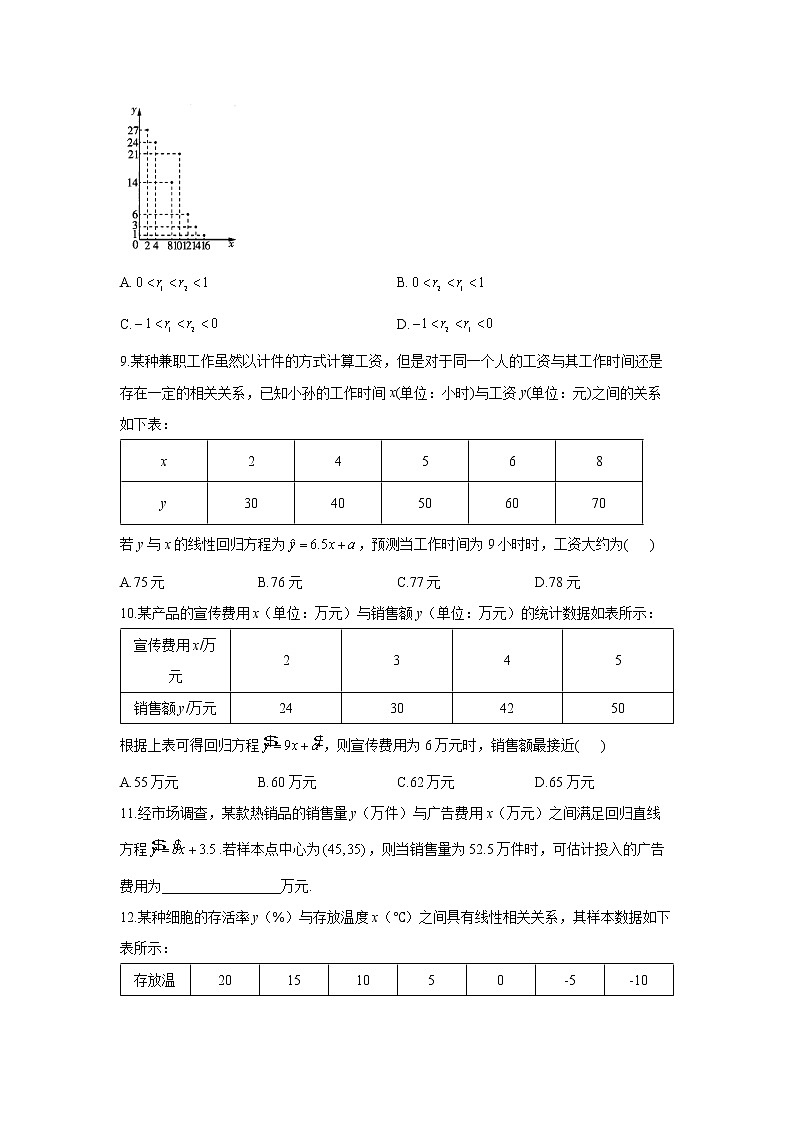
A.        B.   C.       D.9.某种兼职工作虽然以计件的方式计算工资，但是对于同一个人的工资与其工作时间还是存在一定的相关关系，已知小孙的工作时间x(单位：小时)与工资y(单位：元)之间的关系如下表：x24568y3040506070若y与x的线性回归方程为，预测当工作时间为9小时时，工资大约为(   )A.75元 B.76元 C.77元 D.78元10.某产品的宣传费用x（单位：万元）与销售额y（单位：万元）的统计数据如表所示：宣传费用x/万元2345销售额y/万元24304250根据上表可得回归方程，则宣传费用为6万元时，销售额最接近(   )A.55万元 B.60万元 C.62万元 D.65万元11.经市场调查，某款热销品的销售量y（万件）与广告费用x（万元）之间满足回归直线方程.若样本点中心为，则当销售量为52.5万件时，可估计投入的广告费用为_________________万元.12.某种细胞的存活率y（%）与存放温度x（℃）之间具有线性相关关系，其样本数据如下表所示：存放温度x/℃20151050-5-10存活率y/%6142633436063计算得，，，，并求得回归直线方程为.经核对，实验人员发现表中数据的对应值录入有误，更正为，则更正后的回归直线方程为_____________.13.已知某班学生每周用于物理学习的时间x（单位：h）与物理成绩y（单位：分）的几组数据如下：x24152319161120161713y92799789644783687159根据上表可得回归直线的斜率为3.53，则回归直线在y轴上的截距为___________（结果保留到0.1）.14.某互联网公司借助手机微信平台推广自己的产品，对今年前5个月的微信推广费用(单位：百万元)与利润额(单位：百万元)进行了初步统计，得到下列表格中的数据：2456830406070经计算，月微信推广费用与月利润额满足线性回归方程，则的值为_______________.15.已知高三某学生为了迎接高考，参加了学校的5次模拟考试，其中5次的模拟考试成绩如表所示，次数（x）12345考试成绩（y）498499497501505设变量x，y满足回归直线方程.（1）假如高考也符合上述的模拟考试的回归直线方程，高考看作第10次模拟考试，预测2021年的高考的成绩；（2）从上面的5次考试成绩中随机抽取3次，其中2次成绩都大于500分的概率.参考公式：回归直线方程中的斜率和截距的最小二乘估计公式分别为，.
答案以及解析1.答案：A解析：依题意，得，，回归直线必经过点，所以，解得，故选A.2.答案：D解析：本题考查回归直线方程在实际中的应用.由表中数据可得，，将点代入中，得，解得，所以丢失的实验数据c的值为2.5.故选D.3.答案：C解析：由题中表格数据可知，，因为回归直线一定经过点，所以，解得，所以回归直线方程为，将代入，得.故选C.4.答案：D解析：由第4周的残差为1，可知第4周的预报值为13，所以，解得，故.又回归直线必过样本点中心，且，所以，解得，故选D.5.答案：C解析：由表格中的数据，可得，，即数据的样本中心，因为满足回归直线方程，结合选项可得，即y关于x的线性回归方程为：，故选：C.6.答案：C解析：线性回归方程过样本中心点，，，.故选：C.7.答案：B解析：取，得， 当广告支出为6万元时，随机误差的效应（残差）为.故选B.8.答案：D解析：由散点图得负相关，所以，因为剔除点后，剩下点数据更具有线性相关性，更接近，所以.选D.9.答案：B解析：由表格数据知：，，，线性回归方程为，，即当工作时间为9小时时，工资大约为76元.故选：B.10.答案：B解析：，，由回归直线过样本点的中心，得，得，所以.当时，，所以销售额最接近60万元，故选B.11.答案：70解析：本题考查线性回归方程.依题意，将代入回归直线方程（提示：回归直线必过样本点中心），得，解得，所以回归直线方程为.令，得.12.答案：解析：由题意，知更正后，，，，所以，.所以更正后的回归直线方程为.13.答案：13.5
解析：由已知可得，.
设回归直线方程为，则，解得，所以回归直线在y轴上的截距为13.5.14.答案：50解析：由题中数据可得.因为线性回归方程对应的直线过点，所以，解得.15.答案：（1）预测2021年的高考成绩为511.2分（2）解析：（1）由表得，，.将点代入回归直线方程可得，解得，回归直线方程为.当时，，预测2021年的高考成绩为511.2分.（2）记“从5次考试成绩中选出3次成绩”为事件A，则事件A的情况有，，，，，，，，，，共10种情况，其中2次成绩都大于500分情况有，，，共3种情况，所求的概率.