数学八年级上册第十一章 三角形综合与测试练习题

这是一份数学八年级上册第十一章 三角形综合与测试练习题，共21页。试卷主要包含了如图，在中，，，求和的度数，请解答下列各题等内容，欢迎下载使用。
第11章 三角形 解答题

1．（2022·广东·塘厦初中八年级期末）如图，在中，AD是BC边上的高，CE平分，若，，求的度数．

2．（2022·广东云浮·八年级期末）若△ABC的三边长分别为m－2，2m＋1，8．
（1）求m的取值范围；
（2）若△ABC的三边均为整数，求△ABC的周长．
3．（2022·广东广州·八年级期末）已知一个正多边形一个内角等于一个外角的倍，求这个正多边形的边数．
4．（2022·广东河源·八年级期末）如图，E，G分别是AB，AC上的点，F，D是BC上的点，连接EF，AD，DG，已知，．

(1)求证：；
(2)若DG是∠ADC的平分线，，求∠B的度数．
5．（2022·广东湛江·八年级期末）如图，每个小正方形的边长均为1，点A和点B在小正方形的格点上．

(1)在图①中画出，使为直角三角形（要求点C在小正方形的格点上，画一个即可）．
(2)求图①中的面积．
6．（2022·广东汕尾·八年级期末）如图，△ABC中，AD平分∠BAC，P为AD延长线上一点，PE⊥BC于E，已知∠ACB＝80°，∠B＝24°，求∠P的度数．

7．（2022·广东东莞·八年级期末）如图，在中，，，求和的度数．

8．（2022·广东梅州·八年级期末）如图，AB∥CD，AE交CD于点C，DE⊥AE，垂足为E，∠A=37º，求∠D的度数

9．（2022·广东深圳·八年级期末）请解答下列各题：
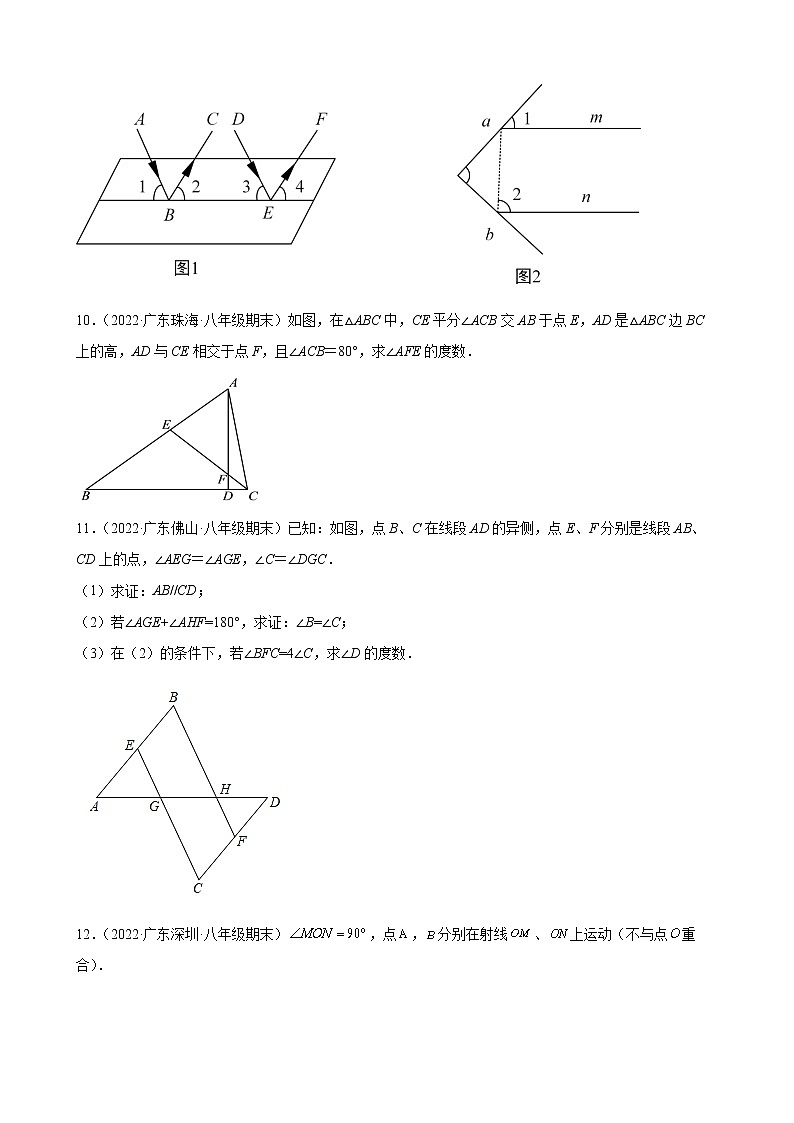
（1）阅读并回答：科学实验证明，平面镜反射光线的规律是：射到平面镜上的光线和被反射出的光线与平面镜所夹的角相等．如图1，一束平行光线与射向一个水平镜面后被反射，此时，．
①由条件可知：，依据是 ，，依据是 ．
②反射光线与平行，依据是 ．
（2）解决问题：如图2，一束光线射到平面镜上，被反射到平面镜上，又被镜反射，若射出的光线平行于，且，则 ； ．

10．（2022·广东珠海·八年级期末）如图，在△ABC中，CE平分∠ACB交AB于点E，AD是△ABC边BC上的高，AD与CE相交于点F，且∠ACB＝80°，求∠AFE的度数．

11．（2022·广东佛山·八年级期末）已知：如图，点B、C在线段AD的异侧，点E、F分别是线段AB、CD上的点，∠AEG＝∠AGE，∠C＝∠DGC．
（1）求证：AB//CD；
（2）若∠AGE+∠AHF=180°，求证：∠B=∠C；
（3）在（2）的条件下，若∠BFC=4∠C，求∠D的度数．

12．（2022·广东深圳·八年级期末），点，分别在射线、上运动（不与点重合）．

(1)如图①，、分别是和的平分线，随着点、点的运动，　　；
(2)如图②，若是的平分线，的反向延长线与的平分线交于点．
①若，则　　；
②随着点，的运动，的大小是否会变化？如果不变，求的度数；如果变化，请说明理由．
13．（2022·广东深圳·八年级期末）【问题背景】∠MON＝90°，点A、B分别在OM、ON上运动（不与点O重合）．


【问题思考】（1）如图①，AE、BE分别是∠BAO和∠ABO的平分线，随着点A、点B的运动，∠AEB＝　 　．
（2）如图②，若BC是∠ABN的平分线，BC的反向延长线与∠OAB的平分线交于点D．
①若∠BAO＝70°，则∠D＝　 　°．
②随着点A、B的运动，∠D的大小会变吗？如果不会，求∠D的度数；如果会，请说明理由；
【问题拓展】（3）在图②的基础上，如果∠MON＝a，其余条件不变，随着点A、B的运动（如图③），∠D＝　 　.（用含a的代数式表示）
14．（2022·广东河源·八年级期末）如图，已知，且与，分别交于A，B两点，点P在直线AB上.

（1）当点P在A，B两点之间运动时，求，，之间的数量关系，并说明理由.
（2）如果点P在A，B两点外侧运动，试探究，，之间的数量关系（点P与A，B不重合），并说明理由.
15．（2022·广东揭阳·八年级期末）如图，在△ABC中，D是BC上一点，AD=BD，∠C=∠ADC，∠BAC=57°，求∠DAC的度数．

16．（2022·广东韶关·八年级期末）探索归纳：


(1)如图1，已知为直角三角形，，若沿图中虚线剪去，则________．
(2)如图2，已知中，，剪去后成四边形，则__________．
(3)如图2，根据（1）与（2）的求解过程，请你归纳猜想与的关系是___________．
(4)如图3，若没有剪掉，而是把它折成如图3形状，试探究与的关系并说明理由．
17．（2022·广东清远·八年级期末）【探究】如图①，∠AFH和∠CHF的平分线交于点O，EG经过点O且平行于FH，分别与AB、CD交于点E、G．
(1)若∠AFH＝60°，∠CHF＝50°，则∠EOF＝_____度，∠FOH＝_____度．
(2)若∠AFH+∠CHF＝100°，求∠FOH的度数．
【拓展】如图②，∠AFH和∠CHI的平分线交于点O，EG经过点O且平行于FH，分别与AB、CD交于点E、G．若∠AFH+∠CHF＝α，直接写出∠FOH的度数．(用含a的代数式表示)


参考答案：
1．85°
【解析】
由高的定义可得出∠ADB＝∠ADC＝90，在△ACD中利用三角形内角和定理可求出∠ACB的度数，结合CE平分∠ACB可求出∠ECB的度数．由三角形外角的性质可求出∠AEC的度数，
解：∵AD是BC边上的高，
∴∠ADB＝∠ADC＝90．
在△ACD中，∠ACB＝180°﹣∠ADC﹣∠CAD＝180°﹣90°﹣20°＝70°．
∵CE平分∠ACB，
∴∠ECB＝∠ACB＝35°．
∵∠AEC是△BEC的外角，，
∴∠AEC＝∠B+∠ECB＝50°+35°＝85°．
答：∠AEC的度数是85°．
本题考查了三角形内角和定理、角平分线的定义以及三角形外角的性质，利用三角形内角和定理及角平分线的性质，求出∠ECB的度数是解题的关键．
2．（1）3＜m＜5；（2）19
【解析】
（1）直接利用三角形三边关系得出不等式组求出答案；
（2）利用m的取值范围得出m的值，进而得出答案．
（1）根据三角形的三边关系，
，
解得：3＜m＜5；
（2）因为△ABC的三边均为整数，且3＜m＜5，所以m＝4．
所以，△ABC 的周长为：（m−2）＋（2m＋1）＋8＝3m＋7＝3×4＋7＝19．
此题主要考查了三角形三边关系，正确得出不等式组是解题关键．
3．5
【解析】
多边形的内角和可以表示成（n-2）•180°，外角和是固定的360°，从而可根据一个正多边形的一个内角等于一个外角的列方程求解可得．
解：设此正多边形为正n边形．
∵正多边形的一个内角等于一个外角的，
∴此正多边形的内角和等于其外角和的，
∴×360°=（n-2）•180°，
解得n=5．
答：正多边形的边数为5．
本题考查正多边形的内角和与外角和．关键是记住内角和的公式与外角和的特征．
4．(1)见解析
(2)35°
【解析】
（1）由两直线平行，内错角相等得出，再根据题意可得出，最后根据同旁内角互补，两直线平行，即可得出；
（2）根据题意可求出的大小，再根据角平分线的定义，得出，最后根据两直线平行，同位角相等，即可求出的大小．
(1)
证明：∵，
∴．
又∵，．
∴．
(2)
∵，，
∴．
又∵DG是∠ADC的平分线，
∴．
∵，
∴．
本题考查平行线的判定和性质，角平分线的定义．利用数形结合的思想是解答本题的关键．
5．(1)见解析
(2)6
【解析】
（1）根据直角三角形的定义画出三角形即可．（答案不唯一）
（2）根据三角形面积公式求解即可．
(1)
解：如图①，△ABC即为所求．

(2)
解：图①中，△ABC的面积为：ACBC=×4×3=6．
本题考查作图-应用与设计，直角三角形的性质等知识，解题的关键是学会利用数形结合的思想解决问题．
6．∠P=28°．
【解析】
由题知：利用∠ACB＝80°，∠B＝24°，可求得∠ BAC；然后AD平分∠BAC，可得∠CAD；利用△ACD，可得∠PDE，即可求解．
在△ABC中，∠ACB＝80°，∠B＝24°，
∴∠BAC＝180°﹣∠ACB﹣∠B＝76°.
∵AD平分∠BAC，
∴∠CAD＝∠BAC＝38°．
在△ACD中，∠ACD＝80°，∠CAD＝38°，
∴∠ADC＝180°﹣∠ACD﹣∠CAD＝62°，
∴∠PDE＝∠ADC＝62°．
∵PE⊥BC于E，
∴∠PED＝90°，
∴∠P＝180°﹣∠PDE﹣∠PED＝28°；
∴ ∠P＝28°．
本题考查角平分线、三角形内角和的定义和性质，关键在题目需要对所求角进行不断的转换分析，进而与已知量结合进行求解．
7．∠B＝77°，∠C＝
【解析】
根据等腰三角形的性质及三角形内角和定理可求出∠B和∠ADB的度数，利用三角形外角性质即可求出∠C的度数．
解：∵AB＝AD，
∴∠B＝∠ADB＝×（180°﹣26°）＝77°，
∵AD＝DC，
∴∠C=∠DAC，
∴∠C＝∠ADB＝×77°＝．
本题考查等腰三角形的性质及三角形外角的性质，掌握等边对等角、三角形三个内角和等于180°和三角形的一个外角等于和它不相邻的两个内角的和是解题关键．
8．53°
【解析】
解: ∵AB∥CD, ∠A=37º,
∴∠ECD=∠A=37º
∵DE⊥AE,
∴∠D=90º–∠ECD=90º–37º=53º
9．（1）①两直线平行，同位角相等；等量代换．②同位角相等，两直线平行．（2）84°；90°；
【解析】
（1）根据平行线的判定与性质逐一求解可得；
（2）根据入射角等于反射角得出∠1=∠4，∠5=∠7，求出∠6，根据平行线性质即可求出∠2，求出∠5，根据三角形内角和求出∠3即可．
解：（1）①由条件可知：∠1=∠3，依据是：两直线平行，同位角相等；
∠2=∠4，依据是：等量代换；
②反射光线BC与EF平行，依据是：同位角相等，两直线平行；
故答案为：①两直线平行，同位角相等；等量代换．②同位角相等，两直线平行．
（2）如图，

∵∠1=42°，
∴∠4=∠1=42°，
∴∠6=180°42°42°=96°，
∵m∥n，
∴∠2+∠6=180°，
∴∠2=84°，
∴∠5=∠7=，
∴∠3=180°48°42°=90°．
故答案为：84°；90°；
本题考查了平行线的性质和判定，三角形的内角和定理的应用，熟练掌握平行线的判定与性质是解题的关键．
10．∠AFE=50°．
【解析】
根据CE平分∠ACB，∠ACB＝80°，得出∠ECB=，根据高线性质得出∠ADC=90°，根据三角形内角和得出∠DFC=180°-∠ADC-∠ECB=180°-90°-40°=50°，利用对顶角性质得出∠AFE=∠DFC=50°即可．
解：∵CE平分∠ACB，∠ACB＝80°，
∴∠ECB=，
∵AD是△ABC边BC上的高，AD⊥BC，
∴∠ADC=90°，
∴∠DFC=180°-∠ADC-∠ECB=180°-90°-40°=50°，
∴∠AFE=∠DFC=50°．
本题考查角平分线定义，垂线性质，三角形内角和，对顶角性质，掌握角平分线定义，垂线性质，三角形内角和，对顶角性质是解题关键．
11．（1）见解析；（2）见解析；（3）108°
【解析】
（1）根据对顶角相等结合已知条件得出∠AEG＝∠C，根据内错角相等两直线平行即可证得结论；
（2）由∠AGE+∠AHF=180°等量代换得∠DGC+∠AHF=180°可判断EC//BF，两直线平行同位角相等得出∠B=∠AEG，结合（1）得出结论；
（3）由（2）证得EC//BF，得∠BFC+∠C=180°，求得∠C的度数，由三角形内角和定理求得∠D的度数．
证明：（1）∵∠AEG=∠AGE，∠C=∠DGC，∠AGE=∠DGC
∴∠AEG=∠C     
∴AB//CD
（2）∵∠AGE=∠DGC，∠AGE+∠AHF=180°
∴∠DGC+∠AHF=180°
∴EC//BF   
∴∠B=∠AEG
由（1）得∠AEG=∠C     
∴∠B=∠C
（3）由（2）得EC//BF
∴∠BFC+∠C=180°
∵∠BFC=4∠C     
∴∠C=36°     
∴∠DGC=36°
∵∠C+∠DGC+∠D=180°     
∴∠D=108°
此题考查了平行线的判定与性质，三角形内角和定理，熟记“内错角相等，两直线平行”、“同旁内角互补，两直线平行”及“两直线平行，同旁内角互补”是解题的关键．
12．(1)135
(2)①45；②不变，45°
【解析】
（ 1）根据三角形的内角和定理和角平分线的定义即可得到结论；
（2 ）①根据三角形的内角和定理和角平分线的定义即可得到结论；
②由①的思路可得结论．
(1)
解：（ 1）直线与直线垂直相交于，
，
，
、分别是和角的平分线，
，，
，
；
故答案为：135；
(2)
①，，
，
，
是的平分线，
，
平分，
，
，
故答案为：45；
②的度数不随、的移动而发生变化，
设，
平分，
，
，
，
平分，
，
，
．
本题考查了三角形的内角和定理，角平分线的定义，熟练掌握三角形的内角和定理是解题的关键．
13．（1）135°；（2）①45；②∠D的度数不随着点A、B的运动而发生变化；∠D=45°；（3）．
【解析】
（1）根据三角形的内角和定理和角平分线的定义即可得到结论；
（2）①根据三角形的内角和定理和角平分线的定义进行计算即可得到结论；②设∠BAD=，再根据三角形的内角和定理和角平分线的定义进行计算即可得到结论；
（3）设 而 再利用角平分线的含义与三角形的外角的性质分别表示 再利用三角形的内角和定理可得答案．
解：（1） ，
∴∠OAB+∠OBA=90°，
∵AE、BE分别是∠BAO和∠ABO角的平分线，
∴∠BAE=，∠ABE=，
∴∠BAE+∠ABE==45°，
∴∠AEB=135°； 故答案为：135°；
（2）①∵∠AOB=90°，∠BAO=，
∴∠ABO=，
∴∠ABN=，
∵BC是∠ABN的平分线，
∴∠OBD=∠CBN=，
∵AD平分∠BAO， ∴∠DAB=，
∴∠D=180°-∠ABD-∠BAD =，
故答案为：；
②∠D的度数不随A、B的移动而发生变化， 设∠BAD=，
∵AD平分∠BAO，
∴∠BAO=，
∵∠AOB=90°，
∴∠ABN=180°-∠ABO=∠AOB+∠BAO=，
∵BC平分∠ABN， ∴∠ABC=，
∵∠ABC=180°-∠ABD=∠D+∠BAD，
∴∠D=∠ABC-∠BAD=；
（3）设 而
∵∠BAO与的平分线交于点

而



故答案为：
本题考查了三角形的内角和定理，三角形的外角的性质，角平分线的定义，熟练掌握三角形的内角和定理与三角形的外角的性质是解题的关键．
14．（1），见解析；（2）或，见解析.
【解析】
（1）过点P作l1的平行线，根据平行线的性质进行解题；
（2）当点P在下侧时，过点P作l1的平行线PQ，由平行线的性质可得出l1∥l2∥PQ，由此即可得出结论．
（1）.
理由如下：如图所示，过点P作．
，
，
，．
，
．

（2）或．
理由如下：当点P在下侧时，过点P作的平行线PQ，如图所示，

，
，
，，
．
当点P在上侧时，如图所示，


，
，又，
．
本题考查的是平行线的性质、三角形的外角性质，根据题意作出辅助线是解答此题的关键．
15．16°.
【解析】
试题分析：根据等腰三角形的性质得到∠B=∠BAD，由三角形的外角的性质得到∠ADC=∠B+∠BAD=2∠B，于是得到∠C=2∠B，根据三角形的内角和得到∠B+∠C=3∠B=180°-∠BAC=41°，根据得到结论．
试题解析：∵AD=BD，
∴∠B=∠BAD，
∵∠ADC=∠B+∠BAD=2∠B，
∴∠C=2∠B，
∵∠BAC=57°，
∴∠B+∠C=3∠B=180°-∠BAC=41°，
∴∠ADC=∠C=82°，
∴∠DAC=16°．
16．(1)270
(2)220
(3)
(4)，理由见解析
【解析】
(1)利用三角形的外角定理及直角三角形的性质求解；
(2)利用三角形的外角等于与它不相邻的两个内角和求解；
(3)根据(1)、(2)中思路即可求解；
(4)根据折叠对应角相等，得到，，进而求出，，最后利用即可求解．
(1)
解：如下图所示：


在△AEF中，由外角性质可知：∠1=∠A+∠EFA=90°+∠EFA，∠2=∠A+∠AEF=90°+∠AEF，
∴∠1+∠2=(90°+∠EFA)+( 90°+∠AEF)=180°+∠EFA+∠AEF，
∵△ABC为直角三角形，
∴∠A=90°，∠EFA+∠AEF=180°-∠A=90°，
∴∠1+∠2=180°+90°=270°．
(2)
解：如下图所示：


在△AEF中，由外角性质可知：∠1=∠A+∠EFA，∠2=∠A+∠AEF，
∴∠1+∠2=(∠A+∠EFA)+( ∠A+∠AEF)=(∠A +∠EFA+∠AEF)+∠A=180°+40°=220°．
(3)
解：由(1)、(2)中思路，由三角形外角性质可知：
∠1=∠A+∠EFA，∠2=∠A+∠AEF，
∴∠1+∠2=(∠A+∠EFA)+( ∠A+∠AEF)=(∠A +∠EFA+∠AEF)+∠A=180°+∠A，
∴与的关系是：∠1+∠2=180°+∠A．
(4)
解：与的关系为：，理由如下：
如图，


∵是由折叠得到的，
∴，，
∴，，
∴，
又∵，
∴，
∴与的关系．
主要考查了折叠的性质及三角形的内角和外角之间的关系：三角形的外角等于与它不相邻的两个内角和、三角形的内角和是180度．求角的度数常常要用到“三角形的内角和是180°”这一隐含的条件．
17．【探究】（1）30，125；（2）∠FOH＝130°；【拓展】∠FOH＝90°﹣α．
【解析】
（1）先根据角平分线的定义求出∠OFH，∠FHO 的度数，再根据三角形的内角和定理求出∠FOH的度数；
（2）先根据角平分线的定义求出∠OFH+∠FHO 的度数，再根据三角形的内角和定理求出∠FOH的度数；
（拓展）     先根据角平分线的定义求出∠OFH＝∠AFH，∠OHI＝∠CHI＝（180°-∠CHF），再根据两直线平行内错角相等得∠FOH＝∠OHI﹣∠OFH即可．
探究
（1）∵∠AFH＝60°，OF平分∠AFH，
∴∠OFH＝30°，
又∵EG∥FH，
∴∠EOF＝∠OFH＝30°；
∵∠CHF＝50°，OH平分∠CHF，
∴∠FHO＝25°，
∴△FOH中，∠FOH＝180°﹣∠OFH﹣∠OHF＝125°；
故答案为30，125；
（2）∵FO平分∠AFH，HO平分∠CHF，
∴∠OFH＝∠AFH，∠OHF＝∠CHF．
∵∠AFH+∠CHF＝100°，
∴∠OFH+∠OHF＝（∠AFH+∠CHF）＝×100°＝50°．
∵EG∥FH，
∴∠EOF＝∠OFH，∠GOH＝∠OHF．
∴∠EOF+∠GOH＝∠OFH+∠OHF＝50°．
∵∠EOF+∠GOH+∠FOH＝180°，
∴∠FOH＝180°﹣（∠EOF+∠GOH ）＝180°﹣50°＝130°．
拓展∵∠AFH和∠CHI的平分线交于点O，
∴∠OFH＝∠AFH，∠OHI＝∠CHI，
∴∠FOH＝∠OHI﹣∠OFH
＝（∠CHI﹣∠AFH）
＝（180°﹣∠CHF﹣∠AFH）
＝（180°﹣α）
＝90°﹣α．
本题考查角平分线的定义、三角形的内角和定理、平行线的性质，解题的关键是熟练应用．