初中人教版第十二章 全等三角形综合与测试综合训练题

这是一份初中人教版第十二章 全等三角形综合与测试综合训练题，共34页。

第12章 全等三角形 选择题

1．（2022·广东广州·八年级期末）如图是两个全等三角形，图中的字母表示三角形的边长，则∠1的度数是（       ）

A．115° B．65° C．40° D．25°
2．（2022·广东·塘厦初中八年级期末）如图，在中，，，AD平分交BC于点D，在AB上截取，则的度数为（       ）


A．30° B．20° C．10° D．15°
3．（2022·广东·肇庆市华南师范大学附属肇庆学校八年级期末）如图，，点A和点B，点C和点D是对应点．如果AB=6厘米，BD=5厘米，AD=4厘米，那么BC的长是（     ）

A．6 cm B．5 cm C．4 cm D．不能确定
4．（2022·广东肇庆·八年级期末）如图，ABC中，AD平分∠BAC，AB＝4，AC＝2，若ACD的面积等于3，则ABD的面积为（       ）

A． B．4 C．6 D．12
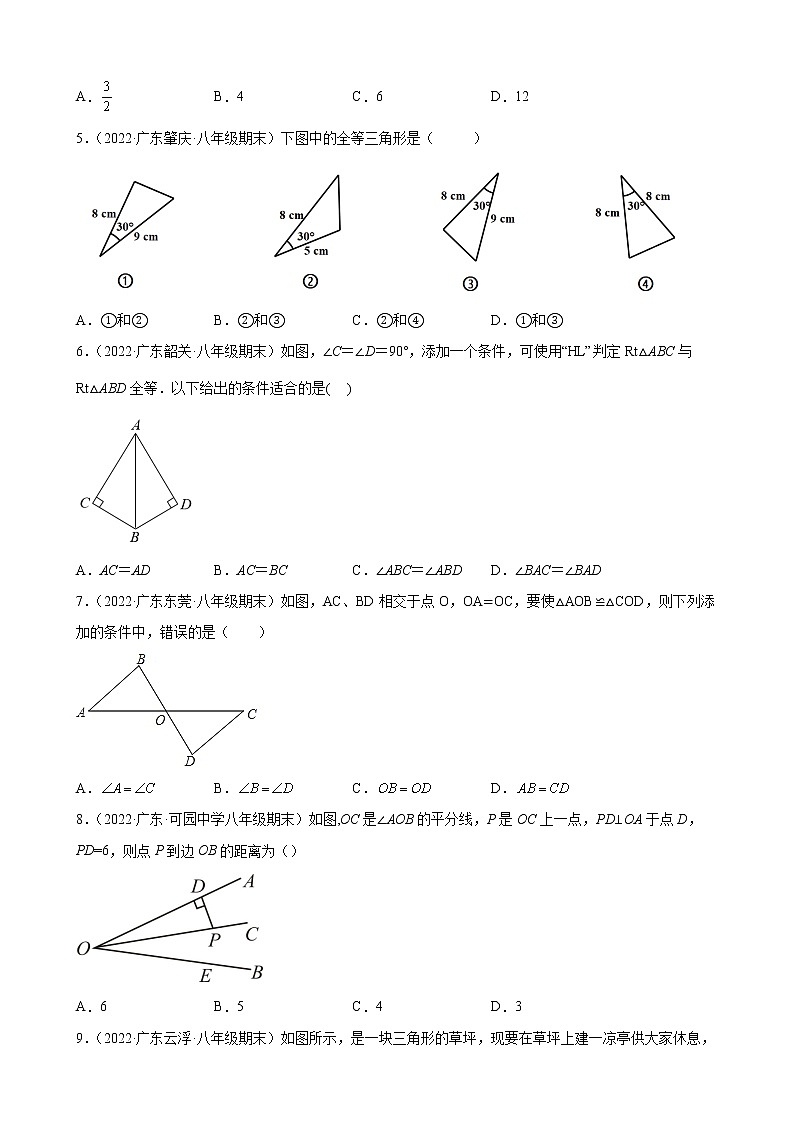
5．（2022·广东肇庆·八年级期末）下图中的全等三角形是（       ）

A．①和② B．②和③ C．②和④ D．①和③
6．（2022·广东韶关·八年级期末）如图，∠C＝∠D＝90°，添加一个条件，可使用“HL”判定Rt△ABC与Rt△ABD全等．以下给出的条件适合的是(   )

A．AC＝AD B．AC＝BC C．∠ABC＝∠ABD D．∠BAC＝∠BAD
7．（2022·广东东莞·八年级期末）如图，AC、BD相交于点O，OA=OC，要使△AOB≌△COD，则下列添加的条件中，错误的是（　　）

A． B． C． D．
8．（2022·广东·可园中学八年级期末）如图,OC是∠AOB的平分线，P是OC上一点，PD⊥OA于点D，PD=6，则点P到边OB的距离为（）

A．6 B．5 C．4 D．3
9．（2022·广东云浮·八年级期末）如图所示，是一块三角形的草坪，现要在草坪上建一凉亭供大家休息，要使凉亭到草坪三条边的距离相等，凉亭的位置应选在（       ）


A．的三条中线的交点
B．三边的垂直平分线的交点
C．三条角平分线的交点
D．三条高所在直线的交点
10．（2022·广东云浮·八年级期末）如图，在和中，，，，则（       ）

A．30° B．40° C．50° D．60°
11．（2022·广东汕尾·八年级期末）如图所示，，，要使，需添加条件是（       ）


A． B． C． D．
12．（2022·广东阳江·八年级期末）如图，若△ABC≌△DEF，B、E、C、F在同一直线上，BC＝7，EC＝4，则CF的长是（　　）

A．2 B．3 C．5 D．7
13．（2022·广东广州·八年级期末）如图，已知∠1＝∠2，要得到结论ABC≌ADC，不能添加的条件是（       ）

A． BC＝DC B．∠ACB＝∠ACD C．AB＝AD D．∠B＝∠D
14．（2022·广东·东莞市光明中学八年级期末）如图，中，，，以点为圆心，任意长为半径作弧，分别交、于和，再分别以点、为圆心，大于二分之一为半径作弧，两弧交于点，连接并延长交于点，于，，则的面积为　　

A．4 B．5 C．9 D．10
15．（2022·广东汕头·八年级期末）如图，已知AB＝AC，CD⊥AB于点D，BE⊥AC于点E，CD与BE相交于点F，连接AF，则图中共有（            ）对全等三角形

A．3 B．4 C．5 D．6
16．（2022·广东韶关·八年级期末）如图，已知，要得到，还需从下列条件中补选一个，则错误的选法是（       ）


A． B． C． D．
17．（2022·广东潮州·八年级期末）如图，在△ABC中，BC=10，CD是∠ACB的平分线．若P，Q分别是CD和AC上的动点，且△ABC的面积为24，则PA+PQ的最小值是（       ）

A． B．4 C． D．5
18．（2022·广东佛山·八年级期末）下列命题为真命题的是（　　）
A．同位角相等 B．三角形的外角等于两个内角的和 C．相等的角是对顶角 D．全等三角形的对应角相等
19．（2022·广东广州·八年级期末）如图，在△ABC中，∠B＝90°，AD平分∠BAC，交BC于点D，BC＝8cm，BD：CD＝3：4，则点D到AC的距离为（　　）cm．

A．3 B．4 C． D．
20．（2022·广东汕尾·八年级期末）如图，已知点，，，在一条直线上，，，那么添加下列一个条件后，仍无法判定的是（       ）

A． B． C． D．
21．（2022·广东广州·八年级期末）如图，Rt△ABC中，∠C＝90°，AD平分∠BAC，交BC于点D，CD＝6，AB＝12，则△ABD的面积是（       ）

A．18 B．24 C．36 D．72
22．（2022·广东东莞·八年级期末）如图，在△ABC和△DEF中，∠A＝∠D，AF＝DC，添加下列条件中的一个仍无法证明△ABC≌△DEF的是（　　）

A．BC＝EF B．AB＝DE C．∠B＝∠E D．∠ACB＝∠DFE
23．（2022·广东云浮·八年级期末）如图是用直尺和圆规作一个角等于已知角的示意图，说明的依据是（       ）

A． B． C． D．
24．（2022·广东珠海·八年级期末）已知图中的两个三角形全等，则等于（       ）

A． B． C． D．
25．（2022·广东惠州·八年级期末）如图，已知，，增加哪个条件不能保证的是（     ）

A． B． C． D．
26．（2022·广东广州·八年级期末）已知图中的两个三角形全等，图中的字母表示三角形的边长，则∠1等于（　　）

A．72° B．60° C．50° D．58°
27．（2022·广东潮州·八年级期末）如图，已知△ABE≌△ACD，下列选项中不能被证明的等式是(       )

A．AD＝AE B．DB＝AE C．DF＝EF D．DB＝EC
28．（2022·广东东莞·八年级期末）已知：如图，CD⊥AB，BE⊥AC，垂足分别为D、E，BE、CD相交于O点，∠1＝∠2．图中全等的三角形共有（       ）

A．4对 B．3对 C．2对 D．1对
29．（2022·广东广州·八年级期末）如图，△ABC≌△ADE，点D在BC上，且∠B＝60°，则∠EDC的度数等于（       ）

A．30° B．45° C．60° D．75°
30．（2022·广东茂名·八年级期末）如图，在△ABC中，∠ABC和∠ACB的平分线相交于点O，过点O作EF∥BC交AB于点E，交AC于点F，过点O作OD⊥AC于点D，下列四个结论：①BE＝EF﹣CF；②∠BOC＝90°+∠A；③点O到△ABC各边的距离相等；④设OD＝m，AE+AF＝n，则S△AEF＝mn，其中正确结论的个数有（　　）

A．1个 B．2个 C．3个 D．4个
31．（2022·广东江门·八年级期末）如图，在四边形ABCD中，∠A＝90°，AD＝6，连接BD，BD⊥CD，∠ADB＝∠C．若P是BC边上一动点，则DP长的最小值为（　　）

A．4 B．6 C．3 D．12
32．（2022·广东东莞·八年级期末）如图所示，OP平分∠AOB，PA⊥OA于点A，PB⊥OB于点B．下列结论中,不一定成立的是(     )

A．PA=PB B．PO平分∠APB C．OA=OB D．AB垂直平分OP
33．（2022·广东·可园中学八年级期末）如图，已知∠ABC＝∠DEF，AB＝DE，添加以下条件，不能判定△ABC≌△DEF的是（　　）

A．∠A＝∠D B．∠ACB＝∠DFE C．AC＝DF D．BE＝CF
34．（2022·广东江门·八年级期末）如图，在△ABC 和△DEF 中，AC=DF，AB=DE，添加下列一个条件后，仍然不能证明△ABC≌△DEF，这个条件是（ ）

A．∠A=∠D B．BE=CF C．∠ACB=∠DFE=90° D．∠B=∠DEF
35．（2022·广东广州·八年级期末）如图，已知△ABC的六个元素，则下列甲、乙、丙三个三角形中和△ABC全等的图形是（       ）

A．甲乙 B．甲丙 C．乙丙 D．乙
36．（2022·广东广州·八年级期末）如图，与相交于，且，如果添加一个条件还不能判定≌，则添加的这个条件是（     ）

A． B． C． D．
37．（2022·广东·东莞市光明中学八年级期末）如图，已知OA＝OB，OC＝OD，AD和BC相交于点E，则图中共有全等三角形的对数（　　）

A．2对 B．3对 C．4对 D．5对
38．（2022·广东·湛江市坡头区龙头中学八年级期末）以下说法正确的是   (        )
①一条直角边和斜边上的高对应相等的两个直角三角形全等；②有两条边相等的两个直角三角形全等；③有一边相等的两个等边三角形全等；④两边和其中一边的对角对应相等的两个三角形全等．
A．①② B．②④ C．①③ D．①③④
39．（2022·广东湛江·八年级期末）小明同学在学习了全等三角形的相关知识后发现，只用两把完全相同的长方形直尺就可以作出一个角的平分线．如图：一把直尺压住射线OB，另一把直尺压住射线OA并且与第一把直尺交于点P，小明说：“射线OP就是∠BOA的角平分线．”他这样做的依据是(　　)

A．角的内部到角的两边的距离相等的点在角的平分线上
B．角平分线上的点到这个角两边的距离相等
C．三角形三条角平分线的交点到三条边的距离相等
D．以上均不正确
40．（2022·广东河源·八年级期末）如图，在△ABC中，∠C=90°，按以下步骤作图：①以点A为圆心、适当长为半径作圆弧，分别交边AC、AB于点M、N；②分别以点M和点N为圆心、大于MN的长为半径作圆弧，在∠BAC内，两弧交于点P；③作射线AP交边BC于点D，若CD=4，AB=15，则△ABD的面积是（       ）

A．15 B．30 C．45 D．60
41．（2022·广东肇庆·八年级期末）如图，AD是△ABC的中线，E，F分别是AD和AD延长线上的点，且DE=DF，连结BF，CE.下列说法：①△ABD和△ACD面积相等；②∠BAD=∠CAD；③△BDF≌△CDE；④BF∥CE；⑤CE=AE.其中正确的有（　　）

A．1个 B．2个 C．3个 D．4个
42．（2022·广东汕尾·八年级期末）如图，△ABC≌△DCB，点A、B的对应顶点分别为点D、C，如果AB＝7cm，BC＝12cm，AC＝9cm，那么BD的长是（     ）．

A．7cm B．9cm C．12cm D．无法确定
43．（2022·广东惠州·八年级期末）如图，已知和都是等腰三角形，，交于点F，连接，下列结论：①；②；③平分；④．其中正确结论的个数有（       ）

A．1个 B．2个 C．3个 D．4个

参考答案：
1．C
【解析】
根据三角形内角和定理求出∠2，根据全等三角形的性质解答即可．
解：由三角形内角和定理得，∠2=180°-115°-25°=40°，
∵两个三角形全等，
∴∠1=∠2=40°，
故选：C．

本题考查的是全等三角形的性质、三角形内角和定理，掌握全等三角形的对应角相等是解本题的关键．
2．B
【解析】
利用已知条件证明△ADE≌△ADC（SAS），得到∠DEA＝∠C，根据外角的性质可求的度数．
解：∵AD是∠BAC的平分线，
∴∠EAD＝∠CAD
在△ADE和△ADC中，
，
∴△ADE≌△ADC（SAS），
∴∠DEA＝∠C，
∵，∠DEA＝∠B +，
∴；
故选：B
本题考查了全等三角形的性质与判定，解决本题的关键是证明△ADE≌△ADC．
3．C
【解析】
根据全等三角形的性质可直接进行求解．
解：∵，AD=4厘米，
∴；
故选C．
本题主要考查全等三角形的性质，熟练掌握全等三角形的性质是解题的关键．
4．C
【解析】
过D点作DE⊥AB于E，DF⊥AC于F，如图，利用角平分线的性质得DE=DF，再根据三角形面积公式，利用S△ACD=•DF•AC=3得到DF=DE=3，然后利用三角形面积公式计算S△ABD．
解：过D点作DE⊥AB于E，DF⊥AC于F，如图，

∵AD平分∠BAC，
∴DE=DF，
∵S△ACD=•DF•AC=3，
∴DF==3，
∴DE=3．
∴S△ABD=•DE•AB=×3×4=6．
故选：C．
本题考查了角平分线的性质：角的平分线上的点到角的两边的距离相等．
5．D
【解析】
根据两边及其夹角对应相等两个三角形全等，逐项判断，即可求解．
解：A、①和②只有一边一角对应相等，不能证明全等，故本选项错误，不符合题意；
B、②和③只有一边一角对应相等，不能证明全等，故本选项错误，不符合题意；
C、②和④只有一边一角对应相等，不能证明全等，故本选项错误，不符合题意；
D、①和③两边及其夹角对应相等，能证明全等，故本选项正确，符合题意；
故选：D
本题主要考查了全等三角形的判定定理，熟练掌握两边及其夹角对应相等两个三角形全等是解题的关键．
6．A
【解析】
由已知两三角形为直角三角形，且斜边为公共边，若利用HL证明两直角三角形全等，需要添加的条件为一对直角边相等，即BC=BD或AC=AD.
解： 需要添加条件为：BC= BD或AC= AD,理由为:
若添加的条件为：BC= BD
在Rt△ABC与Rt△ABD中,
 
∴Rt△ABC≌Rt△ABD(HL) ;
若添加的条件为：AC=AD
在Rt△ABC与Rt△ABD中,

∴Rt△ABC≌Rt△ABD( HL).
故选：A.
本题考查了利用HL公理判定直角三角形全等，熟练运用HL公理是解题的关键
7．D
【解析】
观察图形可知：已有一角一边对应相等．根据三角形全等的判定方法解答．
解：∵OA=OC，∠AOB=∠COD（对顶角相等），
∴A、如果添加∠A=∠C，则可根据ASA判定△AOB≌△COD；
B、如果添加∠B=∠D，则可根据AAS判定△AOB≌△COD；
C、如果添加OB=OD，则可根据SAS判定△AOB≌△COD；
D、如果添加 AB=CD，则根据SSA不能判定△AOB≌△COD．
故选D．
本题考查全等三角形的判定，熟练掌握判定方法是关键．
8．A
【解析】
如图，过点P作PE⊥OB于点E，

∵OC是∠AOB的平分线，PD⊥OA于D，
∴PE=PD，
∵PD=6，
∴PE=6，即点P到OB的距离是6．
故选A．
考点：角平分线的性质
9．C
【解析】
根据题意，想到角平分线的性质：角平分线上的点到角两边的距离相等，所以要选角平分线的交点．
∵要使凉亭到草坪三边的距离相等，
∴凉亭应在三条角平分线的交点处．
故选：C．
本题考查了角平分线的性质，需要注意区分三角形中线的交点、高的交点、垂直平分线的交点以及角平分线的交点之间的区别．
10．D
【解析】
由题意可证，有，由三角形内角和定理得，计算求解即可．
解：∵
∴△ABC和△ADC均为直角三角形
在和中
∵
∴
∴
∵
∴
故选D．
本题考查了三角形全等，三角形的内角和定理．解题的关键在于找出角度的数量关系．
11．D
【解析】
根据已知条件是两个三角形的两组对应边，所以需要添加的条件必须能得到这两边的夹角相等，整理得到角的可能情况，然后选择答案即可．
∵AB=BD，BC=BE，
∴要使△ABE≌△DBC，需添加的条件为∠ABE=∠DBC，
又∠ABE-∠DBE=∠DBC-∠DBE，
即∠ABD=∠CBE，
∴可添加的条件为∠ABE=∠DBC或∠ABD=∠CBE．
综合各选项，D选项符合．
故选：D．
本题考查了全等三角形的判定，根据两边确定出需添加的条件必须是这两边的夹角是解题的关键．
12．B
【解析】
根据全等三角形的性质求出EF，结合图形计算，得到答案．
解：∵△ABC≌△DEF，BC＝7，
∴EF＝BC＝7，
∴CF＝EF﹣EC＝3，
故选：B．
本题考查的是全等三角形的性质，掌握全等三角形的对应边相等是解题的关键．
13．A
【解析】
根据全等三角形的判定方法，逐项判断即可求解．
解：根据题意得： ，∠1＝∠2，
A、当BC＝DC时，是边边角，不能得到结论ABC≌ADC，故本选项符合题意；
B、当∠ACB＝∠ACD时，是角边角，能得到结论ABC≌ADC，故本选项不符合题意；
C、当AB＝AD时，是边角边，能得到结论ABC≌ADC，故本选项不符合题意；
D、当∠B＝∠D时，是角角边，能得到结论ABC≌ADC，故本选项不符合题意；
故选：A
本题主要考查了全等三角形的判定，熟练掌握全等三角形的判定方法——边角边、角边角、角角边、边边边是解题的关键．
14．B
【解析】
作GM⊥AB于M，如图，先利用基本作图得到AG平分∠BAC，再根据角平分线的性质得到GM=GH=2，然后根据三角形面积公式计算．
作GM⊥AB于M，如图，

由作法得AG平分∠BAC，
而GH⊥AC，GM⊥AB，
∴GM=GH=2，
∴S△ABG=×5×2=5．
故选：B．
本题考查了角平分线的性质：角的平分线上的点到角的两边的距离相等，解题的关键是看出题干中的尺规作图是作角平分线．
15．C
【解析】
由题意可直接利用“AAS”证明，得出，，．即还可利用“HL”证明，得出．从而可利用“ASA”证明，得出．进而可利用“AAS”证明，得出，最后可利用“HL”证明，由此即可选择．
由题意可知在和中，，
∴，
∴，，，
∴在和中，，
∴，
∴，即，
∴在和中，，
∴，
∴，
∴在和中，，
∴，
∴，
∴在和中，，
∴．
综上，可知图中共有5对全等三角形．
故选C．
本题考查全等三角形的判定和性质．熟练掌握全等三角形的判定方法，证明三角形全等是解答本题的关键．
16．B
【解析】
利用全等三角形的判定方法依次分析即可．
A.AB＝AC，∠1＝∠2，AD＝AD，利用SAS可判定△ABD≌△ACD，故A不符合题意
B.DB＝DC，∠1＝∠2，AD＝AD，利用SSA不可判定△ABD≌△ACD，故B符合题意；
C.∠ADB＝∠ADC，∠1＝∠2，AD＝AD，利用ASA可判定△ABD≌△ACD，故C不符合题意；
D.∠B＝∠C，∠1＝∠2，AD＝AD，利用AAS可判定△ABD≌△ACD，故D不符合题意．
故选：B．
本题考查全等三角形的判定．熟练掌握SSS、SAS、ASA、AAS是本题解题的关键．
17．C
【解析】
过点A作AG⊥BC交于G，交CD于P点，过点P作PQ⊥AC交于Q点，当A、P、G三点共线时，AP+PQ的值最小，求出AG的长即为所求．
解：过点A作AG⊥BC交于G，交CD于P点，过点P作PQ⊥AC交于Q点，

∵CD是∠ACB的平分线，
∴PG=PQ，
∴PA+PQ=AP+PG≥AG，
∴当A、P、G三点共线时，AP+PQ的值最小，
∵BC=10，△ABC的面积为24，
∴AG=，
∴AP+PQ的最小值为，
故选：C．
本题考查最短距离的求法，熟练掌握角平分线的性质，垂线段最短是解题的关键．
18．D
【解析】
由平行线的性质可判断A，由三角形的外角的性质可判断B，由对顶角的定义可判断C，由全等三角形的性质可判断D，从而可得答案.
解：两直线平行，同位角相等，故A不符合题意；
三角形的外角等于和它不相邻的两个内角的和，故B不符合题意；
相等的角不一定是对顶角，故C不符合题意；
全等三角形的对应角相等，是真命题，故D符合题意；
故选D
本题考查的是平行线的性质，三角形的外角的性质，对顶角的定义，全等三角形的性质，命题真假的判断，掌握“判断真假命题的方法”是解本题的关键.
19．D
【解析】
由条件可先求得BD的长，再根据角平分线的性质可知D到AC的距离等于BD，可得到答案．
解：∵BC=8cm，BD：CD=3：4，
∴BD=cm，
∵AD平分∠BAC，∠B=90°，
∴D到AC的距离等于BD，
∴D点到线段AC的距离为cm，
故选：D．
本题主要考查角平分线的性质，掌握角平分线上的点到角两边的距离相等是解题的关键．
20．D
【解析】
结合选项中的条件，是否能够构成的形式，若不满足全等条件即为所求；
解：由可得，判定两三角形全等已有一边和一角；
A中由可得，进而可由证明三角形全等，不符合要求；
B中，可由证明三角形全等，不符合要求；
C中由可得，进而可由证明三角形全等，不符合要求；
D中无法判定，符合要求；
故选D．
本题考查了三角形全等．解题的关键在于找出能判定三角形全等的条件．
21．C
【解析】
作DH⊥AB于D，如图，根据角平分线的性质得到DH=DC=6，然后根据三角形面积公式计算．
解：作DH⊥AB于D，如图，

∵AD平分∠BAC，DH⊥AB，DC⊥AC，
∴DH=DC=6，
∴S△ABD=×12×6=36．
故选：C．
本题考查了角平分线的性质：角的平分线上的点到角的两边的距离相等．也考查了三角形面积公式．
22．A
【解析】
根据AF=DC求出AC=DF，再根据全等三角形的判定定理逐个判断即可．
解：∵AF=DC，
∴AF+FC=DC+FC，
即AC=DF，
A、BC=EF，AC=DF，∠A=∠D，不符合全等三角形的判定定理，不能推出△ABC≌△DEF，故本选项符合题意；
B、AB=DE，∠A=∠D，AC=DF，符合全等三角形的判定定理SAS，能推出△ABC≌△DEF，故本选项不符合题意；
C．∠B=∠E，∠A=∠D，AC=DF，符合全等三角形的判定定理AAS，能推出△ABC≌△DEF，故本选项不符合题意；
D．∠ACB=∠DFE，AC=DF，∠A=∠D，符合全等三角形的判定定理ASA，能推出△ABC≌△DEF，故本选项不符合题意；
故选：A．
本题考查了全等三角形的判定定理，能熟记全等三角形的判定定理是解此题的关键，注意：全等三角形的判定定理有SAS，ASA，AAS，SSS，两直角三角形全等还有HL．
23．B
【解析】
由作法易得OD=O′D′，OC=O′C′，CD=C′D′，依据SSS可判定△COD≌△C'O'D'．
解：由作法易得OD=O′D′，OC=O′C′，CD=C′D′，
依据SSS可判定△COD≌△C'O'D'，
故选B．
本题主要考查了尺规作图—作已知角相等的角，解题的关键在于能够熟练掌握全等三角形的判定条件．
24．C
【解析】
根据全等三角形的性质：全等三角形的对应角相等，即可得到∠1=∠B，然后在三角形ABC中利用三角形内角和定理求出∠B即可得到答案．
解：如图所示，由题意得：△ABC≌△FDE，
∴∠1=∠B，
∵∠A=52°，∠C=70°，
∴∠1=∠B=180°-∠A-∠C=58°，
故选C．

本题主要考查了全等三角形的性质，三角形内角和定理，解题的关键在于能够熟练掌握全等三角形的性质．
25．B
【解析】
先证明∠CAB=∠DAE，然后根据全等三角形的判定方法对各条件进行判断．
解：∵，
∴∠CAE+∠EAB=∠DAB+∠EAB，
∴∠CAB=∠DAE，
A、添加AB=AE可利用SAS定理判定△ABC≌△AED，故此选项不符合题意；
B、添加不能判定△ABC≌△AED，故此选项符合题意；
C、添加∠C=∠D可利用ASA定理判定△ABC≌△AED，故此选项不符合题意；
D、添加∠B=∠E可利用AAS定理判定△ABC≌△AED，故此选项不符合题意；
故选B．
判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．解题关键是掌握判定两个三角形全等的方法．
26．D
【解析】
根据全等三角形的性质即可求出答案．
解：由于两个三角形全等，
∴∠1＝180﹣50°﹣72°
＝58°，
故选D．
本题考查了全等三角形的性质，属于基础题型．解答本题的关键是熟练运用全等三角形的性质
27．B
【解析】
试题解析：∵△ABE≌△ACD，
∴AB=AC，AD=AE，∠B=∠C，故A正确；
∴AB-AD=AC-AE，即BD=EC，故D正确；
在△BDF和△CEF中

∴△BDF≌△CEF（ASA），
∴DF=EF，故C正确；
故选B．
28．A
【解析】
三角形全等的判定定理有：SSS，SAS，ASA，AAS．做题时要从已知入手由易到难，不重不漏．
解：∵CD⊥AB，BE⊥AC，
∴∠ADO＝∠AEO＝90°；
∵∠1＝∠2，AO＝AO，
∴△ADO≌△AEO（AAS）．
∴AD＝AE，
∵∠DAC＝∠EAB，∠ADO＝∠AEO，
∴△ADC≌△AEB（ASA）．
∴AB＝AC，
∵∠1＝∠2，AO＝AO，
∴△AOB≌△AOC（SAS）．
∴∠B＝∠C，
∵AD＝AE，AB＝AC，
∴DB＝EC；
∵∠BOD＝∠COE，
∴△BOD≌△COE（AAS）．
故选：A．
本题考查了全等三角形的判定和性质，掌握全等三角形的判定方法（即SSS、SAS、ASA、AAS和HL）和全等三角形的性质（即全等三角形的对应边相等、对应角相等）是解题的关键．
29．C
【解析】
根据全等三角形的性质：对应角和对应边相等解答即可．
解：∵△ABC≌△ADE，
∴∠B=∠ADE=60°，AB=AD，
∴∠ADB=∠B=60°，
∴∠EDC=60°．
故选：C．
本题考查了全等三角形的性质，熟记性质并准确识图是解题的关键．
30．D
【解析】
在中，和的平分线相交于点O，根据角平分线的定义与三角形内角和定理，即可求得②正确；由平行线的性质和角平分线的定义得出和是等腰三角形得出故①正确；由角平分线的性质得出点O到各边的距离相等，故③正确；由角平分线定理与三角形面积的求解方法，即可求得③设，，则，故④正确．
解：∵在中，和的平分线相交于点O，
∴，，，
∴，
∴；故②正确；
∵在中，和的平分线相交于点O，
∴，．
∵EF∥BC，
∴，，
∴，，
∴，，
∴，故①正确；
如图：过点O作于M，作于N，连接OA，

∵在中，和的平分线相交于点O，
∴，
∴；故④正确；
∵在中，和的平分线相交于点O，
∴点O到各边的距离相等，故③正确．
故选：D．
此题考查了角平分线的定义与性质，等腰三角形的判定与性质，解题的关键是掌握角平分线及等腰三角形的性质并且注意数形结合思想的应用．
31．B
【解析】
根据垂线段最短得出当DP⊥BC时，DP的长度最小，求出∠ABD＝∠CBD，根据角平分线的性质得出AD＝DP＝6，即可得出选项．
解：∵BD⊥CD，
∴∠BDC＝90°，
∴∠C+∠CBD＝90°，
∵∠A＝90°
∴∠ABD+∠ADB＝90°，
∵∠ADB＝∠C，
∴∠ABD＝∠CBD，
当DP⊥BC时，DP的长度最小，
∵AD⊥AB，
∴DP＝AD，
∵AD＝6，
∴DP的最小值是6，
故选：B．
本题主要考查了垂线段最短和角平分线的性质，准确计算是解题的关键．
32．D
【解析】
根据角平分线上的点到角的两边距离相等可得PA=PB，再利用“AAS”证明△AOP和△BOP全等，根据全等三角形对应角相等可得∠AOP=∠BOP，全等三角形对应边相等可得OA=OB．
解：∵OP平分∠AOB，PA⊥OA，PB⊥OB，
∴PA=PB，故A选项正确；
∵∠PAO=∠PBO=90°，∠POA=∠POB，OP=OP，
∴△AOP≌△BOP（AAS），
∴∠APO=∠BPO，OA=OB，故B，C选项正确；
∵OA=OB，
∴∠OBA=∠OAB，
由等腰三角形三线合一的性质，OP垂直平分AB，AB不一定垂直平分OP，故D选项错误；
即不一定成立的是选项D，
故选：D．
本题考查了角平分线上的点到角的两边距离相等的性质，全等三角形的判定与性质，熟记性质并求出两三角形全等是解题的关键．
33．C
【解析】
根据全等三角形的判定方法一一判断即可；
A、根据ASA，可以推出△ABC≌△DEF，本选项不符合题意．
B、根据AAS，可以推出△ABC≌△DEF，本选项不符合题意．
C、SSA，不能判定三角形全等，本选项符合题意．
D、根据SAS，可以推出△ABC≌△DEF，本选项不符合题意．
故选：C．
本题考查了全等三角形的判定，解题的关键是熟练掌握全等三角形的判定方法；
34．D
【解析】
根据全等三角形的判定，利用ASA、SAS、AAS即可得答案．
解：∵AC=DF，AB=DE，
∴添加∠A=∠D，可利用SAS证明△ABC≌△DEF，故A不符合题意；
∴添加BE=CF，得出BC=EF，利用SSS证明△ABC≌△DEF，故B不符合题意；
∴添加∠ACB=∠DFE=90°，利用HL证明Rt△ABC≌Rt△DEF，故C不符合题意；
添加∠B=∠DEF，不能证明△ABC≌△DEF，故D符合题意；
故选：D．
本题考查了全等三角形的判定，掌握全等三角形的判定方法：SSS、ASA、SAS、AAS和HL是解题的关键．
35．C
【解析】
甲不符合三角形全等的判断方法，乙可运用SAS判定全等，丙可运用AAS证明两个三角形全等．
由图形可知，甲有两边一角，但50°的角不是两边的夹角，故不能判断两三角形全等，乙有两边及其夹角，能判断两三角形全等，丙得出两角及其一角对边，能判断两三角形全等，根据全等三角形的判定得：乙丙正确．
故选C．
本题考查了三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．
注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．
36．A
【解析】
根据题意可得，对顶角相等即，再根据全等三角形的判定定理（SAS，ASA，AAS，SSS）逐个判断即可．
A．，它们的夹角是，不是，
∴无法判定≌，故本选项符合.
B．在≌中，
，
∴≌(ASA)，故本选项不符合.
C．在≌中，
，
∴≌(AAS)，故本选项不符合.
D．,
,
在≌中，
，
∴≌(SAS)，故本选项不符合.
故选A.
此题考查全等三角形的判定，解题关键在于掌握全等三角形的判定定理（SAS，ASA，AAS，SSS）.
37．C
【解析】
由条件可证△AOD≌△BOC，可得∠A=∠B，则可证明△ACE≌△BDE，可得AE=BE，则可证明△AOE≌△BOE，可得∠COE=∠DOE，可证△COE≌△DOE，可求得答案．
解：

在△AOD和△BOC中
∴△AOD≌△BOC（SAS），
∴∠A=∠B，
∵OC=OD，OA=OB，
∴AC=BD，
在△ACE和△BDE中
∴△ACE≌△BDE（AAS），
∴AE=BE，
在△AOE和△BOE中
∴△AOE≌△BOE（SAS），
∴∠COE=∠DOE，
在△COE和△DOE中
∴△COE≌△DOE（SAS），
故全等的三角形有4对，
故选C．
本题主要考查全等三角形的性质和判定，掌握全等三角形的判定方法是解题的关键，即SSS、SAS、ASA、AAS和HL．
38．C
【解析】
根据全等三角形的判定方法或者举出反例能证明原命题是错误的，分别判断各命题的正误即可．
①一条直角边和斜边上的高对应相等的两个直角三角形全等；根据HL可证得两直角三角形全等，此命题正确；
②有两条边相等的两个直角三角形不一定全等；比如一直角三角形的两直角边和另一个直角三角形的一直角边和一斜边相等，则这两个直角三角形并不全等；原命题错误；
③有一边相等的两个等边三角形全等，符合SSS定理，此命题正确；
④两边和其中一边的对角对应相等的两个三角形不一定全等，根据SSA并不能证明三角形全等；故原命题错误；
故选C．
本题考查了全等三角形的判定的应用，能理解全等三角形的判定定理是解此题的关键，普通两个三角形全等共有四个定理，即AAS、ASA、SAS、SSS，直角三角形可用HL定理，但AAA、SSA，无法证明三角形全等．
39．A
【解析】
过两把直尺的交点C作CF⊥BO与点F，由题意得CE⊥AO，因为是两把完全相同的长方形直尺，可得CE=CF，再根据角的内部到角的两边的距离相等的点在这个角的平分线上可得OP平分∠AOB
如图所示：过两把直尺的交点C作CF⊥BO与点F，由题意得CE⊥AO，

∵两把完全相同的长方形直尺，
∴CE=CF，
∴OP平分∠AOB（角的内部到角的两边的距离相等的点在这个角的平分线上），
故选A．
本题主要考查了基本作图，关键是掌握角的内部到角的两边的距离相等的点在这个角的平分线上这一判定定理．
40．B
【解析】
作于，根据角平分线的性质得到，根据三角形的面积公式计算即可．
解：作于，

由基本作图可知，平分
平分，，，
，
的面积，
故选：B．
本题考查基本作图、角平分线的性质定理、三角形的面积等知识，解题的关键是灵活运用所学知识解决问题．
41．C
【解析】
解：①∵AD是△ABC的中线，
∴BD=CD，
∴△ABD和△ACD面积相等；故①正确；
②若在△ABC中，当AB≠AC时，AD不是∠BAC的平分线，即∠BAD≠∠CAD．即②不一定正确；
③∵AD是△ABC的中线，
∴BD=CD，
在△BDF和△CDE中，
∵BD=CD，∠BDF=∠CDE，DF=DE，
∴△BDF≌△CDE（SAS）．故③正确；
④∵△BDF≌△CDE，
∴∠CED=∠BFD，
∴BF∥CE；故④正确；
⑤∵△BDF≌△CDE，
∴CE=BF，
∴只有当AE=BF时，CE=AE．故⑤不一定正确．
综上所述，正确的结论是：①③④，共有3个．
故选C．

42．B
【解析】
由△ABC≌△DCB，A、B的对应顶点分别为点D、C，根据全等三角形的对应边相等，即可得BD=CA，又由AC=9cm，即可求得BD的长．
解：∵△ABC≌△DCB，A、B的对应顶点分别为点D、C，
∴BD=CA，
∵AC=9cm，
∴BD=9cm．
故选B．
此题考查了全等三角形的性质．此题比较简单，解题的关键是注意掌握全等三角形的对应边相等，注意对应关系．
43．C
【解析】
①证明△BAD≌△CAE,再利用全等三角形的性质即可判断；②由△BAD≌△CAE可得∠ABF=∠ACF，再由∠ABF+∠BGA=90°、∠BGA=∠CGF证得∠BFC=90°即可判定；③分别过A作AM⊥BD、AN⊥CE,根据全等三角形面积相等和BD=CE，证得AM=AN,即AF平分∠BFE,即可判定；④由AF平分∠BFE结合即可判定．
解：∵∠BAC=∠EAD
∴∠BAC+∠CAD=∠EAD+∠CAD,即∠BAD=∠CAE
在△BAD和△CAE中
AB=AC, ∠BAD=∠CAE,AD=AE
∴△BAD≌△CAE
∴BD=CE
故①正确；
∵△BAD≌△CAE
∴∠ABF=∠ACF
∵∠ABF+∠BGA=90°、∠BGA=∠CGF
∴∠ACF+∠BGA=90°,
∴∠BFC=90°
故②正确；

分别过A作AM⊥BD、AN⊥CE垂足分别为M、N
∵△BAD≌△CAE
∴S△BAD=S△CAE,
∴
∵BD=CE
∴AM=AN
∴平分∠BFE，无法证明AF平分∠CAD．
故③错误；

∵平分∠BFE，
∴
故④正确．
故答案为C．
本题考查了全等三角形的判定与性质、角平分线的判定与性质以及角的和差等知识，其中正确应用角平分线定理是解答本题的关键．