北师大版九年级上册第二章 一元二次方程2 用配方法求解一元二次方程精品课件ppt

这是一份北师大版九年级上册第二章 一元二次方程2 用配方法求解一元二次方程精品课件ppt，文件包含221《用配方法解简单一元二次方程的解》课件PPTpptx、221《用配方法求解简单一元二次方程》教案docx等2份课件配套教学资源，其中PPT共16页， 欢迎下载使用。

填一填：1.如果 x2 = a,那么 x=.4.完全平方式:式子a2 ± 2ab +b2叫完全平方式,且a2 ± 2ab +b2 =.
2.如果 x2=64 ,则x= .
3.任何数都可以作为被开方数吗？
负数不可以作为被开方数.
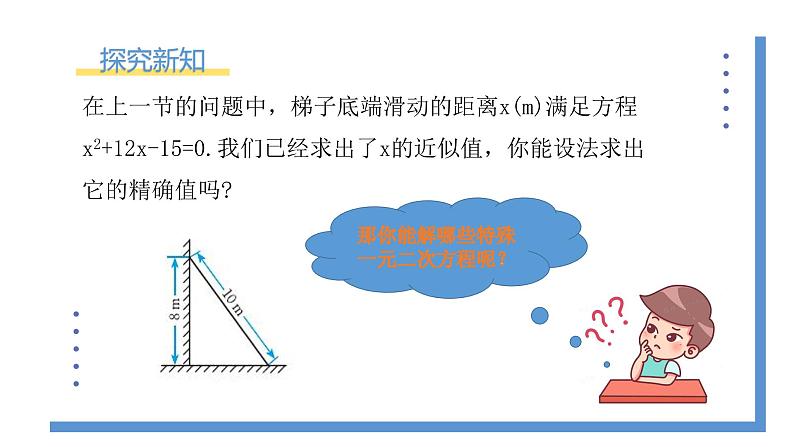
在上一节的问题中，梯子底端滑动的距离x(m)满足方程x2+12x-15=0.我们已经求出了x的近似值，你能设法求出它的精确值吗?
那你能解哪些特殊一元二次方程呢？
你会解下列一元二次方程吗？你是怎么做的？
x2=52x2+3=5x2+2x+1=5(x+6)2+72=102
方程可化为x2=1，所以x1=1 , x2=-1.
观察下面的一元二次方程，它们都有什么特点？
等号一边是平方或者是可以化为完全平方式的形式，另一边是一个非负常数的形式.
对于这种类型的一元二次方程可以利用平方根的定义直接开平方求一元二次方程的根的方法叫直接开平方法.
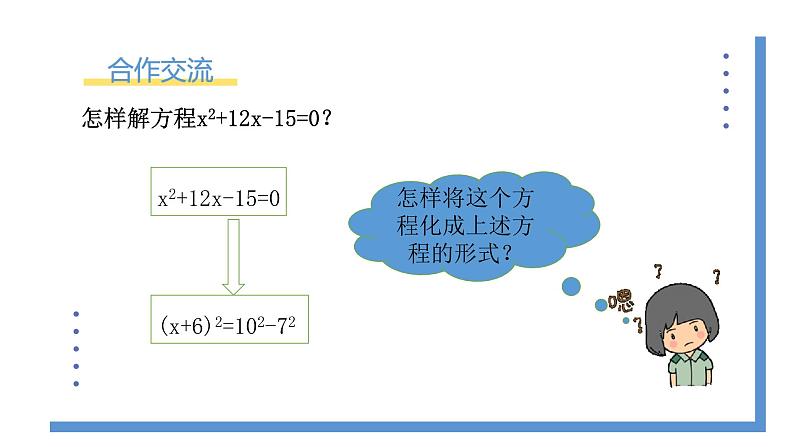
怎样解方程x2+12x-15=0？
怎样将这个方程化成上述方程的形式？
x2+12x-15=0
(x+6)2=102-72
填一填：（1）x2 +12x + _____ = ( x + 6 )2　;（2）x2 - 4x + _____ = ( x - ____ )2　;（3）x2 + 8 x + ____ = ( x + ____ )2 .
问题：上面等式的左边常数项和一次项系数有什么关系？对于形如 x2 + ax的式子，如何配成完全平方？
x2 + ax + ( )2 = ( x + )2
等式左边常数项是一次项系数的一半的平方.
将一次项12x改写成2·x·6，得x2+2·x·6=15
为使左边成为完全平方式，只需在方程两边都加上62
即：x2+2·x·6+62=15+62， （x+6）2=51
两边开平方，得x+6=
配方法：通过配成完全平方式的方法得到了一元二次方程的根，这种解一元二次方程的方法称为配方法.用配方法解形如 x2 + px + q = 0①将常数项移到方程的右边. x2 + px = -q②两边都加上一次项系数一半的平方. x2 + px + （ ）2 = （ ）2 - q③直接用开平方法求出它的解. （x + ）2 = （ ）2 - q
【例1】解方程x2+8x－9=0
解：移项，得x2+8x=9，
配方，得x2+8x+16=9+16，即 (x+4)2=25.
两边开平方，得x+4=±5，即 x+4=5 或 x+4=－5.∴x1=1，x2=－9.
配方的目的是什么？配方的关键是什么？配方时应注意什么？
目的：通过配成(x＋m)2＝n(n≥0)，再开方，通过降次来解方程；关键：加上一次项系数一半的平方；注意：对二次项系数为1的一元二次方程配方时要注意在方程两边都加上一次项系数一半的平方.
1.方程 x2 - 4 = 0 的解是（ ） A. x =2 B. x = -2 C. x =±2 D. x =±42.用配方法解关于x的一元二次方程 x2 - 2x - 3 = 0,配方后的方程可以是（ ）A. (x - 1) 2 = 4 B. (x + 1) 2 = 4C. (x - 1) 2 = 16 D. (x + 1) 2 = 16
(1)方程x2=0.25的根是 . (2)方程2x2=18的根是 . (3)方程(2x-1)2=9的根是 .
4. 解下列方程： (1)x2-81＝0； (2)2x2＝50； (3)(x＋1)2=4 .
x1=0.5,x2=-0.5
解：x1＝9, x2＝－9；
解：x1＝5, x2＝－5；
解：x1＝1, x2＝－3.
5. 解方程：x2 + 2x + 5 = 8解：移项，得 x2 + 2x = 3,配方，得 x2 + 2x + 1 = 3 + 1 ,即（x + 1）2 = 4.开平方, 得 x + 1 = ±2.解得x1 = 1 , x2= -3.
配方法解二次项系数为1的一元二次方程的基本步骤：
(1)移项：把常数项移到方程的右边；(2)配方：方程两边同时加上一次项系数一半的平方；(3)开方：根据平方根的意义,方程两边开平方;(4)求解：解一元一次方程;(5)定解：写出原方程的解.