华师大版九年级上册22.1 一元二次方程公开课教案及反思

这是一份华师大版九年级上册22.1 一元二次方程公开课教案及反思，共5页。教案主要包含了江苏淮安中考，辽宁锦州中考等内容，欢迎下载使用。
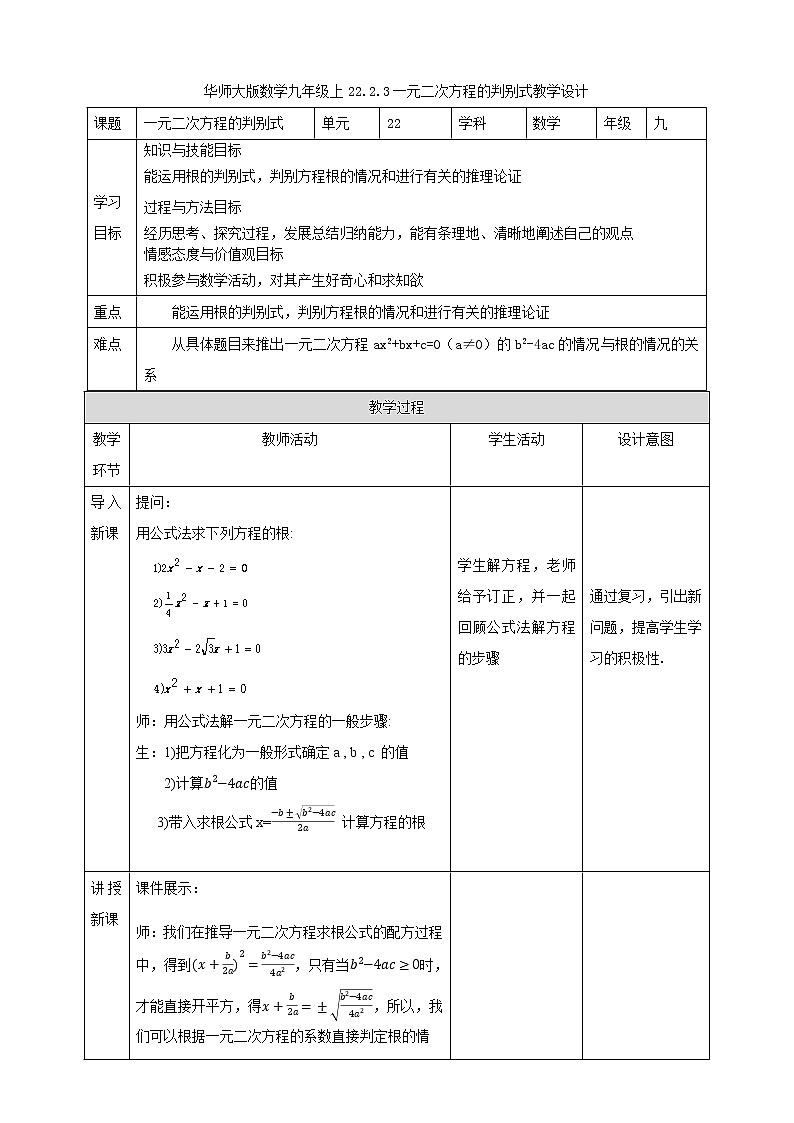
华师大版数学九年级上22.2.3一元二次方程的判别式教学设计课题 一元二次方程的判别式单元22学科数学年级九学习目标知识与技能目标能运用根的判别式，判别方程根的情况和进行有关的推理论证过程与方法目标经历思考、探究过程，发展总结归纳能力，能有条理地、清晰地阐述自己的观点情感态度与价值观目标积极参与数学活动，对其产生好奇心和求知欲重点能运用根的判别式，判别方程根的情况和进行有关的推理论证难点从具体题目来推出一元二次方程ax2+bx+c=0（a≠0）的b2-4ac的情况与根的情况的关系 教学过程教学环节教师活动学生活动设计意图导入新课提问：用公式法求下列方程的根:     师：用公式法解一元二次方程的一般步骤:生：1)把方程化为一般形式确定a , b , c 的值2)计算的值3)带入求根公式x= 计算方程的根   学生解方程，老师给予订正，并一起回顾公式法解方程的步骤     通过复习，引出新问题，提高学生学习的积极性.讲授新课课件展示：师：我们在推导一元二次方程求根公式的配方过程中，得到，只有当时，才能直接开平方，得，所以，我们可以根据一元二次方程的系数直接判定根的情况.师：观察方程，我们发现有几种情况？生：有三种师：有哪三种呢？生：当时，方程的右边是一个正数，方程有两个不相等的实数根：生：当b2-4ac=0时，方程的右边是0，方程有两个相等的实数根：生：当b2-4ac<0时，方程的右边是一个负数，因为在实数范围内，负数没有平方根，所以，方程没有实数根师：思考：究竟是谁决定了一元二次方程根的情况生：师：一元二次方程ax2＋bx＋c＝0(a≠0)的根的判别式为b2－4ac，通常用符号“Δ”来表示.那么总结一下Δ与根的关系吧生： (1)当 Δ＝b2－4ac＞0时，一元二次方程有两个不相等的实数根.(2)当 Δ＝b2－4ac＝0时，一元二次方程有两个相等的实数根.(3)当 Δ＝b2－4ac＜0时，一元二次方程无实数根. 师：反过来，对于方程上面的结论能成立吗？生：能成立的(1)若方程ax2＋bx＋c＝0(a≠0)有两个不相等的实数根，则Δ＝b2－4ac>0.(2)若方程ax2＋bx＋c＝0(a≠0)有两个相等的实数根，则Δ＝b2－4ac＝0.(3)若方程ax2＋bx＋c＝0(a≠0)没有实数根，则Δ＝b2－4ac<0.课件展示：例1、不解方程，判断下列方程的根的情况： (1)       (2)        (3)4                         师：总结一下一般步骤：生：(1)化为一般式，确定 a，b，c的值.  (2) 计算Δ的值，确定Δ的符号.  (3)判别根的情况，得出结论课件展示试一试已知关于x的方程                          (1)当k取何值时，方程有两个不相等的实数根？(2)当k取何值时，方程有两个相等的实数根？(3)当k取何值时，方程没有实数根？             学生配方，推导求根公式，讨论得出求根公式的三种情况，并总结出决定了根的情况            师生总结Δ与根的关系        学生解答，老师订正       学生自主解答            学生通过自己解决问题，充分发挥学习的主动性，同时也培养了学生归纳问题的能力。             巩固所学知识，培养学生分析归纳的能力.       培养学生发散思维，自己解决问题的能力      课堂练习1、下列方程有两个相等的实数根的是(　　)   A．x2＋x＋1＝0        B．4x2＋2x＋1＝0   C．x2＋12x＋36＝0        D．x2＋x－2＝0答案：C2、若关于x的一元二次方程(k－1)x2＋4x＋1＝0有两个不相等的实数根，则k的取值范围是(　　)  A．k＜5　               B．k＜5且k≠1  C．k≤5且k≠1　       D．k＞5 答案：B3.已知关于x的一元二次方程x－k＝0有两个相等的实数根，则k的值为_______.答案：-34．若关于x的方程k－4x－＝0有实数根，则k的取值范围是__________. 答案： k≥-65．关于x的一元二次方程x2＋(2m＋1)x＋m2－1＝0有两个不相等的实数根.(1)求m的取值范围；(2)写出一个满足条件的m的值，并求此时方程的根.答案：解：(1)∵关于x的一元二次方程x2＋(2m＋1)x＋m2－1＝0有两个不相等的实数根，∴Δ＝(2m＋1)2－4×1×(m2－1)＝4m＋5＞0，解得m＞.故m的取值范围是m>-.(2)当m＝1时，原方程为x2＋3x＝0，即x(x＋3)＝0，解得x1＝0，∴x2＝－3. 拓展提高已知关于x的一元二次方程 mx2－(m＋2)x＋2＝0.(1)证明：不论m为何值时，方程总有实数根；(2)m为何整数时，方程有两个不相等的正整数根. 答案：(1)证明：Δ＝(m＋2)2－8m＝m2－4m＋4＝(m－2)2.∵不论m为何值时，(m－2)2≥0，∴Δ≥0，∴方程总有实数根.(2)解：解方程，得x＝，∴x1＝，x2＝1.∵方程有两个不相等的正整数根，且m为整数，∴m＝1或m＝2(不合题意，舍去)，∴m＝1. 中考链接1. 【江苏淮安中考】若关于x的一元二次方程x2－2x－k＋1＝0有两个相等的实数根，则k的值是              (　　)A．－1　B．0　C．1　 D．2答案：B2.【辽宁锦州中考】一元二次方程2x2－x＋1＝0的根的情况是 (　　)A．有两个不相等的实数根　 B．有两个相等的实数根C．没有实数根　           D．无法判断 答案：C            学生自主解答，教师讲解答案。                      学生自主解答，教师讲解答案。            练中考题型       通过这几道题目来反馈学生对本节所学知识的掌握程度，落实基础。学生刚刚接触到新的知识需要一个过程，也就是对新知识从不熟悉到熟练的过程，无论是基础的习题，还是变式强化，都要以学生理解透彻为最终目标。               可以照顾不层次的学生，调动学生学习积极性          让学生更早的接触中考题型，熟悉考点.课堂小结学生归纳本节所学知识回顾学过的知识，总结本节内容，提高学生的归纳以及语言表达能力。板书1.一元二次方程根的判别式一元二次方程ax2＋bx＋c＝0(a≠0)的根的判别式为b2－4ac，通常用符号“Δ”来表示.2.判别式与根的情况(1)当 Δ＝b2－4ac＞0时，一元二次方程有两个不相等的实数根.(2)当 Δ＝b2－4ac＝0时，一元二次方程有两个相等的实数根.(3)当 Δ＝b2－4ac＜0时，一元二次方程无实数根.