高考物理二轮复习第1章运动的描述匀变速直线运动微专题1运动图象和追及相遇问题学案

这是一份高考物理二轮复习第1章运动的描述匀变速直线运动微专题1运动图象和追及相遇问题学案，共9页。

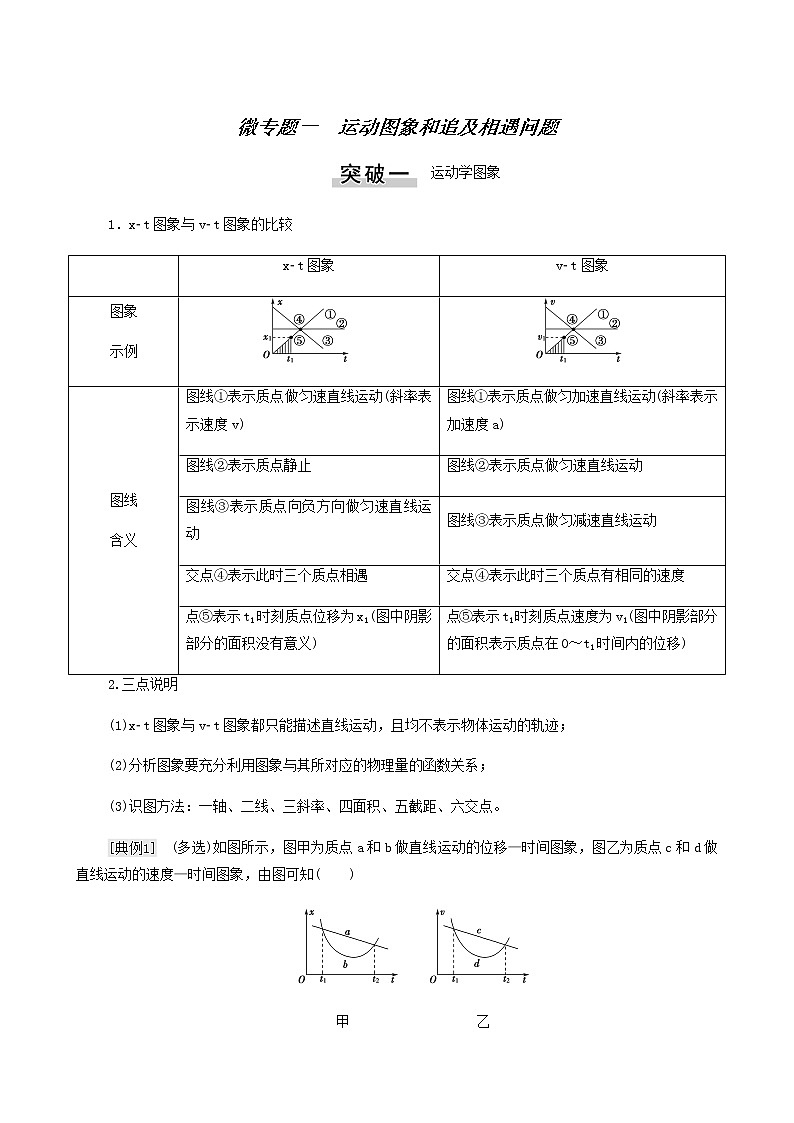
1．x­t图象与v­t图象的比较
2.三点说明
(1)x­t图象与v­t图象都只能描述直线运动，且均不表示物体运动的轨迹；
(2)分析图象要充分利用图象与其所对应的物理量的函数关系；
(3)识图方法：一轴、二线、三斜率、四面积、五截距、六交点。
eq \([典例1]) (多选)如图所示，图甲为质点a和b做直线运动的位移—时间图象，图乙为质点c和d做直线运动的速度—时间图象，由图可知( )
甲 乙
A．若t1时刻a、b两质点第一次相遇，则t2时刻两质点第二次相遇
B．若t1时刻c、d两质点第一次相遇，则t2时刻两质点第二次相遇
C．t1到t2时间内，四个质点中只有b和d两个质点的运动方向发生改变
D．t1到t2时间内，四个质点中只有b和d两个质点的速率先减小后增大
思路点拨：解此题关键有两点：
(1)明确图象所反映的运动规律。
(2)区分两类图象中“交点”“斜率”“截距”的物理意义。
AD [在位移—时间图象中，两图线的交点表示两质点在同一时刻位置相同而相遇，由甲图可知，若t1时刻a、b两质点第一次相遇，则t2时刻两质点第二次相遇，故A正确；t1到t2时间内，根据v­t图象的“面积”表示位移知c的位移大于d的位移，若t1时刻c、d两质点第一次相遇，则t2时刻两质点不能相遇，故B错误；只有b运动方向改变，a、c、d质点的运动方向未发生改变，故C错误；根据x­t图象的斜率表示速度，知t1到t2时间内，a质点的速率不变，b质点的速率先减小后增大，由v­t图象知，c的速率均匀减小，d的速率先减小后增大，故D正确。]
“三步”巧解图象问题
eq \([跟进训练])
x­t图象的应用
1.(2020·湖北重点中学联考)在平直公路上行驶的a车和b车，其位移—时间(x­t)图象分别为图中直线a和曲线b，已知b车的加速度恒定且等于－2 m/s2，t＝3 s时，直线a和曲线b刚好相切，则( )
A．a车做匀速直线运动且其速度为va＝eq \f(8,3) m/s
B．t＝3 s时a车和b车相遇但此时速度不等
C．t＝1 s时b车的速度为10 m/s
D．t＝0时a车和b车的距离x0＝9 m
D [由图知，a车做匀速直线运动，其速度为va＝eq \f(8 m－2 m,3 s)＝2 m/s，A错误；由图知，t＝3 s时，a、b两车相遇，x­t图象中图线切线的斜率表示速度，由于直线a与曲线b相切，故两车的速度相等，B错误；1～3 s内，由匀变速直线运动规律得，v3＝v1＋at，解得v1＝v3－at＝2 m/s－(－2 m/s2)×2 s＝6 m/s，C错误；t＝0时，a车位置xa0＝2 m，b车在第1 s内的位移x＝v1t＋eq \f(1,2)·(－a)·t2＝7 m，由图知，x＝x1－xb0，解得b车在t＝0时的位置为xb0＝－7 m，故此时两车的距离x0＝9 m，D正确。]
v­t图象的应用
2.(2020·安徽安庆示范中学高三联考)甲、乙两车并排停在斑马线处礼让行人，在行人经过斑马线后，甲、乙两车同时启动并沿平直公路同向行驶，其速度—时间图象分别为图中直线a和曲线b，由图可知( )
A．t0时刻两车并排行驶
B．t0时刻乙车的运动方向发生改变
C．在0～t0时间内，乙车的加速度越来越小
D．在0～t0时间内，乙车的平均速度为eq \f(v0,2)
C [根据v­t图象与时间轴所围成的面积表示位移，知在0～t0时间内，乙车的位移比甲车的大，则t0时刻乙车在甲车的前方，故A错误；乙车的速度一直为正，运动方向没有改变，故B错误；在0～t0时间内，乙车图象切线斜率越来越小，则乙车的加速度越来越小，故C正确；在0～t0时间内，甲车做匀加速直线运动，平均速度为eq \f(v0,2)，乙车的位移比甲车的大，则乙车的平均速度大于甲车的平均速度，即大于eq \f(v0,2)，故D错误。]
非常规图象的分析及应用
3．(2020·福建三明市质量检测)如图所示四幅图为物体做直线运动的图象，下列说法正确的是( )
甲 乙
丙 丁
A．甲图中，物体在0～t0这段时间内的位移小于eq \f(v0t0,2)
B．乙图中，物体的加速度为2 m/s2
C．丙图中，阴影面积表示t1～t2时间内物体的加速度变化量
D．丁图中，t＝3 s时物体的速度为25 m/s
D [题图甲中，因v­t图象与t轴围成的面积等于位移，可知物体在0～t0这段时间内的位移大于eq \f(v0t0,2)，选项A错误；题图乙中，根据v2＝2ax可知2a＝eq \f(15,15) m/s2＝1 m/s2，则物体的加速度为0.5 m/s2，选项B错误；题图丙中，根据Δv＝aΔt可知，阴影面积表示t1～t2时间内物体的速度变化量，选项C错误；题图丁中，由x＝v0t＋eq \f(1,2)at2可得eq \f(x,t)＝v0＋eq \f(1,2)at，由图象可知eq \f(1,2)a＝eq \f(10,2) m/s2＝5 m/s2，则v0＝－5 m/s，a＝10 m/s2；则t＝3 s时物体的速度为v3＝v0＋at3＝25 m/s，选项D正确。]
追及相遇问题
1．解答追及和相遇问题的三种方法
2.情景分析法的基本思路
eq \([典例2]) (一题多解)在水平轨道上有两列火车A和B相距s，A车在后面做初速度为v0、加速度大小为2a的匀减速直线运动，而B车同时做初速度为零、加速度为a的匀加速直线运动，两车运动方向相同。要使两车不相撞，求A车的初速度v0满足什么条件。
思路点拨：要使两车恰好不相撞，A车追上B车时其速度只能与B车相等。设A、B两车从相距s到A车追上B车时，A车的位移为sA、末速度为vA、所用时间为t，B车的位移为sB、末速度为vB，两者的运动过程如图所示。
[解析] 法一：临界法
利用位移公式、速度公式求解
对A车有sA＝v0t＋eq \f(1,2)×(－2a)×t2
vA＝v0＋(－2a)×t
对B车有sB＝eq \f(1,2)at2，vB＝at
对两车有s＝sA－sB
追上时，两车不相撞的临界条件是vA＝vB
联立以上各式解得v0＝eq \r(6as)
故要使两车不相撞，A车的初速度v0应满足的条件是
v0法二：函数法
利用判别式求解，由法一可知sA＝s＋sB
即v0t＋eq \f(1,2)×(－2a)×t2＝s＋eq \f(1,2)at2
整理得3at2－2v0t＋2s＝0
这是一个关于时间t的一元二次方程，当根的判别式Δ＝(－2v0)2－4×3a×2s<0时，t无实数解，即两车不相撞，所以要使两车不相撞，A车的初速度v0应满足的条件是v0法三：图象法
利用速度—时间图象求解，先作A、B两车的速度—时间图象，其图象如图所示，设经过t′时间两车刚好不相撞，则对A车有vA＝v′＝v0－2at′
对B车有vB＝v′＝at′
以上两式联立解得t′＝eq \f(v0,3a)
经t′时间两车发生的位移大小之差，即原来两车间的距离s，它可用图中的阴影面积表示，由图象可知s＝eq \f(1,2)v0·t′＝eq \f(1,2)v0·eq \f(v0,3a)＝eq \f(v\\al(2,0),6a)，所以要使两车不相撞，A车的初速度v0应满足的条件是v0[答案] v0 求解“追及、相遇”问题的思路和技巧
(1)解题思路

(2)解题技巧
①紧抓“一图三式”，即：过程示意图，时间关系式、速度关系式和位移关系式。
②审题应抓住题目中的关键字眼，充分挖掘题目中的隐含条件，如“刚好”“恰好”“最多”“至少”等，它们往往对应一个临界状态，满足相应的临界条件。
eq \([跟进训练])
常见追及相遇问题
1．汽车A以vA＝4 m/s的速度向右做匀速直线运动，发现前方相距x0＝7 m处、以vB＝10 m/s的速度同向运动的汽车B正开始匀减速刹车直到静止后保持不动，其刹车的加速度大小a＝2 m/s2。从此刻开始计时。求：
(1)A追上B前，A、B间的最远距离是多少？
(2)经过多长时间A恰好追上B?
[解析] (1)当A、B两汽车速度相等时，两车间的距离最远，即v＝vB－at＝vA，解得t＝3 s①
此时汽车A的位移xA＝vAt＝12 m②
汽车B的位移xB＝vBt－eq \f(1,2)at2＝21 m③
故最远距离Δxmax＝xB＋x0－xA＝16 m。④
(2)汽车B从开始减速直到静止经历的时间
t1＝eq \f(vB,a)＝5 s⑤
运动的位移x′B＝eq \f(v\\al(2,B),2a)＝25 m⑥
汽车A在t1时间内运动的位移
x′A＝vAt1＝20 m⑦
此时相距Δx＝x′B＋x0－x′A＝12 m⑧
汽车A需再运动的时间t2＝eq \f(Δx,vA)＝3 s⑨
故A追上B所用时间t总＝t1＋t2＝8 s。⑩
[答案] (1)16 m (2)8 s
与图象结合的追及相遇问题
2.(2020·广东深圳市第一次调研)可视为质点的甲、乙两小车分别沿同一平直路面同向行驶，t＝0时，甲在乙前方16 m处，它们的v­t图象如图所示，则下列说法正确的是( )
A．甲、乙在t＝2 s和t＝10 s时刻并排行驶
B．甲、乙在t＝4 s和t＝8 s时刻并排行驶
C．在t＝6 s时刻，乙车在甲车前8 m处
D．在t＝6 s时刻，乙车在甲车前18 m处
B [由题图图象可知，甲做初速度为0、加速度为a1＝eq \f(12,6) m/s2＝2 m/s2的匀加速运动；乙做初速度为v0＝6 m/s、加速度为a2＝eq \f(12－6,6) m/s2＝1 m/s2的匀加速运动；两车相遇时满足：v0t＋eq \f(1,2)a2t2＝s0＋eq \f(1,2)a1t2，即6t＋eq \f(1,2)×1×t2＝16＋eq \f(1,2)×2t2，解得t1＝4 s，t2＝8 s，即甲、乙在t＝4 s和t＝8 s时刻并排行驶，选项A错误，B正确。在t＝6 s时，甲的位移：x1＝eq \f(1,2)×2×62 m＝36 m；乙的位移：x2＝6×6 m＋eq \f(1,2)×1×62 m＝54 m，可知此时乙在甲的前面，Δx＝x2－x1－s0＝54 m－36 m－16 m＝2 m，故选项C、D错误。]
3．具有我国自主知识产权的“歼­10”飞机的横空出世，证实了我国航空事业在飞速发展，而航空事业的发展又离不开风洞试验，其简化模型如图a所示。在光滑的水平轨道上停放相距x0＝10 m的甲、乙两车，其中乙车是风力驱动车。在弹射装置使甲车获得v0＝40 m/s的瞬时速度向乙车运动的同时，乙车的风洞开始工作，将风吹向固定在甲车上的挡风板，从而使乙车获得了速度，测绘装置得到了甲、乙两车的v­t图象如图b所示，设两车始终未相撞。
a b
(1)若甲车的质量与其加速度的乘积等于乙车的质量与其加速度的乘积，求甲、乙两车的质量比；
(2)求两车相距最近时的距离。
[解析] (1)由题图b可知：甲车加速度的大小a甲＝eq \f(40－10,t1) m/s2
乙车加速度的大小a乙＝eq \f(10－0,t1) m/s2
因甲车的质量与其加速度的乘积等于乙车的质量与其加速度的乘积，所以有：m甲a甲＝m乙a乙
解得eq \f(m甲,m乙)＝eq \f(1,3)。
(2)在t1时刻，甲、乙两车的速度相等，均为v＝10 m/s，此时两车相距最近
对乙车有：v＝a乙t1
对甲车有：v＝a甲(0.4 s－t1)
可解得t1＝0.3 s
车的位移等于v­t图线与时间轴所围的面积，有：
x甲＝eq \f(40＋10×0.3,2) m＝7.5 m，
x乙＝eq \f(10×0.3,2) m＝1.5 m
两车相距最近时的距离为
xmin＝x0＋x乙－x甲＝4 m。
[答案] (1)eq \f(1,3) (2)4 m
x­t图象
v­t图象
图象
示例
图线
含义
图线①表示质点做匀速直线运动(斜率表示速度v)
图线①表示质点做匀加速直线运动(斜率表示加速度a)
图线②表示质点静止
图线②表示质点做匀速直线运动
图线③表示质点向负方向做匀速直线运动
图线③表示质点做匀减速直线运动
交点④表示此时三个质点相遇
交点④表示此时三个质点有相同的速度
点⑤表示t1时刻质点位移为x1(图中阴影部分的面积没有意义)
点⑤表示t1时刻质点速度为v1(图中阴影部分的面积表示质点在0～t1时间内的位移)
情景
分析法
抓住“两物体能否同时到达空间某位置”这一关键，认真审题，挖掘题目中的隐含条件，建立一幅物体运动关系的情景图
函数
判断法
设相遇时间为t，根据条件列方程，得到关于位移x与时间t的函数关系，由此判断两物体追及或相遇情况
图象
分析法
将两个物体运动的速度—时间关系或位移—时间关系画在同一图象中，然后利用图象分析求解相关问题