
13.1轴对称 人教版初中数学八年级上册同步练习(含答案解析)
展开13.1轴对称人教版初中数学八年级上册同步练习
学校:___________姓名:___________班级:___________考号:___________
第I卷(选择题)
一、选择题(本大题共12小题,共36.0分)
- 如图,桌面上有、两球,若要将球射向桌面的任意一边,使一次反弹后击中球,则、、、各点中,可以瞄准的是( )
A. 点
B. 点
C. 点
D. 点
- 如图,在中,按以下步骤作图:
分别以,为圆心,大于的长为半径作弧,两弧相交于点,;
作直线交于点,交于点,连接下列说法不确定的是( )
A. B. C. D.
- 如图,在中,按以下步骤作图:分别以点,为圆心,以大于的长为半径画弧,两弧分别交于,两点;作直线,分别交,于点,,连接若,,,则的周长是( )
A. B. C. D.
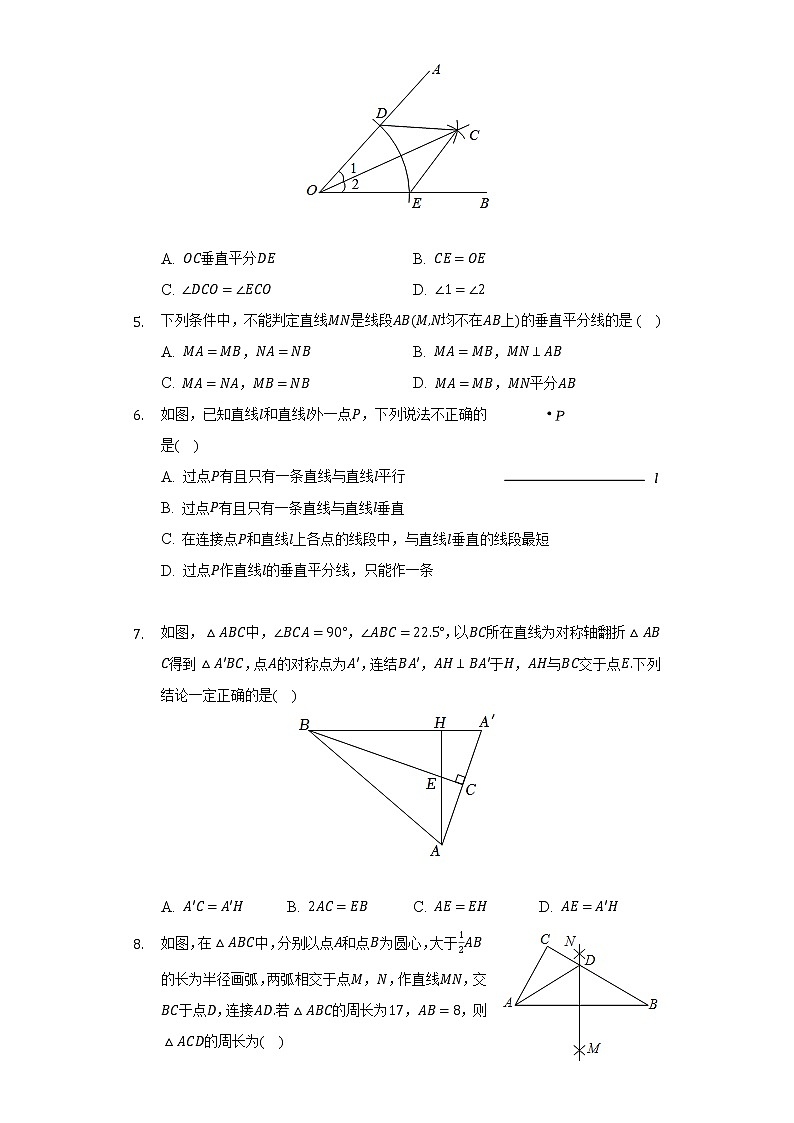
- 按以下步骤进行尺规作图:以点为圆心,任意长为半径作弧,交的两边、于、两点;分别以点、为圆心,大于的长为半径作弧,两弧交于点;作射线,并连接、下列结论不正确的是( )
A. 垂直平分 B.
C. D.
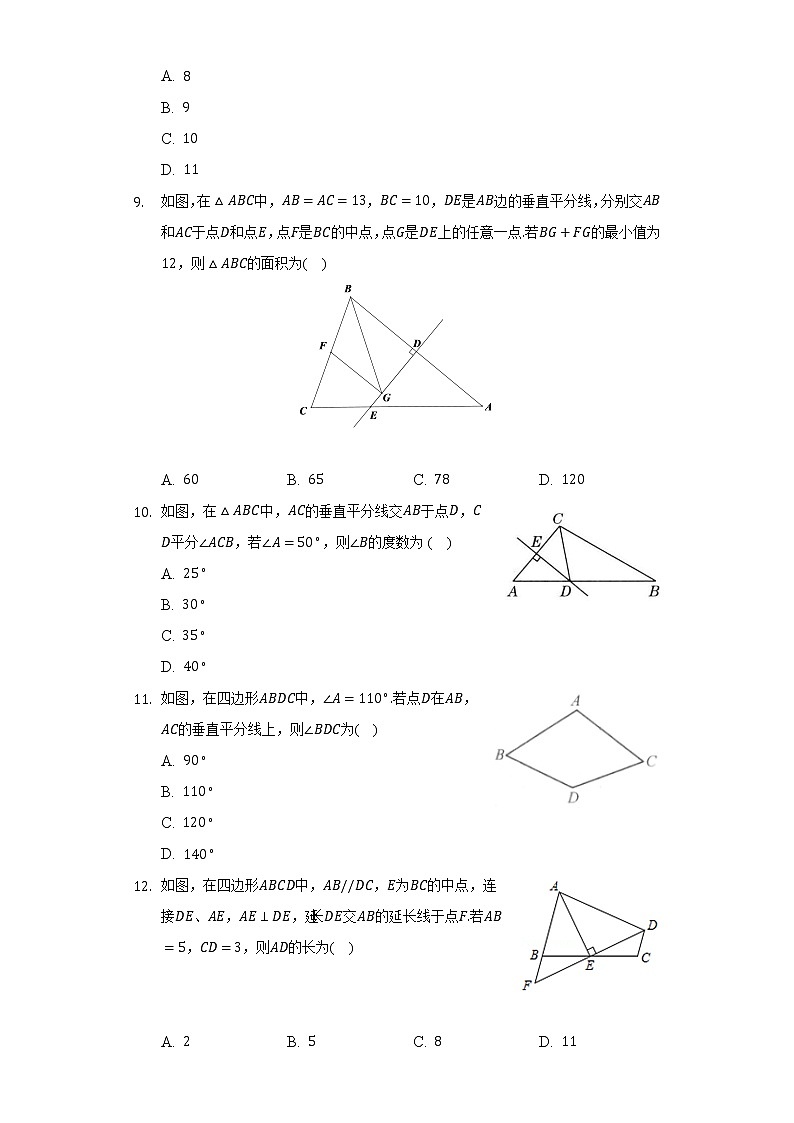
- 下列条件中,不能判定直线是线段均不在上的垂直平分线的是( )
A. , B. ,
C. , D. ,平分
- 如图,已知直线和直线外一点,下列说法不正确的是( )
A. 过点有且只有一条直线与直线平行
B. 过点有且只有一条直线与直线垂直
C. 在连接点和直线上各点的线段中,与直线垂直的线段最短
D. 过点作直线的垂直平分线,只能作一条
- 如图,中,,,以所在直线为对称轴翻折得到,点的对称点为,连结,于,与交于点下列结论一定正确的是( )
A. B. C. D.
- 如图,在中,分别以点和点为圆心,大于的长为半径画弧,两弧相交于点,,作直线,交于点,连接若的周长为,,则的周长为( )
A.
B.
C.
D.
- 如图,在中,,,是边的垂直平分线,分别交和于点和点,点是的中点,点是上的任意一点若的最小值为,则的面积为( )
A. B. C. D.
- 如图,在中,的垂直平分线交于点,平分,若,则的度数为( )
A.
B.
C.
D.
- 如图,在四边形中,若点在,的垂直平分线上,则为( )
A.
B.
C.
D.
- 如图,在四边形中,,为的中点,连接、,,延长交的延长线于点若,,则的长为( )
A. B. C. D.
第II卷(非选择题)
二、填空题(本大题共4小题,共12.0分)
- 如图,在中,边的垂直平分线交边于点,交边于点若的周长为,与四边形的周长之差为,则线段的长为_________.
- 如图,在中,,点为上一点,的垂直平分线交于点,将沿着折叠,点恰好和点重合,则的度数为______.
- 如图,在中,,,分别以点,为圆心,以大于的长度为半径画弧,两弧交于点,,作直线,交于点,连接则的长度为______.
- 如图,垂直平分,交于,,,垂足为,,,则的长为______.
三、解答题(本大题共9小题,共72.0分)
- 四边形如图所示,请用尺规作图的方法,在上作一点,使得保留作图痕迹,不写作法
- 如图,在方格纸内将水平向右平移个单位得到.
补全,利用网格点和直尺画图;
图中与的关系是:______;
画出中边上的中线与高;
平移过程中,线段扫过的面积是______.
- 已知,求作:点,使,且点到的两边距离相等.
- 如图,和关于直线对称,已知,,求的度数及、的长度.
- 如图,已知,,垂直平分交于点,交于点.
求的度数;
若,,求的周长.
- 如图,按要求作图,保留痕迹,不必写作法.
利用尺规作出的平分线;
利用尺规作出线段的中点.
- 已知:如图,四边形.
求作:点,使点在四边形内部,,并且点到两边的距离相等尺规作图,不写作法,保留作图痕迹
- 如图,为的角平分线,于点,于点,交于点求证:垂直平分.
- 如图,是的平分线,点在射线上,,是直线上的两动点,点在点的右侧,且,作线段的垂直平分线,分别交直线,于点,点,连接,.
如图,当,两点都在射线上时,则线段与的数量关系是______.
如图,当,两点都在射线的反向延长线上时,线段,是否还存在中的数量关系?若存在,请写出证明过程;若不存在,请说明理由;
答案和解析
1.【答案】
【解析】
【分析】
本题考查了轴对称的知识,注意结合图形解答,不要凭空想象,实际操作一下.要击中点,则需要满足点反弹后经过的直线过点,画出反射路线即可得出答案.
【解答】
解:如图所示:
可以瞄准点击球.
故选D.
2.【答案】
【解析】解:由作图可知,垂直平分线段,
,,
又垂直平分线段,
,
故选项A,,C正确,
故选:.
利用线段的垂直平分线的性质解决问题即可.
本题考查作图复杂作图,线段的垂直平分线的性质等知识,解题的关键是读懂图象信息,灵活运用所学知识解决问题.
3.【答案】
【解析】解:由作图可知垂直平分线段,
,,
,
,,
,
,
的周长,
故选:.
利用三角形中位线定理求出,解直角三角形求出,可得结论.
本题考查作图复杂作图,线段的垂直平分线的性质,解直角三角形等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
4.【答案】
【解析】解:由作图可知,在和中,
,
≌,
,,
,,
垂直平分线段,
故A,,D正确,
故选:.
利用全等三角形的性质以及线段的垂直平分线的判定解决问题即可.
本题考查作图基本作图,全等三角形的判定和性质,线段的垂直平分线的判定等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
5.【答案】
【解析】 ,,
直线是线段的垂直平分线
,,
直线是线段的垂直平分线
当,时,直线不一定是线段的垂直平分线
,平分,
直线是线段的垂直平分线.
故选C.
6.【答案】
【解析】解:过点有且只有一条直线与直线平行,故正确,不符合题意;
B.过点有且只有一条直线与直线垂直,故正确,不符合题意;
C.在连接点和直线上各点的线段中,与直线垂直的线段最短,故正确,不符合题意;
D.直线没有垂直平分线,故错误,符合题意.
故选:.
根据垂线的定义和垂线的性质及平行线的判定对各小题分析判断即可得解.
此题主要考查了命题与定理,正确把握相关定义是解题关键.
7.【答案】
【解析】解:将沿直线折叠,
,,,
,,
,
,
,
,,
,
又,,
在和中,
,
≌,
,
,
故选:.
由折叠的性质可得,,,由“”可证≌,可得.
本题考查了翻折变换,全等三角形的判定和性质,证明≌是本题的关键.
8.【答案】
【解析】解:的周长为,,
,
由作图可知垂直平分线段,
,
的周长,
故选:.
首先证明,再证明的周长即可.
本题考查作图基本作图,线段的垂直平分线的性质等知识,解题关键是读懂图象信息,灵活运用所学知识解决问题.
9.【答案】
【解析】
【分析】
本题考查了垂直平分线的性质以及等腰三角形的性质的运用.
连接,由垂直平分线的性质,得出,得出的长,由三线合一,即可得出答案.
【解答】
解:连接,
是边的垂直平分线,
,
的最小值为,
的最小值为,
,点是的中点,
三线合一,
,
,
故选A .
10.【答案】
【解析】解:因为垂直平分,
所以.
所以.
因为平分,
所以.
所以.
11.【答案】
【解析】略
12.【答案】
【解析】
【分析】
本题考查了全等三角形的判定和性质,等腰三角形的性质,证明≌是本题的关键.
由“”可证≌,可得,,由线段垂直平分线的性质可得.
【解答】
解:为的中点,
,
,
在与中,
,
≌
,,
,
,,
,
故选:.
13.【答案】
【解析】
【分析】
此题主要考查线段的垂直平分线的性质等几何知识.线段的垂直平分线上的点到线段的两个端点的距离相等.运用线段垂直平分线定理可得,再根据已知条件“的周长为,与四边形的周长之差为”表示出线段之间的数量关系,联立关系式后求解.
【解答】
解:是边上的垂直平分线,
.
的周长为,
,
与四边形的周长之差为,
,
,
,,
得,.
故答案为.
14.【答案】
【解析】解:点在的垂直平分线上,
,
,
是的一个外角,
,
,
由折叠得:
,
,
,
,
,
,
故答案为:.
先利用线段垂直平分线的性质可得,从而可得,进而利用三角形的外角可得,然后利用折叠的性质可得,从而可得,最后根据三角形内角和定理可得,从而进行计算即可解答.
本题考查了翻折变换折叠问题,线段垂直平分线的性质,熟练掌握线段垂直平分线的性质,以及折叠的性质是解题的关键.
15.【答案】
【解析】解:由基本作图可知,是线段的垂直平分线,
,
,
,
,
,
,
,,
设,则,
在中,根据勾股定理得:
,
,
解得,
,
,
,
故答案为:.
根据像是垂直平分线的性质得到,根据三角形的周长公式计算.
本题考查的是作图基本作图,线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
16.【答案】
【解析】解:垂直平分,
,,
,,
,即,
,
,
,
,,
,
四边形为平行四边形,
,,
设,则,
在中,,
在中,,
,即,
解得:,
,
,
故AC的长为,
故答案为:.
根据线段垂直平分线的性质得到,,根据等腰三角形的性质得到,,证明,进而得到四边形为平行四边形,根据平行四边形的性质得到,,根据勾股定理列出方程,解方程得到答案.
本题考查的是平行四边形的判定和性质、线段垂直平分线的性质,掌握垂直平分线上的点到线段两端点的距离相等是解题的关键.
17.【答案】解:如图,点即为所求.
【解析】作线段的垂直平分线交于点,连接,点即为所求
本题考查作图复杂作图,线段的垂直平分线等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
18.【答案】,
【解析】解:如图,即为所求;
,.
故答案为:,;
如图,线段,即为所求;
线段扫过的面积,
故答案为:.
利用平移变换的性质分别作出,,对应点,,即可;
利用平移变换的性质判断即可;
根据三角形的中线,高的定义画出图形即可;
利用平行四边形的面积公式求解.
本题考查作图平移变换,三角形的中线,高,平行四边形的面积等知识,解题的关键是掌握平移变换性质,属于中考常考题型.
19.【答案】解:如图,作的垂直平分线和的角平分线,它们相交于点,则点为所求.
【解析】由可得点在线段的垂直平分线上,由点到的两边距离相等得到点在的平分线上,于是作的垂直平分线和的角平分线,它们的交点为点.
本题考查了作图复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了线段的垂直平分线和角平分线.
20.【答案】解:和关于直线对称,
,,D.
又,,,
,,.
【解析】略
21.【答案】解:,,
,
垂直平分
,
,
;
由知
的周长.
【解析】根据三角形内角和定理求出,根据线段垂直平分线的性质得到,求出,计算即可;
根据,三角形的周长公式计算.
本题考查的是线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
22.【答案】解:如图,射线即为所求;
如图,点即为所求.
【解析】利用尺规作出的角平分线即可;
作线段的垂直平分线交于点,点即为所求.
本题考查作图复杂作图,线段的垂直平分线等知识,解题的关键是掌握五种基本作图,属于中考常考题型.
23.【答案】解:如图,点即为所求作.
【解析】作线段的垂直平分线,作的角平分线,交于点,点即为所求作.
本题考查作图复杂作图,角平分线的性质,线段的垂直平分线的性质等知识,解题的关键是熟练掌握线段的垂直平分线的性质以及角平分线的性质定理,属于中考常考题型.
24.【答案】证明:为的角平分线,,,
.
点在线段的垂直平分线上.
在和中,
.
.
点在线段的垂直平分线上.
根据“两点确定一条直线”可知,直线即为线段的垂直平分线,
即垂直平分.
【解析】见答案.
25.【答案】
【解析】解:.
理由:如图中,连接.
垂直平分,
,
,
平分,
,
,
≌,
,
故答案为:.
存在,
理由:如图中,连接.
垂直平分,
,
,
平分,,
,
,
,
≌,
.
连接,只要证明≌即可解决问题;
存在.证明方法类似.
本题考查了线段垂直平分线,全等三角形的判定和性质,解题的关键是正确寻找全等三角形解决问题,学会用转化的思想思考问题,属于中考常考题型.









