人教A版 (2019)选择性必修 第三册7.4 二项分布与超几何分布图文ppt课件

高中数学选择性必修三

7.4.1《二项分布》同步练习

A基础练

一、选择题

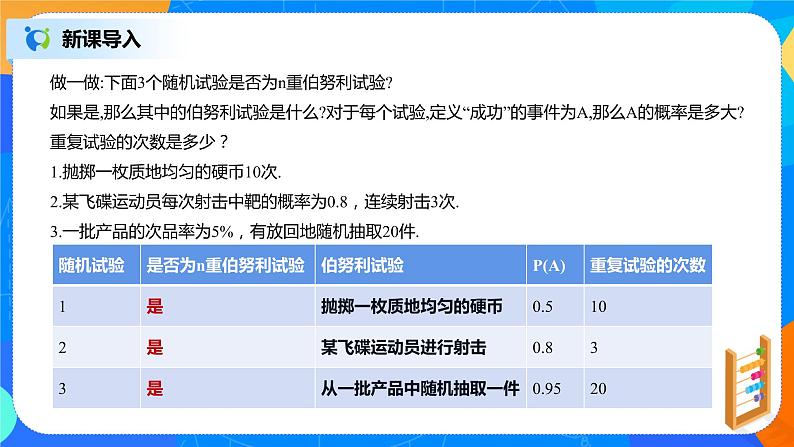
1．下列事件：①运动员甲射击一次，“射中9环”与“射中8环”；②甲､乙两运动员各射击一次，“甲射中10环”与“乙射中9环”；③甲､乙两运动员各射击一次，“甲､乙都射中目标”与“甲､乙都没射中目标”；④在相同的条件下，甲射击10次，5次击中目标.其中是伯努利试验的是（    ）

A．① B．② C．③ D．④

2．已知X～B，则P(X＝2)等于（    ）

A． B． C． D．

3．某个游戏中，一个珠子按如图所示的通道，由上至下的滑下，从最下面的六个出口出来，规定猜中者为胜，如果你在该游戏中，猜得珠子从口4出来，那么你取胜的概率为（    ）

A． B． C． D．以上都不对

4．小明准备与对手比赛，已知每局比赛小明获胜的概率为0.6，那么采用3局2胜制还是采用5局3胜制对小明有利（    ）

A．3局2胜制 B．5局3胜制 C．都一样 D．无法判断

5．（多选题）某射手射击1次，击中目标的概率是0.9，他连续射击4次，且他各次射击是否击中目标相互之间没有影响.则下列四个选项中，正确的是（    ）

A．他第3次击中目标的概率是0.9

B．他恰好击中目标3次的概率是0.930.1

C．他至少击中目标1次的概率是1-0.14

D．他恰好有连续2次击中目标的概率为30.930.1

6．（多选题）袋子中有2个黑球，1个白球，现从袋子中有放回地随机取球4次，取到白球记0分，黑球记1分，记4次取球的总分数为，则（    ）

A． B． C．X的期望 D．X的方差

二、填空题

7．现有个灯泡并联而成的闭合电路，如果在某段时间内每个灯泡能正常照明的概率都是，那么在这段时间内该电路上的灯泡至少有两个能正常照明的概率是___________.

8．某大厦的一部电梯从底层出发后只能在第、、层停靠，若该电梯在底层载有位乘客，且每位乘客在这三层的每一层下电梯是等可能的，用表示这位乘客在第层下电梯的人数，则___________.

9．已知随机变量，则___________.

10．某电视台开展有奖答题活动，每次要求答30个选择题，每个选择题有4个选项，其中有且只有一个正确答案，每一题选对得5分，选错或不选得0分，满分150分．规定满100分拿三等奖，满120分拿二等奖，满140分拿一等奖．有一个选手选对任一题的概率都是0.8，则该选手可能拿到________等奖．

三、解答题

11．某计算机程序每运行一次都随机出现一个五位的二进制数，其中的各位数中，，出现0的概率为，出现1的概率为．记，若运行该程序一次，则

（1）求的概率；

（2）求的分布列．

12．张先生到一家公司参加面试，面试的规则是；面试官最多向他提出五个问题，只要正确回答出三个问题即终止提问，通过面试根据经验，张先生能够正确回答面试官提出的任何一个问题的概率为，假设回答各个问题正确与否互不干扰．

（1）求张先生通过面试的概率；

（2）记本次面试张先生回答问题的个数为，求的分布列及数学期望

B提高练

一、选择题

1．下列说法正确的个数是（    ）

①某同学投篮的命中率为0.6，他10次投篮中命中的次数是一个随机变量，且；

②某福彩中奖概率为，某人一次买了8张，中奖张数是一个随机变量，且；

③从装有5个红球、5个白球的袋中，有放回地摸球，直到摸出白球为止，则摸球次数是随机变量，且

A．0个 B．1个 C．2个 D．3个

2．已知某种药物对某种疾病的治愈率为，现有位患有该病的患者服用了这种药物，位患者是否会被治愈是相互独立的，则恰有位患者被治愈的概率为（    ）

A． B． C． D．

3．若随机变量，则下列说法错误的是（    ）

A． B． C． D．

4．某人射击一发子弹的命中率为，现他射击19发子弹，理论和实践都表明，这19发子弹中命中目标的子弹数n的概率如下表，那么在他射击完19发子弹后，其中击中目标的子弹数最大可能是（    ）

A．14发 B．15发 C．16发 D．15或16发

5．（多选题）抛掷一枚硬币三次，若记出现“三个正面”、“三个反面”、“二正一反”、“一正二反”的概率分别为，则下列结论中正确的是（    ）

A．       B． 

C． D．

6．（多选题）某计算机程序每运行一次都随机出现一个五位二进制数（例如10100）其中A的各位数中出现0的概率为，出现1的概率为，记，则当程序运行一次时（    ）

A．X服从二项分布 B．

C．X的期望 D．X的方差

二、填空题

7．唐代诗人张若虚在《春江花月夜》中曾写道：“春江潮水连海平，海上明月共潮生．”潮水的涨落和月亮的公转运行有直接的关系，这是一种自然现象．根据历史数据，已知沿海某地在某个季节中每天出现大潮的概率均为，则该地在该季节内连续三天内，至少有两天出现大潮的概率为______________.

8．根据天文学有关知识，当且仅当一颗恒星的“赤纬”数值大于，能在扬州的夜空中看到它.下表列出了10颗恒星的“赤纬”数值：

现有四名学生从这10颗恒星中各随机选择1颗进行观测，其中有人能在扬州的夜空中看到观测目标，则的数学期望为___________.

9．假设某射手每次射击命中率相同，且每次射击之间相互没有影响.若在两次射击中至多命中一次的概率是，则该射手每次射击的命中率为______________.

10．随着电商的兴起，物流快递的工作越来越重要了，早在周代，我国便已出现快递制度，据《周礼·秋官》记载，周王朝的官职中设置了主管邮驿，物流的官员“行夫”，其职责要求是“虽道有难，而不时必达”.现某机构对国内排名前五的家快递公司的某项指标进行了轮测试(每轮测试的客观条件视为相同)，每轮测试结束后都要根据该轮测试的成绩对这家快递公司进行排名，那么跟测试之前的排名比较，这轮测试中恰好有轮测试结果都出现家公司排名不变的概率为_________.

三、解答题

11．2021年4月3日我校学生在浙江省首届少年诗词大会比赛中喜获佳绩，荣获初中组总冠军．海选环节，进入预赛的条件为：电脑随机抽取5首古诗，参赛者能够正确背诵3首及以上的进入预赛．若同学甲参赛，他背诵每一首古诗正确的概率均为．

（1）求甲进入预赛的概率；

（2）甲同学进入了预赛，此后的比赛采用积分制计算个人成绩，电脑随机抽取3首古诗，每首古诗背诵正确加2分，错误减1分．由于难度增加，甲背诵每首古诗正确的概率为，设甲的得分为，请写出的分布列，并求出甲得分的数学期望．

12．冠状病毒是一个大型病毒家族，已知可引起感冒以及中东呼吸综合征(MERS)和严重急性呼吸综合征(SARS)等较严重疾病，而新型冠状病毒(nCoV)是以前从未在人体中发现的冠状病毒新毒株人，感染了新型冠状病毒后常见体征有呼吸道症状，发热、咳嗽、气促和呼吸困难等在较严重病例中，感染可导致肺炎，严重急性呼吸综合征，肾衰竭，甚至死亡．假如某医药研究机构合成了甲、乙两种抗“新冠病毒”的药物．经试验，服用甲、乙两种药物痊愈的概率分别为，现已进入药物临床试用阶段．每个试用组由4位该病毒的感染者组成．其中2人试用甲种抗病毒药物，2人试用乙种抗病毒药物．如果试用组中，甲种抗病毒药物治愈人数超过乙种抗病毒药物的治愈人数，则称该组为“甲类组”．

（1））求一个试用组为“甲类组”的概率；

（2）观察3个试用组，用表示这3个试用机组“甲类组”的个数，求的分布列和数学期望．

同步练习答案

A基础练

一、选择题

1．【答案】D

【详解】①和③符合互斥事件的概念，是互斥事件；②是相互独立事件；④是独立重复试验；所以只有④符合题意，故选：D.

2．【答案】D

【详解】因为X～B，所以.故选：D

3．【答案】C

【详解】解：从入口到出口4共有种走法，其中每一岔口的概率都是

所以珠子从口4出来的概率为，故选：C

4．【答案】B

【详解】采用5局3胜制：

采用3局2胜制：，所以对小明来说，在五局三胜制中获胜的概率比较大.，故选：B.

5．【答案】AC

【详解】∵射击一次击中目标的概率是0.9，∴第3次击中目标的概率是0.9，∴A正确;∵连续射击4次，且各次射击是否击中目标相互之间没有影响，∴本题是一个独立重复试验，根据独立重复试验的公式得到恰好击中目标3次的概率是0.930.1，∴B不正确;∵至少击中目标1次的概率是10.14，∴C正确;∵恰好有连续2次击中目标的概率为30.920.12，∴D不正确.故选：AC.

6．【答案】ACD

【详解】从袋子中有放回地随机取球4次，则每次取球互不影响，并且每次取到的黑球概率相等，又取到黑球记1分，取4次球的总分数，即为取到黑球的个数，所以随机变量服从二项分布，故A正确；，记其概率为，故B错误；

因为，所以的期望，故C正确；因为，所以的方差，故D正确．故选：ACD．

二、填空题

7．【答案】

【详解】根据题意可知，这段时间内该电路上有两个或三个灯泡能正常照明，

因此，所求事件的概率为.

8．【答案】

【详解】由题意可知，因此，.

9．【答案】

【详解】由题意知：，易知，

∴.

10．【答案】二

【详解】由题意，选手选对任一题的概率都是0.8，所以选手选对题的个数服从二项分布，即，所以，可得（分），所以可能拿到二等奖.

三、解答题

11．【解析】

解：（1）已知，要使，只需后四位中出现2个1和2个0．

所以．

（2）令，则．

易知，，所以的可能取值为．

，，

，，

．

所以的分布列为

12．【答案】（1）；（2）分布列见解析；期望为．

【详解】解：记张先生第i次答对面试官提出的问题为事件，则，张先生前三个问题均回答正确为事件；前三个问题回答正确两个且第四个又回答正确为事件，前四个问题回答正确两个且第五个又回答正确为事件，张先生通过面试为事件．则

根据题意，得

因为事件互斥，所以

即张先生能够通过面试的概率为

根据题意，

表明前面三个问题均回答错误(淘汰)或均回答正确(通过)，

所以

表明前面三个问题中有两个回答错误且第四个问题又回答错误(淘汰)，或者前面三个问题中有两个回答正确且第四个问题回答正确(通过)，

所以

表明前面四个问题中有两个回答错误、两个回答正确，

所以

所以的分布列为：

故

B提高练

一、选择题

1．【答案】C

【详解】①某同学投篮的命中率为0.6，该同学投篮10次，是一个独立重复试验，所以他10次投篮中命中的次数是一个随机变量，且，所以该命题正确；②某福彩中奖概率为，某人一次买了8张，相当于买了8次，每次中奖的概率都为，相当于做了8次独立重复试验，中奖张数是一个随机变量，且，所以该命题正确；③从装有5个红球、5个白球的袋中，由于它是有放回地摸球，直到摸出白球为止，所以它不是一个独立重复性试验，因为当时，概率为，当时，概率为，当时，概率为，依次类推，即每次试验摸到白球的概率不相等，所以它不是独立重复性试验，所以不服从,所以该命题错误.故选：C

2．【答案】B

【详解】由已知位患者被治愈是相互独立的，每位患者被治愈的概率为，则不被治愈的概率为，所以位患者中恰有1为患者被治愈的概率为，故选：B

3．【答案】D

【详解】因为随机变量，所以，，所以，，D项错误，故选：D.

4．【答案】D

【详解】根据题意，设第k发子弹击中目标的概率最大，而19发子弹中命中目标的子弹数n的概率（，，，，），

则有且，

即 ，解可得 ，

即第15或16发子弹击中目标的可能性最大，则他射完19发子弹后，击中目标的子弹最可能是第15或16发.故选：D．

5．【答案】CD

【详解】由题意，抛掷一枚硬币三次，若记出现“三个正面”、“三个反面”、“二正一反”、“一正二反”的概率分别为，根据独立重复试验的概率计算公式，

可得：，

由，故A是错误的；由，故B是错误的；

由，故C是正确的；由，故D是正确的.故选：CD

6．【答案】ABC

【详解】解：由于二进制数的特点知每一个数位上的数字只能填0，1，

且每个数位上的数字再填时互不影响，故以后的5位数中后4位的所有结果有4类：

①后4个数出现0，，记其概率为；

②后4个数位只出现1个1，，记其概率为；

③后4位数位出现2个1，，记其概率为，

④后4个数为上出现3个1，记其概率为，

⑤后4个数为都出现1，，记其概率为，

故，故正确；又，故正确；

，，故正确；，的方差，故错误．故选：．

二、填空题

7．【答案】

【详解】该地在该季节内连续三天内，至少有两天出现大潮包括两天或三天出现大潮，

有两天出现大潮概率为，有三天出现大潮概率为，

所以至少有两天出现大潮的概率为，故选：A.

8．【答案】3.6

【详解】大于的有9个，小于的有1个在扬州能看到的概率为，，.

9．【答案】

【详解】设该射手射击命中的概率为，两次射击命中的次数为，则，由题可知：，即，解得.

10．【答案】

【详解】解：首先，在一轮测试中家快递公司进行排名与测试之前的排名比较出现家公司排名不变的概率为，其次，3轮测试每次发生上述情形的概率均为,故轮测试中恰好有轮测试结果都出现家公司排名不变的概率为.

三、解答题

11．【答案】(1) ；(2)见解析；甲得分的数学期望为.

【详解】解：(1)记“甲进入预赛”为事件，则

故甲进入预赛的概率的概率为.

(2) 的所有可能取值为，，，，则

；；

；，

所以的分布列为

所以.

12．【答案】（1）；（2）分布列见解析；期望为．

【详解】解（1）设表示事件“一个试验组中，服用甲种抗病毒药物有效的人数人”，，

表示事件“一个试验组中，服乙有效的人有人”，

依题意有

所求的概率为

（2）的可能值为，且

，

，

，

，

的分布列为

数学期望