初中数学人教版八年级上册13.1.1 轴对称导学案

这是一份初中数学人教版八年级上册13.1.1 轴对称导学案，共19页。学案主要包含了学习目标，知识网络，要点梳理，典型例题，思路点拨，总结升华，答案与解析，特殊情况，探索结论等内容，欢迎下载使用。
轴对称全章复习与巩固（提高）

【学习目标】
1. 认识轴对称、轴对称图形，理解轴对称的基本性质及它们的简单应用；
2. 了解垂直平分线的概念，并掌握其性质；
3. 了解等腰三角形、等边三角形的有关概念，并掌握它们的性质以及判定方法.
【知识网络】

【要点梳理】
【高清课堂：389304 轴对称复习，本章概述】
要点一、轴对称
1.轴对称图形和轴对称　　
（1）轴对称图形
如果一个图形沿着某一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形，这条直线就是它的对称轴.轴对称图形的性质：轴对称图形的对称轴，是任何一对对应点所连线段的垂直平分线.
（2）轴对称
　　定义：把一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线对称，这条直线叫做对称轴.成轴对称的两个图形的性质：
①关于某条直线对称的两个图形形状相同，大小相等，是全等形；
②如果两个图形关于某条直线对称，则对称轴是任何一对对应点所连线段的垂直平分线；
③两个图形关于某条直线对称，如果它们的对应线段或延长线相交，那么它们的交点在对称轴上.
（3）轴对称图形与轴对称的区别和联系
区别: 轴对称是指两个图形的位置关系，轴对称图形是指具有特殊形状的一个图形；轴对称涉及两个图形，而轴对称图形是对一个图形来说的.联系：如果把一个轴对称图形沿对称轴分成两个图形，那么这两个图形关于这条轴对称；如果把成轴对称的两个图形看成一个整体，那么它就是一个轴对称图形．
2.线段的垂直平分线
线段的垂直平分线的性质：线段垂直平分线上的点与这条线段两个端点的距离相等.反过来，与一条线段两个端点距离相等的点，在这条线段的垂直平分线上.
要点二、作轴对称图形
1.作轴对称图形
（1）几何图形都可以看作由点组成，我们只要分别作出这些点关于对称轴的对应点，再连接这些点，就可以得到原图形的轴对称图形；
（2）对于一些由直线、线段或射线组成的图形，只要作出图形中的一些特殊点（如线段端点）的对称点，连接这些对称点，就可以得到原图形的轴对称图形.
2.用坐标表示轴对称
点（,）关于轴对称的点的坐标为（,－）；点（,）关于轴对称的点的坐标为（－,）；点（,）关于原点对称的点的坐标为（－,－）.
要点三、等腰三角形
1.等腰三角形
　　（1）定义：有两边相等的三角形，叫做等腰三角形.
（2）等腰三角形性质
　①等腰三角形的两个底角相等，即“等边对等角”；
②等腰三角形顶角的平分线、底边上的中线与底边上的高线互相重合（简称“三线合一”）.特别地，等腰直角三角形的每个底角都等于45°.
（3）等腰三角形的判定
如果一个三角形有两个角相等，那么这两个角所对的边也相等（即“等角对等　 　　边”）.
2.等边三角形
　　（1）定义：三条边都相等的三角形，叫做等边三角形.
（2）等边三角形性质：等边三角形的三个角相等，并且每个角都等于60°.　　
（3）等边三角形的判定：
①三条边都相等的三角形是等边三角形；
②三个角都相等的三角形是等边三角形；
③有一个角为 60°的等腰三角形是等边三角形.
3.直角三角形的性质定理：
在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半.
【典型例题】
类型一、轴对称的性质与应用
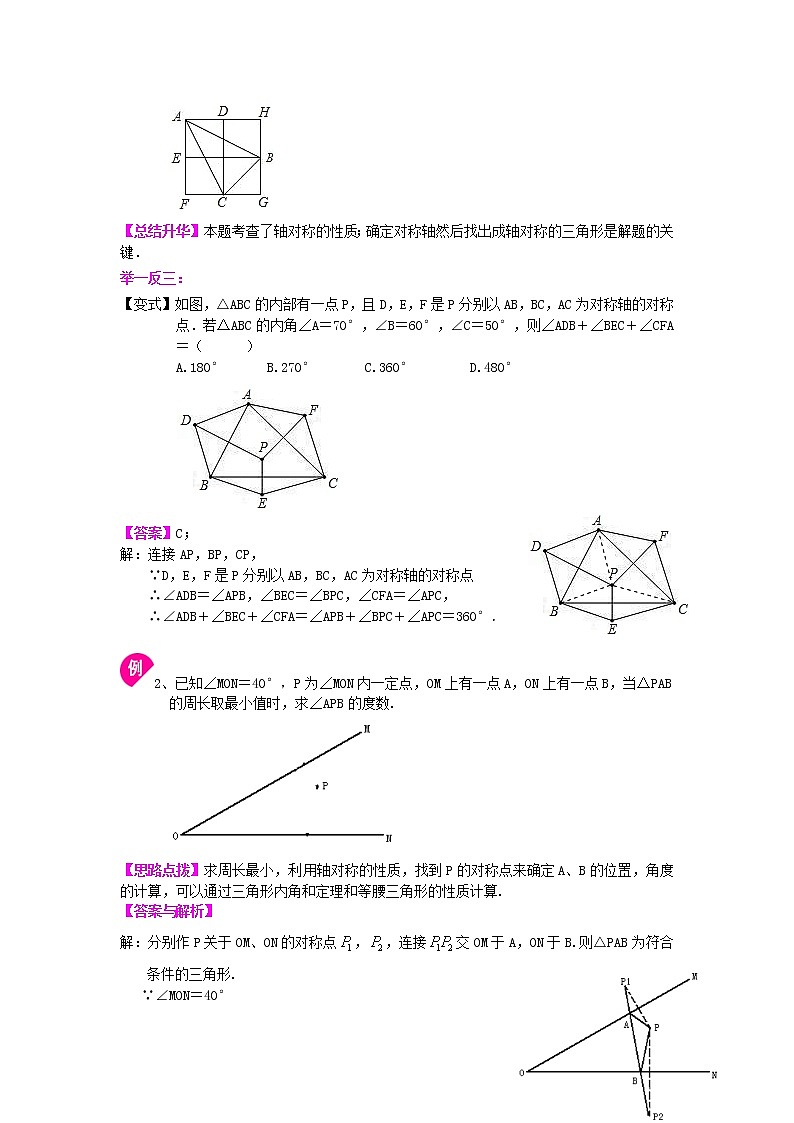
1、如图，由四个小正方形组成的田字格中，△ABC的顶点都是小正方形的顶点．在田字格上画与△ABC成轴对称的三角形，且顶点都是小正方形的顶点，则这样的三角形（不包含△ABC本身）共有（　　）
A.1个 B.2个 C.3个 D.4个

【思路点拨】分别以正方形的对角线和田字格的十字线为对称轴，来找三角形.
【答案】C；
【解析】先把田字格图标上字母如图，确定对称轴找出符合条件的三角形，再计算个数．
△HEC与△ABC关于CD对称；△FDB与△ABC关于BE对称；△GED与△ABC关于HF对称；关于AG对称的是它本身．所以共3个．

【总结升华】本题考查了轴对称的性质；确定对称轴然后找出成轴对称的三角形是解题的关键．
举一反三：
【变式】如图，△ABC的内部有一点P，且D，E，F是P分别以AB，BC，AC为对称轴的对称点．若△ABC的内角∠A＝70°，∠B＝60°，∠C＝50°，则∠ADB＋∠BEC＋∠CFA＝（　 　）
A.180° B.270° C.360° D.480°

【答案】C；
解：连接AP，BP，CP，
∵D，E，F是P分别以AB，BC，AC为对称轴的对称点
∴∠ADB＝∠APB，∠BEC＝∠BPC，∠CFA＝∠APC，
∴∠ADB＋∠BEC＋∠CFA＝∠APB＋∠BPC＋∠APC＝360°．

2、已知∠MON＝40°，P为∠MON内一定点，OM上有一点A，ON上有一点B，当△PAB的周长取最小值时，求∠APB的度数.

【思路点拨】求周长最小，利用轴对称的性质，找到P的对称点来确定A、B的位置，角度的计算，可以通过三角形内角和定理和等腰三角形的性质计算.
【答案与解析】
解：分别作P关于OM、ON的对称点，，连接交OM于A，ON于B.则△PAB为符合条件的三角形.
∵∠MON＝40°
　 ∴∠＝140°.
∠＝∠PAB,∠＝∠PBA.
∴ (∠PAB＋∠PBA)＋∠APB＝140°
∴∠PAB＋∠PBA＋2∠APB＝280°
∵∠PAB＝∠＋∠, ∠PBA＝∠＋∠
∴∠＋∠＋∠＝180°
∴∠APB＝100°
【总结升华】将实际问题抽象或转化为几何模型，将周长的三条线段的和转化为一条线段，这样取得周长的最小值.
举一反三：
【变式】（2015•乐陵市模拟）（1）如图1，直线同侧有两点A、B，在直线上求一点C，使它到A、B之和最小．（保留作图痕迹不写作法）
（2）知识拓展：如图2，点P在∠AOB内部，试在OA、OB上分别找出两点E、F，使△PEF周长最短（保留作图痕迹不写作法）
（3）解决问题：①如图3，在五边形ABCDE中，在BC，DE上分别找一点M，N，使得△AMN周长最小（保留作图痕迹不写作法）
②若∠BAE=125°，∠B=∠E=90°，AB=BC，AE=DE，∠AMN+∠ANM的度数为　 　．

【答案】解：（1）作A关于直线MN的对称点E，连接BE交直线MN于C，连接AC，BC，
则此时C点符合要求．

（2）作图如下：

（3）①作图如下：

②∵∠BAE=125°，
∴∠P+∠Q=180°﹣125°=55°，
∵∠AMN=∠P+∠PAM=2∠P，∠ANM=∠Q+∠QAN=2∠Q，
∴∠AMN+∠ANM=2（∠P+∠Q）=2×55°=110°．
3、（2016春•浦东新区期末）在直角坐标平面内，已知在y轴与直线x=3之间有一点M（a，3），如果该点关于直线x=3的对称点M的坐标为（5，3），那么a的值为（　　）
A．4 B．3 C．2 D．1
【思路点拨】根据题意得出对称点到直线x=3的距离为2，再利用对称点的性质得出答案．
【答案】D；
【解析】解：∵该点关于直线x=3的对称点N的坐标为（5，3），
∴对称点到直线x=3的距离为2，
∵点M（a，3）到直线x=3的距离为2，
∴a=1
【总结升华】此题主要考查了坐标与图形的性质，根据题意得出对称点到直线x=3的距离是解题关键．
举一反三：
【变式1】如图，若直线经过第二、四象限，且平分坐标轴的夹角，Rt△AOB与Rt△关于直线对称，已知A（1，2），则点的坐标为（　　）
A.（－1，2） B.（1，－2） C.（－1，－2） D.（－2，－1）

【答案】D；
提示：因为Rt△AOB与Rt△关于直线对称，所以通过作图可知，的坐标是（－2，－1）．
【高清课堂：389304 轴对称复习：例10】
【变式2】如图，ΔABC中，点A的坐标为（0，1），点C的坐标为（4，3），点B的坐标为
（3，1），如果要使ΔABD与ΔABC全等，求点D的坐标．

【答案】
解：满足条件的点D的坐标有3个（4，－1）；（－1，－1）；（－1，3）.
类型二、等腰三角形的综合应用
4、如图①，△ABC中．AB=AC，P为底边BC上一点，PE⊥AB，PF⊥AC，CH⊥AB，垂足分别为E、F、H．易证PE+PF=CH．证明过程如下：

如图①，连接AP．
∵PE⊥AB，PF⊥AC，CH⊥AB，
∴=AB•PE，=AC•PF，=AB•CH．
又∵，
∴AB•PE+AC•PF=AB•CH．∵AB=AC，∴PE+PF=CH．
（1）如图②，P为BC延长线上的点时，其它条件不变，PE、PF、CH又有怎样的数量关系？请写出你的猜想，并加以证明：
（2）填空：若∠A=30°，△ABC的面积为49，点P在直线BC上，且P到直线AC的距离为PF，当PF=3时，则AB边上的高CH=______.点P到AB边的距离PE=________.
【答案】7；4或10；
【解析】
解：（1）如图②，PE=PF+CH．证明如下：
∵PE⊥AB，PF⊥AC，CH⊥AB，
∴=AB•PE，=AC•PF，=AB•CH，
∵=+，
∴AB•PE=AC•PF+AB•CH，
又∵AB=AC，
∴PE=PF+CH；

（2）∵在△ACH中，∠A=30°，
∴AC=2CH．
∵=AB•CH，AB=AC，
∴×2CH•CH=49，
∴CH=7．
分两种情况：
①P为底边BC上一点，如图①．
∵PE+PF=CH，
∴PE=CH-PF=7-3=4；
②P为BC延长线上的点时，如图②．
∵PE=PF+CH，
∴PE=3+7=10．
故答案为7；4或10．
【总结升华】本题考查了等腰三角形的性质与三角形的面积，难度适中，运用面积证明可使问题简便，（2）中分情况讨论是解题的关键．
5、已知，如图，∠1＝12°，∠2＝36°，∠3＝48°，∠4＝24°. 求的度数．

【答案与解析】
A
C
D
1
2
3
B
5
E
解：将沿AB翻折，得到，连结CE，
则，
∴∠1＝∠5＝12°.
∴60°
∵48°∴．
又∵∠2＝36°，72°，
∴
∴BE＝BC
∴为等边三角形.
∴
又垂直平分BC．
∴AE平分．
∴30°
∴∠ADB＝30°
【总结升华】直接求很难，那就想想能不能通过翻折或旋转构造一个与全等的三角形，从而使其换个位置，看看会不会容易求．
举一反三：
【变式】在△ABC中，AB＝AC，∠BAC＝80°，D为形内一点，且∠DAB＝∠DBA＝10°，
求∠ACD的度数.

【答案】　　　　　　　　　　　　　　　　　
解：作D关于BC中垂线的对称点E，连结AE，EC，DE
　　　 　　∴△ABD≌△ACE
　　　 　　∴AD＝AE, ∠DAB＝∠EAC＝10°
　　　 　　∵∠BAC=80°，
∴∠DAE＝60°，△ADE为等边三角形
∴∠AED＝60°
　　　 　　∵∠DAB＝∠DBA＝10°
　　　 　　∴AD＝BD＝DE＝EC
　　　 　　∴∠AEC＝160°，
　　　 　　∴∠DEC＝140°
　　 　　　∴∠DCE＝20°
　　　 　　∴∠ACD＝30°
类型三、等边三角形的综合应用
6、（秋•辛集市期末）已知，在等边三角形ABC中，点E在AB上，点D在CB的延长线上，且ED=EC．
（1）【特殊情况，探索结论】
如图1，当点E为AB的中点时，确定线段AE与DB的大小关系，请你直接写出结论：AE
　 　DB（填“＞”、“＜”或“=”）．
（2）【特例启发，解答题目】
如图2，当点E为AB边上任意一点时，确定线段AE与DB的大小关系，请你直接写出结论，AE　 　DB（填“＞”、“＜”或“=”）；理由如下，过点E作EF∥BC，交AC于点F．（请你完成以下解答过程）．
（3）【拓展结论，设计新题】
在等边三角形ABC中，点E在直线AB上，点D在直线CB的延长线上，且ED=EC，若△ABC的边长为1，AE=2，求CD的长（请你画出相应图形，并直接写出结果）．

【思路点拨】（1）由E为等边三角形AB边的中点，利用三线合一得到CE垂直于AB，且CE为角平分线，由ED=EC，利用等边对等角及等腰三角形的性质得到一对角相等，利用等角对等边即可得证；
（2）AE=DB，理由如下，过点E作EF∥BC，交AC于点F，由三角形ABC为等边三角形，得到三角形AEF为等边三角形，进而得到AE=EF=AF，BE=FC，再由ED=EC，以及等式的性质得到夹角相等，利用SAS得到三角形BDE与三角形EFC全等，利用全等三角形对应边相等得到DB=EF，等量代换即可得证；
（3）点E在AB延长线上时，如图所示，同理可得△DBE≌△EFC，由BC+DB求出CD的长即可．
【答案与解析】
解：（1）当E为AB的中点时，AE=DB；
（2）AE=DB，理由如下：
过点E作EF∥BC，交AC于点F，
证明：∵△ABC为等边三角形，
∴△AEF为等边三角形，
∴AE=EF，BE=CF，
∵ED=EC，
∴∠D=∠ECD，
∵∠DEB=60°﹣∠D，∠ECF=60°﹣∠ECD，
∴∠DEB=∠ECF，
在△DBE和△EFC中，
，
∴△DBE≌△EFC（SAS），
∴DB=EF，
则AE=DB；
（3）点E在AB延长线上时，如图所示，同理可得△DBE≌△EFC，
∴DB=EF=2，BC=1，
则CD=BC+DB=3．

【总结升华】此题考查了等边三角形的判定与性质，全等三角形的判定与性质，以及等腰三角形的性质，熟练掌握等边三角形的判定与性质是解本题的关键．

【巩固练习】
一.选择题
1. 如图所示，将矩形纸片先沿虚线AB按箭头方向向右对折，接着对折后的纸片沿虚线CD向下对折，然后剪下一个小三角形，再将纸片打开，则打开后的展开图是（ ）

2. 如图，将正方形纸片ABCD折叠，使边AB、CB均落在对角线BD上，得折痕BE、BF，则∠EBF的大小为( )
A. 15° B. 30° C. 45° D. 60°

3．（2016秋·诸城市月考）下列语句中，正确的有（ ）
①关于一条直线对称的两个图形一定能重合；
②两个能重合的图形一定关于某条直线对称；
③一个轴对称图形不一定只有一条对称轴；
④两个轴对称图形的对应点一定在对称轴的两侧；
⑤角平分线上任意一点到角的两边的线段长相等.
A．1个 B. 2个 C. 3个 D. 4个
4. 小明从镜中看到电子钟示数是，则此时时间是（ ）
A.12：01 B.10：51 　　 　 C.11：59 D.10：21
5. 已知A（4，3）和B是坐标平面内的两个点，且它们关于直线＝－3轴对称，则平面内点B的坐标是（ ）
A.（1，3） B.（－10，3） C.（4，3） D.（4，1）
6．（•本溪校级二模）如图，过边长为1的等边△ABC的边AB上一点P，作PE⊥AC于E，Q为BC延长线上一点，当PA=CQ时，连PQ交AC边于D，则DE的长为（　　）

　 A． B． C． D． 不能确定
7. 如图，将△沿、、翻折，三个顶点均落在点处.若，则 的度数为（ ）
A. 49° B. 50° C. 51° D. 52°

8. 如图, △ABC中, ∠ACB＝90°, ∠ABC＝60°, AB的中垂线交BC的延长线于D,交AC于E, 已知DE＝2.AC的长为（ ）
A.2 B.3 C. 4 D.5


二.填空题
9. 如图，在矩形纸片ABCD中，AB＝2，点E在BC上，且AE＝CE．若将纸片沿AE折叠，点B恰好与AC上的点重合，则AC＝ ．

10. 在同一直角坐标系中，A（＋1，8）与B（－5，－3）关于轴对称，则＝___________，＝___________.
11．如图所示，△ABC中，已知∠B和∠C的平分线相交于点F，过点F作DE∥BC，交AB于点D，交AC于点E，若BD＋CE＝9，线段DE＝_______．

12. （2016春•淄博期中）如图，∠BAC=30°，AM是∠BAC的平分线，过M作ME∥BA交AC于E，作MD⊥BA，垂足为D，ME=10cm，则MD=　 　．

13．如图所示，在△ABC中，AB＝AC，点O在△ABC内，且∠OBC＝∠OCA，∠BOC＝110°，求∠A的度数为________．

14. 如图，在四边形ABCD中，∠A＝90°，AD＝4，连接BD，BD⊥CD，∠ADB＝∠C.若P是BC边上一动点，则DP长的最小值为 .

15.（•徐州模拟）如图，△ABC的面积为4cm2，BP平分∠ABC，且AP⊥BP于P，则△PBC的面积为　 　cm2．

16. 如图，六边形ABCDEF的六个内角都相等．若AB＝1，BC＝CD＝3，DE＝2，则这个六边形的周长等于_________。


三.解答题
17．如图所示，△ABC中，D，E在BC上，且DE＝EC，过D作DF∥BA，交AE于点F，DF＝AC，求证AE平分∠BAC．



18. 如图所示，等边三角形ABC中，AB＝2，点P是AB边上的任意一点（点P可以与点A重合，但不与点B重合），过点P作PE⊥BC，垂足为E，过E作EF⊥AC，垂足为F，过F作FQ⊥AQ，垂足为Q，设BP＝，AQ＝．
（1）写出与之间的关系式；
（2）当BP的长等于多少时，点P与点Q重合？


19．（•清河区三模）阅读理解：
如图1，在△ABC的边AB上取一点P，连接CP，可以把△ABC分成两个三角形，如果这两个三角形都是等腰三角形，我们就称点P是△ABC的边AB上的和谐点．
解决问题：
（1）如图2，△ABC中，∠ACB=90°，试找出边AB上的和谐点P，并说明理由．
（2）已知∠A=40°，△ABC的顶点B在射线l上（图3），点P是边AB上的和谐点，请在图3中画出所有符合条件的B点，并写出相应的∠B的度数．


20．已知，∠BAC＝90º，AB＝AC，D为AC边上的中点，AN⊥BD于M，交BC于N.
求证：∠ADB＝∠CDN


【答案与解析】
一.选择题
1. 【答案】D；
【解析】作出对称轴，将图形还原即可.
2. 【答案】C；
【解析】由题意，∠ABE＝∠DBE＝∠DBF＝∠FBC，所以∠EBF＝∠ABC＝45°，故选C．
3. 【答案】B；
【解析】①关于一条直线对称的两个图形一定能重合，正确；
②两个能重合的图形一定关于某条直线对称，错误；
③一个轴对称图形不一定只有一条对称轴，正确；
④两个轴对称图形的对应点一定在对称轴的两侧，错误；
⑤角平分线上任意一点到角的两边的线段长相等，错误；
综上所述，正确的只有①③共2个.
4. 【答案】B；
5. 【答案】B；
【解析】点B的纵坐标和点A一样，（横坐标＋4）÷2＝－3，解得横坐标为－10.
6. 【答案】B；
【解析】解：过P作PF∥BC交AC于F．
∵PF∥BC，△ABC是等边三角形，
∴∠PFD=∠QCD，△APF是等边三角形，
∴AP=PF=AF，
∵PE⊥AC，
∴AE=EF，
∵AP=PF，AP=CQ，
∴PF=CQ．
∵在△PFD和△QCD中，
，
∴△PFD≌△QCD（AAS），
∴FD=CD，
∵AE=EF，
∴EF+FD=AE+CD，
∴AE+CD=DE=AC，
∵AC=1，
∴DE=．
故选：B．

7. 【答案】C；
【解析】∠A＝∠DOE,∠B＝∠HOG,∠C＝∠EOF,所以∠2＝360°－180°－129°＝51°.
8. 【答案】B；
【解析】连接AD，易证三角形ABD为等边三角形，CE＝DE＝1，AE＝DE＝2，所以AC＝AE＋CE＝2＋1＝3.
二.填空题
9. 【答案】4；
【解析】因为AE＝CE，∠＝90°，所以为AC的中点.AC＝2AB＝4.
10.【答案】；
【解析】由题意＋1＝－5，3－＝8，解得.
11．【答案】9；
【解析】因为DE∥BC， 所以∠DFB＝∠FBC，∠EFC＝∠FCB， 因为∠FBC＝∠FBD，∠FCB＝∠FCE， 所以∠FBD＝∠DFB，∠FCE＝∠EFC， 所以BD＝DF，CE＝EF， 所以BD＋CE＝DF＋FE＝DE，所以DE＝BD＋CE＝9．
12.【答案】5cm；
【解析】过M作MF⊥AC于F，∵AM是∠BAC的角平分线，∴MD=MF，∠BAM=∠CAM，
∵ME∥BA，∴∠AME=∠BAM，∴∠CAM=∠AME=∠BAC=×30°=15°，
∵∠CEM是△AME的外角，∴∠CEM=∠CAM+∠AME=15°+15°=30°，
在Rt△MEF中，∠FEM=30°，∴MF=ME=×10=5cm，∴MD=MF=5cm．

13．【答案】40°；
【解析】∵AB＝AC，所以∠ABC＝∠ACB， 又∵∠OBC＝∠OCA，
∴∠ABC＋∠ACB＝2（∠OBC＋∠OCB）， ∵∠BOC＝110°，
∴∠OBC＋∠OCB＝70°， ∴∠ABC＋∠ACB＝140°，
∴∠A＝180°－（∠ABC＋∠ACB）＝40°．
14.【答案】4；
【解析】过D作DP⊥BC，此时DP长的最小值是.因为∠ABD＝∠CBD，所以AD＝DP＝4.
15.【答案】2；
【解析】解：如图，延长AP交BC于D，
∵BP平分∠ABC，AP⊥BP，
∴AP=PD，
∴S△ABP=S△DBP，S△ACP=S△DCP，
∴△PBC的面积=S△DBP+S△DCP=S△ABC=×4=2cm2．
故答案为：2．

16.【答案】15；
【解析】因为六边形ABCDEF的六个内角都相等为120°，每个外角都为60°，向外作三个三角形，进而得到四个等边三角形，如图，设AF＝，EF＝，则有＋1＋3＝＋＋2＝3＋3＋2＝8所以＝4，＝2，六边形ABCDEF的周长＝1＋3＋3＋2＋2＋4＝15.

三.解答题
17．【解析】
证明：延长FE到G，使EG＝EF，连接CG，
在△DEF和△CEG中，
ED＝EC，∠DEF＝∠CEG，FE＝EG，
∴△DEF≌△CEG，
∴DF＝GC，∠DFE＝∠G，
∵DF∥AB，∴∠DFE＝∠BAE，
∵DF＝AC，∴GC＝AC，
∴∠G＝∠CAE，
∴∠BAE＝∠CAE，即AE平分∠BAC．

18．【解析】
解：（1）∵△ABC为等边三角形，
∴∠A＝∠B＝∠C＝60°，AB＝BC＝CA＝2．
在△BEP中，∵PE⊥BE，∠B＝60°，
∴∠BPE＝30°，
而BP＝，∴BE＝，EC＝2－，
在△CFE中，∵∠C＝60°，EF⊥CF，
∴∠FEC＝30°，所以FC＝1－x，
同理在△FAQ中，可得AQ＝＋，
而AQ＝，所以＝＋（0＜≤2）．
（2）当点P与点Q重合时，有AQ＋BP＝AB＝2，
∴＋＝2，所以
解得＝．
∴当BP的长为时，点P与点Q重合．
19．【解析】
解：（1）AB边上的和谐点为AB的中点；理由如下：∵P是AB的中点，∴PC=AB=PA=PB，∴△ACP和△BCP是等腰三角形；
（2）所有符合条件的点B有3个，如图3所示：∠B的度数为35°、50°、80°．

20.【解析】
证明：作∠BAC的角平分线交BD于H
∴∠BAH＝∠CAH＝45º
∵AB＝AC,
∴∠ABC＝∠C＝45 º
∴∠BAH＝∠C
∵AN⊥BD于M，
∴∠AMD＝90º
∴∠NAD＋∠ADB＝90º
∵∠BAC＝90º
∴∠ABD＋∠ADB＝90º
∴∠ABD＝∠NAC
在△ABH与△CAN中

∴△ABH≌△CAN
∴AH＝CN
∵D为AC边上的中点
∴AD＝CD
在△AHD与△CND中

∴△AHD≌△CND
∴∠ADB＝∠CDN．