

初中数学北师大版九年级下册第二章 二次函数综合与测试学案
展开九(下)第二章 二次函数(第十四周周末教案 课时27)
第一节 二次函数
知识点一、二次函数的定义
一般地,形如 y=ax2+bx+c (a、b、c是常数,a≠0) 的叫做x的二次函数.把y=ax2+bx+c(a、b、c是常数,a≠0)叫做二次函数的一般式,其中ax2、bx、c分别是 二 次项、 一 次项和 常数 项.自变量x的取值范围是全体实数。
【例1】 下列函数一定是二次函数的是( )
A. B. C. y=(x+1)2-x2 D. y=ax2+bx+c
【例2】 若是关于x的二次函数,则m=( )
A. B. 3 C. -1 D. 3或-1
知识点二、根据实际问题列二次函数表达式
【例3】在某市开展的环境创优活动中,某居民小区要在一块靠墙(墙长15米)的空地上修建一个矩形花园ABCD,花园的一边靠墙, 另三 边用总长为40m的栅栏围成,若设花园平行于墙的一边长为x(m),花园的面积为y(m2).(1)求y与x之间的函数关系式,并写出自变量 x的取值范围;(2)满足条件的花园面积能达到200m2吗?若能,求出此时x的值,若不能,说明理由.
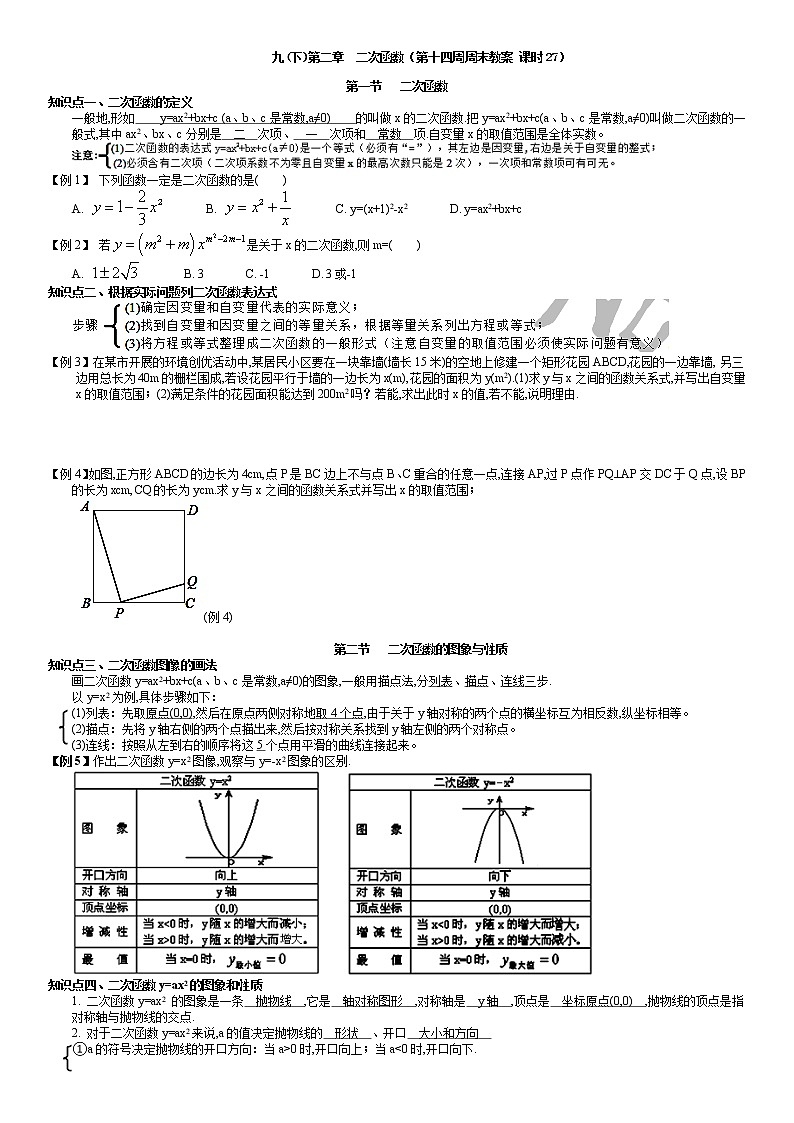
【例4】如图,正方形ABCD的边长为4cm,点P是BC边上不与点B、C重合的任意一点,连接AP,过P点作PQ⊥AP交DC于Q点,设BP的长为xcm,CQ的长为ycm.求y与x之间的函数关系式并写出x的取值范围;
(例4)
第二节 二次函数的图象与性质
知识点三、二次函数图像的画法
画二次函数y=ax2+bx+c(a、b、c是常数,a≠0)的图象,一般用描点法,分列表、描点、连线三步.
以y=x2为例,具体步骤如下:
(1)列表:先取原点(0,0),然后在原点两侧对称地取4个点,由于关于y轴对称的两个点的横坐标互为相反数,纵坐标相等。
(2)描点:先将y轴右侧的两个点描出来,然后按对称关系找到y轴左侧的两个对称点。
(3)连线:按照从左到右的顺序将这5个点用平滑的曲线连接起来。
【例5】作出二次函数y=x2图像,观察与y=-x2图象的区别.
知识点四、二次函数y=ax2的图象和性质
1. 二次函数y=ax2 的图象是一条 抛物线 ,它是 轴对称图形 ,对称轴是 y轴 ,顶点是 坐标原点(0,0) ,抛物线的顶点是指对称轴与抛物线的交点.
2. 对于二次函数y=ax2来说,a的值决定抛物线的 形状 、开口 大小和方向
①a的符号决定抛物线的开口方向:当a>0时,开口向上;当a<0时,开口向下.
②a的绝对值决定抛物线的形状和开口大小:越大时抛物线的开口反而越小,且图象越靠近y轴。
3. 增减性及最值:
①当a>0时,.在对称轴 左边 ,曲线自左向右 下降 ,y随x的增大而 减小 ;在对称轴的 右边 ,曲线自左向右 上升 ,y随x的增大而 增大 .顶点是抛物线上位置最低的点,此时,函数y取得 最小值 ,是0.
②当a<0时,在对称轴 左边 ,曲线自左向右 上升 ,y随x的增大而 增大 ;在对称轴的右边,曲线自左向右 下降 ,y随x的增大而 减小 .顶点是抛物线上位置最高的点,此时,函数y取得最大值,是0.
【例6】在同一直角坐标系中y1=2x2,y2=-2x2和y3=x2的图像,正确的是下图的哪个选项( )
A. B. C. D.
【例7】已知函数是关于x的二次函数.(1)求m的值;(2)当m为何值时,该函数图像的开口向下;(3)当m为何值时该函数有最小值?试说明此时函数的增减性.
知识点五、二次函数y=ax2+c (a≠0)的图象和性质
1. 二次函数y=ax2+c (a≠0)的图象是一条抛物线,它的对称轴是y轴,顶点坐标(0,c),二次函数y=ax2 (a≠0)和y=ax2+c (a≠0)的图象 的形状相同,只是位置不同.y=ax2+c (a≠0)的图象可以看作是把y=ax2 (a≠0)的图象向上(c>0)或向下(c<0)平移个单位得到的.
2. 对于函数y=ax2+c (a≠0) 的增减性可简记如下:“抛物线开口向上,函数左减右增;抛物线开口向下,函数左增右减”.
【例8】已知点(-7,y1),(3,y2),(-1,y3)都在抛物线y=ax2+k(a>0)上,则( )
A. y1<y2<y3 B. y1<y3<y2 C. y3<y2<y1 D. y2<y1<y3
【习题精练】
1. 下列函数中,y是x的二次函数的是( )
A. x+y2+1=0 B. y=(x+1)(x-1)-x2 C. D. x2+y=0
2. 函数y=与y-kx2+k(k≠0)在同一直角坐标系中的图像可能是( )
A. B. C. D.
3. 小明在某次投篮中,球的运动路线是抛物线的一部分,如图所示,若球命中篮圈中心,则他与篮底的距离L是 m.
(3题)
4. 抛物线y=ax2+c (a≠0) 与抛物线y=-5x2的形状相同,开口方向一样,且顶点坐标为(0,3),则其所对应的函数表达式是什么?它是由抛物线y=-5x2怎样平移得到的?
5. 某广告公司设计一幅周长为12m的矩形广告牌,广告设计费为每平方米1000元,设矩形的一边长为x m,所花费用为y元。(1)请 你写 出y与x之间的函数关系式,写出x的取值范围;
6. 某商场销售一批名牌衬衫主,平均每天可售出20件,每件赢利40元。为了扩大销售,增加赢利,商场决定采取适当降价措施, 经调 查发现,如果每件衬衫降价1元,商场平均每天可多售出2件。若商场平均每天要赢利y元,每件衬衫降价x元,请你写出 y与x之间 的关系式。
7. 已知函数y=ax2(a≠0)与直线y=2x-3交于A(1,b)和点B,(1)求a和b的值;(2)求抛物线y=ax2的解析式,以及顶点坐标和对称轴;(3)x 为何值时,二次函数y=ax2中y随着x的增大而增大?(4)求S△ABO
(7题)
【提高训练】
☆8. 二次函数y=x2的图像如图,点0为坐标原点,点A在y轴的正半轴上,点B,C在二次函数y=x2的图像上,四边形OBAC为菱形,且∠OBA=120°,则菱形OBAC的面积为 m2.
(8题)
☆9. 如图所示,已知ΔABC是一个等腰三角形铁板余料,其中AB=AC=20cm,BC=24cm,若在ΔABC上截出一个矩形零件DEFG,使EF在边BC上,点D、G分别在边AB、AC上,设DE=x cm,S矩形DEFG=y cm2,你能写出y与x之间的函数关系式吗?
(9题)
【培优训练】
☆☆10. 某宾馆有50个房间供游客住宿,当每个房间的房价为每天180元时,房间会全部住满.当每个房间每天的房价每增加10元时,就会有一个房间空闲.宾馆需对游客居住的每个房间每天支出20元的各种费用.根据规定,每个房间每天的房价不得高于340元.设每个房间的房价每天增加x元(x为10的正整数倍).(1)设一天订住的房间数为y,直接写出y与x的函数关系式及自变量x的取值范围;(2)设宾馆一天的利润为W元,求W与x的函数关系式.
九(下)第二章 二次函数(第十四周周末教案 课时28)
第二节 二次函数的图像和性质
知识点一、二次函数y=a(x-h)2和y=a(x-h)2+k的图象和性质
1. 二次函数y=a(x-h)2是由抛物线y=ax2向左或向右平移个单位得到;h>0时,向右平移;h<0时,向左平移.对称轴是直线x=h,顶点坐 标是(h,0)。
2. 二次函数y=a(x-h)2+k 的图象可由抛物线y=ax2 平移得到,把y=ax2的图象先向左或右平移个单位,得到y=a(x-h)2的图象,再向上或 向下平移个单位,顶点坐标是(h,k),对称轴是直线x=h。
点拨:二次函数y=a(x-h)2和y=a(x-h)2+k,都说当完全平方项(x-h)2=0,即x=h时,y有最值。
【例1】将函数y=的图像向左平移1个单位,再向下平移2个单位,此时函数图像对应的解析式为( )
A. B. C. D.
【例2】对于抛物线y=(x-1)2-2,下列说法错误的是( )
A. 顶点坐标是(1,-2) B. 对称轴是直线x=1 C. 开口方向向上 D. 当x>1时,y随x的增大而减小
知识点二、二次函数一般式y=ax2+bx+c (a≠0)的图象和性质
1. 二次函数的一般式 y=ax2+bx+c (a≠0) 与顶点式y=a(x-h)2+k可互相转化.
(1)通过去括号、合并同类项可将顶点式化为一般式;
(2)利用配方法可将一般式化为顶点式:y=ax2+bx+c可化为
2.二次函数y=ax2+bx+c (a≠0)的图象是一条抛物线,它的对称轴是直线x=,顶点坐标是(,).
点拨
3. 二次函数y=ax2+bx+c (a≠0)的图象特征与a、b、c的符号之间的关系
【例3】抛物线的开口向 ,顶点坐标为 ,对称轴是直线 。
【例4】二次函数y=ax2+bx+c的图象如图所示,则下列判断中错误的是( )
A. 图象的对称轴是直线x=1 B. 当x>1时,y随x的增大而减小
C. abc<0 D. 当-1<x<3时,y<0
(例4)
【例5】如图为抛物线y=ax2+bx+c的图象,A,B,C为抛物线与坐标轴的交点,且OA=OC=1,则下列关系正确的是( )
A. a+b=-1 B. a-b=-1 C. b<2a D. ac<0
(例5)
第三节 确定二次函数的表达式
知识点三、用待定系数法求二次函数的表达式
1. 二次函数表达式的三种形式:
特别地:
注意:把顶点坐标代入顶点式y=a(x-h)2+k 时,要注意h与k的符号.
2. 用待定系数法求函数表达式的一般步骤:
【例6】已知二次函数对称轴为x=2,且在x轴上截得的线段长为6,与y轴交点为(0,-2),则此二次函数的解析式为
【例7】已知抛物线经过两点A(1,0),B(0,-3),且对称轴是直线x=2,求此抛物线的解析式.
【例8】在直角坐标平面内,抛物线y=ax2+bx+c经过原点O、A(-2,-2)与B(1,-5)三点.(1)求抛物线的表达式;(2)写出该抛物线的顶点坐标.
【习题精练】
1. 二次函数y=ax2的图像向左平移2个单位,向下平移3个单位,所得新函数表达式为( )
A. y=a(x-2)2+3 B. y=a(x-2)2-3 C. y=a(x+2)2+3 D. y=a(x+2)2-3
2. 把二次函数用配方法化成y=a(x-h)2+k的形式是( )
A. B. C. D.
3. 若二次函数(a,b为常数)的图象如图,则a的值为( )A. 1 B. C. D. -2
(3题)
4. 如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0;②2a+b=0;③a+b+c>0;④当-1<x<3时,y>0。其中正确的个数为( )A. 1 B. 2 C. 3 D.4
(4题)
5. 抛物线y=2x2+bx+c的顶点坐标是(1,-2),则b= ,c= .
6. 二次函数的图象与x轴的两个交点(-2,0),(4,0),且过点(1,9),则解析式为 .
7. 已知二次函数y=ax2+bx+c的图象如图所示,则点P(a,bc)在 .
(7题)
8.已知二次函数的图象经过(0,0)、(1,-1)、(-2,14)三点,求这个二次函数的解析式及顶点坐标;
【提高训练】
☆9. 如图,已知二次函数y=x2+bx+c的图象经过点(-1,0),(1,-2),当y随x的增大而增大时,x的取值范围是 .
(9题)
☆10. 设A(-2,y1),B(1,y2),C(2,y3)是抛物线y=-(x+1)2+a上的三点,则y1,y2,y3的大小关系为
☆11. 如图,抛物线的顶点为P(﹣2,2),与y轴交于点A(0,3). 若平移该抛物线使其顶点P沿直线移动到点P′(2,﹣2),点A的对应点为A′, 则抛物线上PA段扫过的区域(阴影部分)的面积为 .
(11题)
【培优训练】
☆☆12. 已知二次函数y=ax2+bx+c(a≠0)的图像如图所示,有下列5个结论:①abc>0; ②b
(12题)
九(下)第二章 二次函数第1~3节(第十四周 强化训练14)
【习题精练】
1.已知二次函数y1=﹣3x2,,它们的图象开口由小到大的顺序是( )
A. y1<y2<y3 B. y3<y2<y1 C. y1<y3<y2 D. y2<y3<y1
2. 已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,则下列结论中,正确的是( )
A. a>0 B. b<0 C. c<0 D. a+b+c>0
(2题)
3. 如图,抛物线y=ax2+bx+c(a≠0)的图象与x轴的一个交点是(-2,0),顶点是(1,3).下列说法中不正确的是( )
A.抛物线的对称轴是x=1 B.抛物线的开口向下
C.抛物线与x轴的另一个交点是(2,0) D.当x=1时,y有最大值是3
(3题)
4. 已知二次函数y=a(x+1)2-b(a≠0)有最小值1,则a,b的大小关系为( )
A.a>b B.a<b C.a=b D.不能确定
5. 函数y=ax+b和y=ax2+bx+c在同一直角坐标系内的图象大致是( )
A. B. C. D.
6. 把x2﹣4x+1化成(x﹣h)2+k其中h,k是常数)形式的结果为( )
A. (x﹣2)2﹣3 B. (x﹣4)2﹣15 C. (x﹣2)2+3 D. (x﹣4)2+15
7. 已知二次函数y=x2-6x+m的最小值为1,那么m的值是 .
8. 如图, 抛物线y=ax2+3与y轴交于点A,过点A与x轴平行的直线交抛物线于点B、C,则BC的长为 .
(8题)
9. 若抛物线y=ax2+c的形状与y=2x2的相同,开口方向相反,且其顶点坐标是(0,-3),则该抛物线的函数表达式是 .
10. 将抛物线y=3x2向上平移3个单位,再向左平移2个单位,那么得到的抛物线的解析式为 .
11.如图,二次函数y=ax2+bx+c的图象经过点(-1,0)、(3,0)和(0,2),当x=2时,y的值为多少?.
(11题)
【提高训练】
12. 下列图形中阴影部分的面积相等的有( )A. ①② B. ②③ C. ③④ D. ①④
13. 如图,抛物线经过平移得到抛物线,其对称轴与两段抛物线所围成的阴影部分的面积为 .
(13题)
14 松花江大桥的一个桥拱为抛物线的形状,拱顶A离桥面50m,桥面上拱形钢梁之间距离BC=120m,建立如图所示的直角坐标系。(1) 写出A,B,C三点的坐标;(2)求该抛物线的解析式。
(14题)
15. 在直角坐标平面中,O为坐标原点.二次函数y=x2+bx+c的图象与x轴的负半轴相交于点A,与x轴的正半轴相交于点B,与y轴交 于点C(如图所示).点C的坐标为(0,-3),且BO=CO.(1)求这个二次函数的解析式;(2)设这个二次函数图象的顶点 为M,求AM的长.
(15题)
【培优训练】
16. 已知二次函数的图象如图所示对称轴为.下列结论中,正确的是( )
A. B. C. D.
(16题)
17. 如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A(-1,0)和点B(0,-5).(1)求该二次函数的解析式;(2)根据图象,写出函数值y 为正数时,自变量x的取值范围.(3)已知该函数图象的对称轴上存在一点P,使得△ABP的周长最小.请求出点P的坐标.
(17题)
北师大版九年级上册数学:第19周末教案+强化(学生版): 这是一份北师大版九年级上册数学:第19周末教案+强化(学生版),共6页。
北师大版九年级上册数学:第18周末教案+强化(学生版): 这是一份北师大版九年级上册数学:第18周末教案+强化(学生版),共8页。
北师大版九年级上册数学:第17周末教案+强化(学生版): 这是一份北师大版九年级上册数学:第17周末教案+强化(学生版),共9页。













