北师大版九年级数学上册 第六章反比例函数复习课件

这是一份北师大版九年级数学上册 第六章反比例函数复习课件，共19页。PPT课件主要包含了本章知识结构图，二重点知识，考点整合训练，反比例，双曲线，x≠0，用描点法，y3＞y1＞y2，y-6x，课堂小结等内容，欢迎下载使用。

  复习目标：  （1）巩固反比例函数的概念，会求反比例函数表达式并能画出图象． （2）巩固反比例函数图象的变化其及性质并能运用解决某些实际问题．
复习重点、难点：重点：反比例函数的定义、图像性质。   难点：反比例函数增减性的理解。
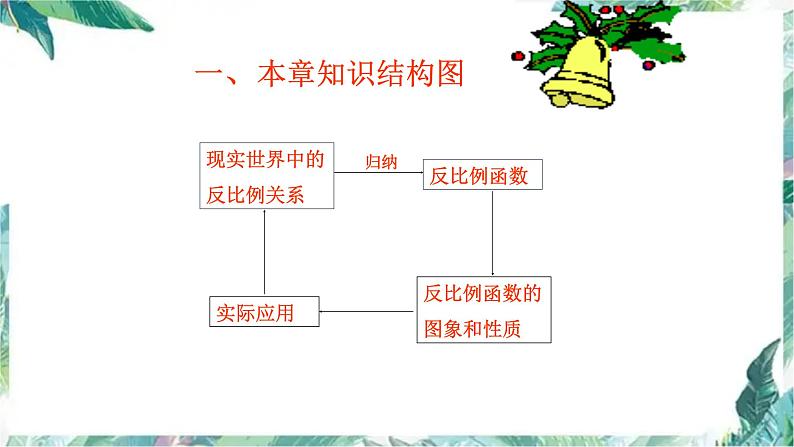
现实世界中的反比例关系
反比例函数的图象和性质
若 为反比例函数,则m= __
注意：①列表时自变量取值要均匀和对称,x≠0②连线时自左往右用光滑曲线顺次连结，切忌用折线。③两个分支合起来才是反比例函数图象。
考点2：反比例函数的图像与性质
3、用描点法
4.函数 的图象位于第 象限, 在每一象限内,y的值随x的增大而 , 当x＞0时,y 0,这部分图象位于第 象限.
由1－3m＜0 得－3m＜－ 1
方法1 用图像法解
方法2 用求值法解
∵当x1=-2时， y1=-2当x2=-1 时，y2=-4当x3=4时 ，y3=1 ∴ y3＞ y1 ＞y2
考点3：反比例函数与正比例函数 的关系
在每一个象限内:当k>0时，y随x的增大而减小;当k<0时，y随x的增大而增大.
y=kx(k≠0)( 特殊的一次函数)
当k>0时，y随x的增大而增大;当k<0时，y随x的增大而减小.
7.已知函数y=k/x 的图象如下右图，则y=k x-2 的图象大致是（　）
8.如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的关系式是 .
考点4：反比例函数的几何意义
（变式练习）一个反比例函数的图象在第二象限，如图，点A是图象上任意一点，AM⊥x轴于点M，O是原点，如果△AOM的面积为3，则这个反比例函数的解析式是 。
9。已知反比例函数y =k/x 和一次函数 y=kx+b的图象都经过点（2，1）（1）分别求出这个函数的解析式
考点5：反比例函数与一次函数的综合运用
解：（1）∵反比例函数y=k/x的图像经过点（2，1） ∴1=k/2，即k=2 ∴反比例函数的解析式为y=2/x 又∵一次函数y=kx+b和反比例函数y=k/x的k值相等，且也经过点（2，1） 解得k=2,b=－3 ∴一次函数的解析式为y=2x －3
解：（2）当x= －2时，反比例函数的函数值y= －1；一次函数的函数值y= －7 ∴点A（ －2，－1）在反比例函数的图像上。
（2）试判断是A（-2， -1）在哪个函数的图象上
请大家围绕以下几个问题小结本课内容：
1、反比例函数的图象是什么样子的？ 它与正比例函数的图象有什么不同？
2、反比例函数的性质是什么？ 它与正比例函数有什么共同点和不同点？
3、在本节课练习中你运用了哪些数学思想和方法？
1、函数 的图象在第________象限, 在每一象限内，y 随x 的增大而_________.2、函数 的图象在第________象限, 在每一象限内，y 随x 的增大而_________.3、函数 ,当x>0时,图象在第____象限, y随x 的增大而_________.
如图，一次函数与反比例函数的图象相交于A、B两点，则图中使反比例函数的值小于一次函数的值的x的取值范围是（　　）．
A、x＜－1　　　　　 B、x＞2C、－1＜x＜0或x＞2　D、x＜－1或0＜x＜2