人教版九年级上册数学活动多媒体教学ppt课件

这是一份人教版九年级上册数学活动多媒体教学ppt课件，共25页。PPT课件主要包含了导入课题，活动目标，活动1，三角形点阵，活动2，正六边形点阵，①填写下表，n-1，n+3，n+2等内容，欢迎下载使用。
点是几何中最基本的图形，许多点排列起来可以组成一个点阵.
今天我们就来看看点阵中隐藏了什么有趣的数学规律.
1.导入课题：老师在黑板上画1个点，说明点是几何中最基本的图形，许多点排列起来可以构成一个点阵,点阵是非常有趣的图形.今天我们就来研究“点阵中的规律”.(板书课题)
(1)通过观察点阵（数学模型），了解并掌握一些点阵及数学模型的变化规律. (2)探究三角点阵中前n行的点数和的计算公式. (3)运用一元二次方程的知识和三角点阵中前n行的点数和的计算公式解决问题. (4)通过活动，培养学生的观察、比较、归纳和概括能力,培养学生的空间想象能力.
图1是一个三角形点阵，从上向下数有无数多行，其中第一行有1个点，第二行有2个点……第n行有n个点…….观察图形，完成下面各题.
····························……
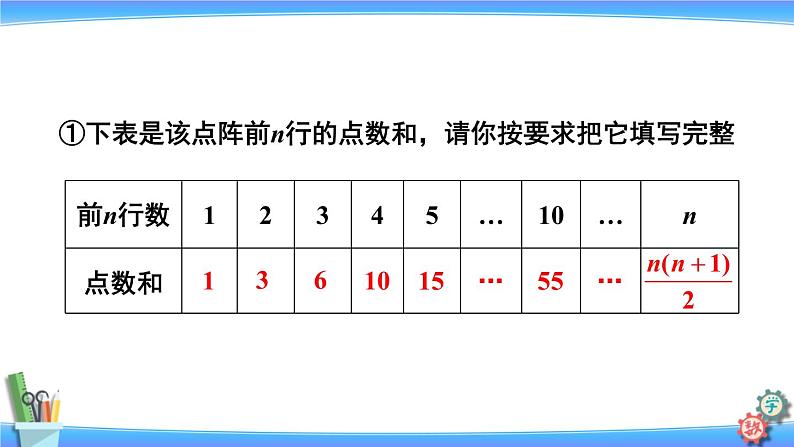
①下表是该点阵前n行的点数和，请你按要求把它填写完整
②若该三角点阵前n行的点数和是300，求行数n.
由①知.前n行的点数和为 ，解得n1=24，n2=-25(舍去)，即行数n为24.
③该三角点阵前n行的点数和能是600吗？如果能，求出其行数n；如果不能，请说明理由.
前n行的点数和 ,解得n1= , n2= ,因为n是正整数，方程的两根均不符合条件，所以三角点阵前n行的点数和不能是600.
④如果把图中的三角点阵中各行的点数依次换为2，4，6，…，2n，…，你能探究出前n行的点数和满足什么规律吗？
⑤在④中，三角点阵中前n行的点数和能是600吗？如果能，求出n；如果不能，试用一元二次方程说明理由.
依题意，n(n+1)=600.解得n1=24，n2=-25(舍去).
如图2 是一个形如正六边形的点阵，它的中心是一个点，算作第一层，第二层每边有两个点，第三层每边有三个点，……，依此类推.
②第n层所对应的点数为 （n≥2）.
③写出n层正六边形点阵的总点数（n≥2）；
1+6×1+6×2+…+6(n-1)=1+6·=1+3n(n-1)
④如果点阵中所有层的总点数为331，请求出它共有几层？
1+3n(n-1)=331化简方程为：n2-n-110=0分解因式为：(n-11)(n+10)=0 解得：n1=11，n2=-10(舍去)， 所以共有11层.
⑤ 点阵设计大赛： 设计时间：5分钟. 设计要求： a .每人设计一组有规律、美观的点阵图，画出前4个点阵，并仿照三角形点阵的探究提出问题，然后在小组内交流自己的设计方案. b.每组评选出优秀作品，派代表说明设计的方法及点阵中的规律.
1. 古希腊著名的毕达哥拉斯学派把1，3，6，10…这样的数称为“三角形数”，而把1，4，9，16…这样的数称为“正方形数”.观察下面的点阵图和相应的等式，探究其中的规律.（1）下图反映了一个“三角形数”是如何得到的，认真观察，并在④后面的横线上写出相应的等式；
①1=1；②1+2= ；③1+2+3= ；④1+2+3+4= .
（2）通过猜想，写出（1）中与第九个点阵相对应的等式： 。 （3）2015是“三角形数”吗？为什么？
1+2+3+…+9=45
解：不是.“三角形数”都可以写成 的形式， 令2015= ， 解得n1= ，n2= . 因为n是正整数，方程的两根均不符合条件，所以2015不是“三角形”数.
（4）从下图中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和. 结合（1）观察下列点阵图，并在⑤后面的横线上写出相应的等式.
①1=12； ②1+3=22；③3+6=32； ④6+10=42；⑤ .
（5）通过猜想，写出（4）中与第n个点阵相对应的等式： .
（6）判断225是不是“正方形数”，如果不是，说明理由；如果是，225可以看作哪两个相邻的“三角形数”之和？
解：是. ∵152=225. ∴225是“正方形数”. 由(5)得， ，∴225可以看作105，120这两个相邻的“三角形数”之和.
2.如图，用同样规格黑白两色的正方形瓷砖铺设矩形地面.请观察下列图形并解答有关问题： (1)在第n个图中，每一横行共有 块瓷砖，每一竖列共有 块瓷砖(均用含n的代数式表示)；
(2) 按上述铺设方案，铺一块这样的矩形地面共用了506块瓷砖，求此时n的值；
解：(2)第n个图共有(n2+5n+6)块瓷砖. 由n2+5n+6=506. 解得n1=20,n2=-25(舍去).∴n=20.
(3) 若黑瓷砖每块4元，白瓷砖每块3元，在问题(2)中，共需花多少元钱购买瓷砖?
白瓷砖块数是n(n+1)=20×(20+1)=420,黑瓷砖块数是506-420=86.86×4+420×3=1604(元).共需1604元钱购买瓷砖.
(4) 是否存在黑瓷砖与白瓷砖块数相等的情形?请通过计算说明为什么?
在第n个图中白瓷砖块数是n(n+1).则有n(n+1)=(n2+5n+6)-n(n+1)化简得n2-3n-6=0解得n1= , n2= .∵n为正整数，不合题意.∴不存在黑瓷砖与白瓷砖块数相等的情形.
三角形点阵前n行数点数和
正六边形第n层所对应的点数（n≥2）
n层正六边形点阵的总点数（n≥2）；