专题8 函数模型及其应用（讲义）-2023年高考一轮复习精讲精练必备

这是一份专题8 函数模型及其应用（讲义）-2023年高考一轮复习精讲精练必备，文件包含第8讲函数模型及其应用解析-2023年高考一轮复习精讲精练必备docx、第8讲函数模型及其应用讲义-2023年高考一轮复习精讲精练必备docx等2份试卷配套教学资源，其中试卷共18页， 欢迎下载使用。
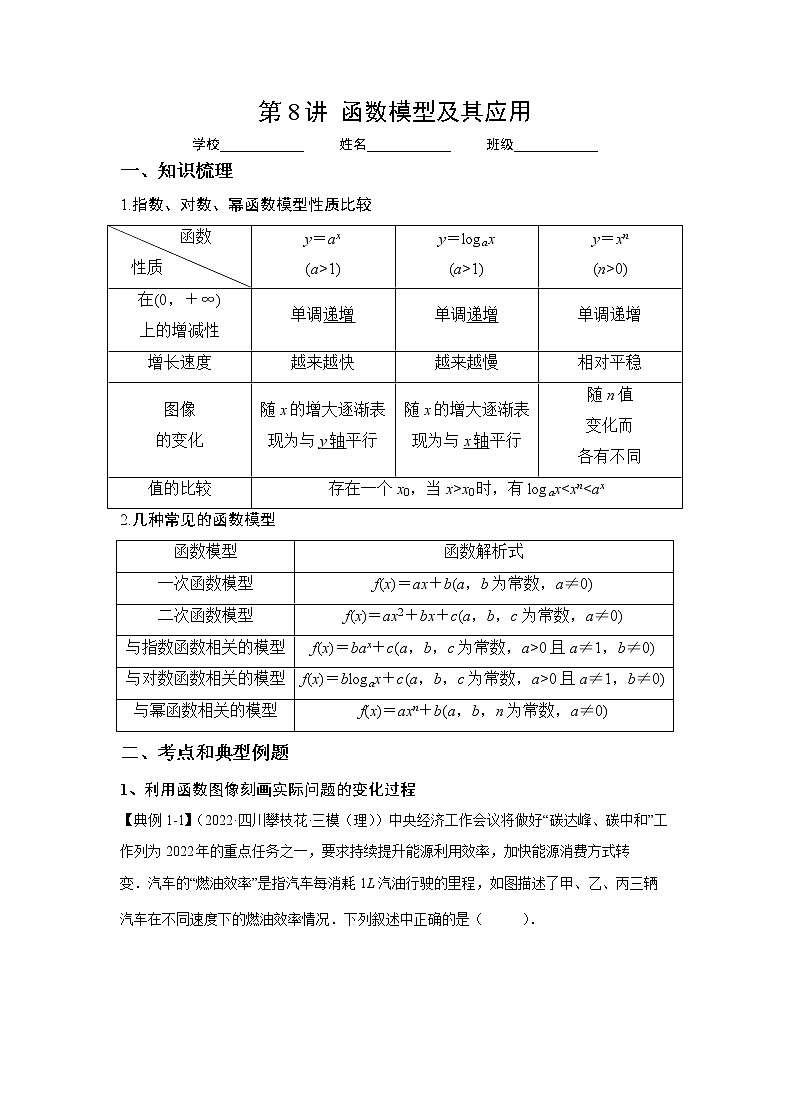
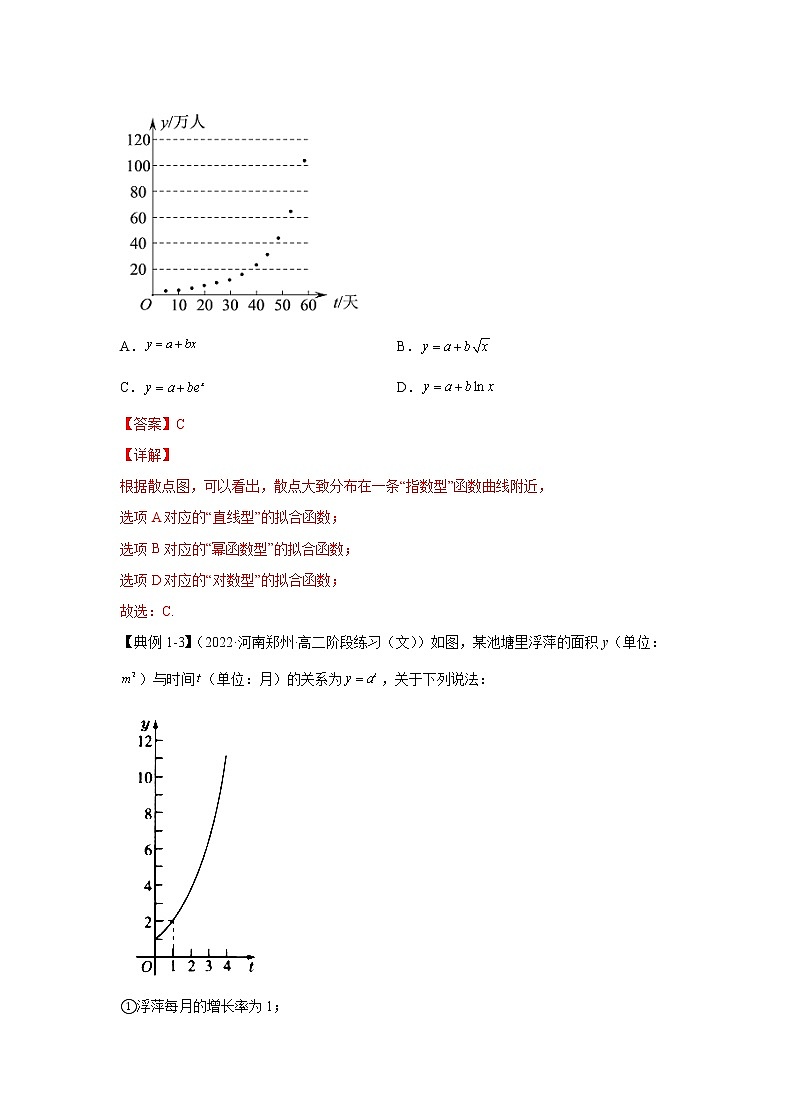
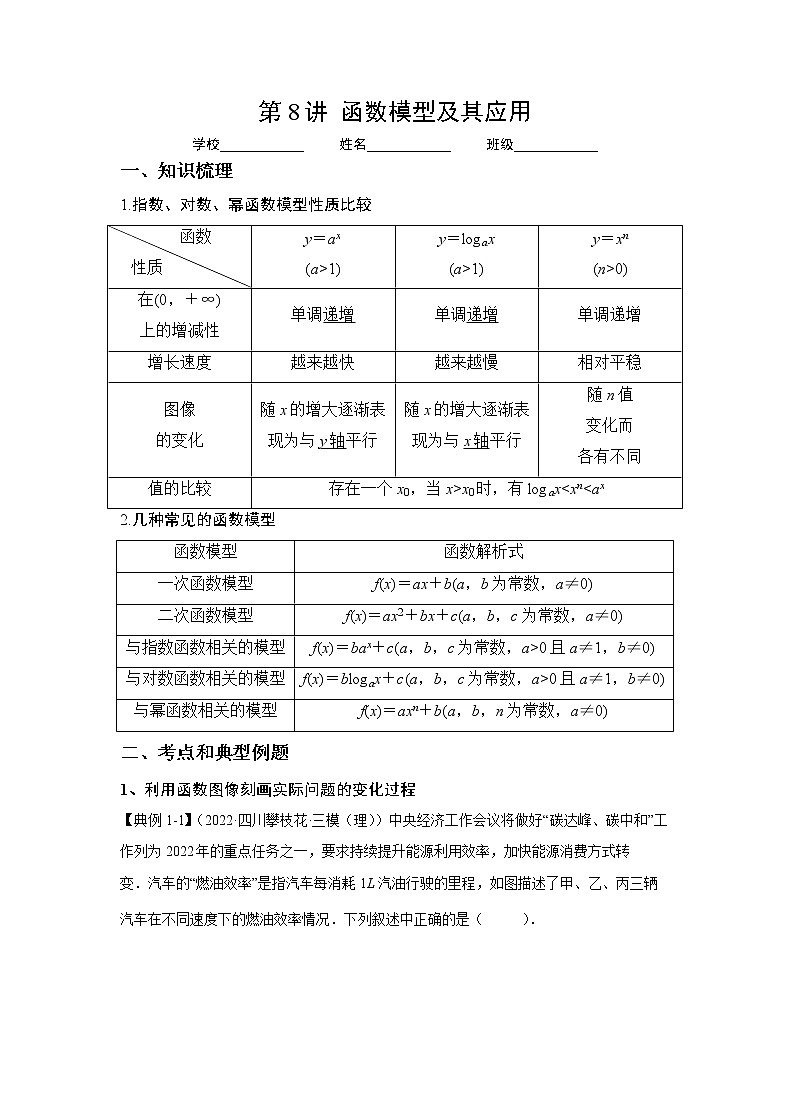
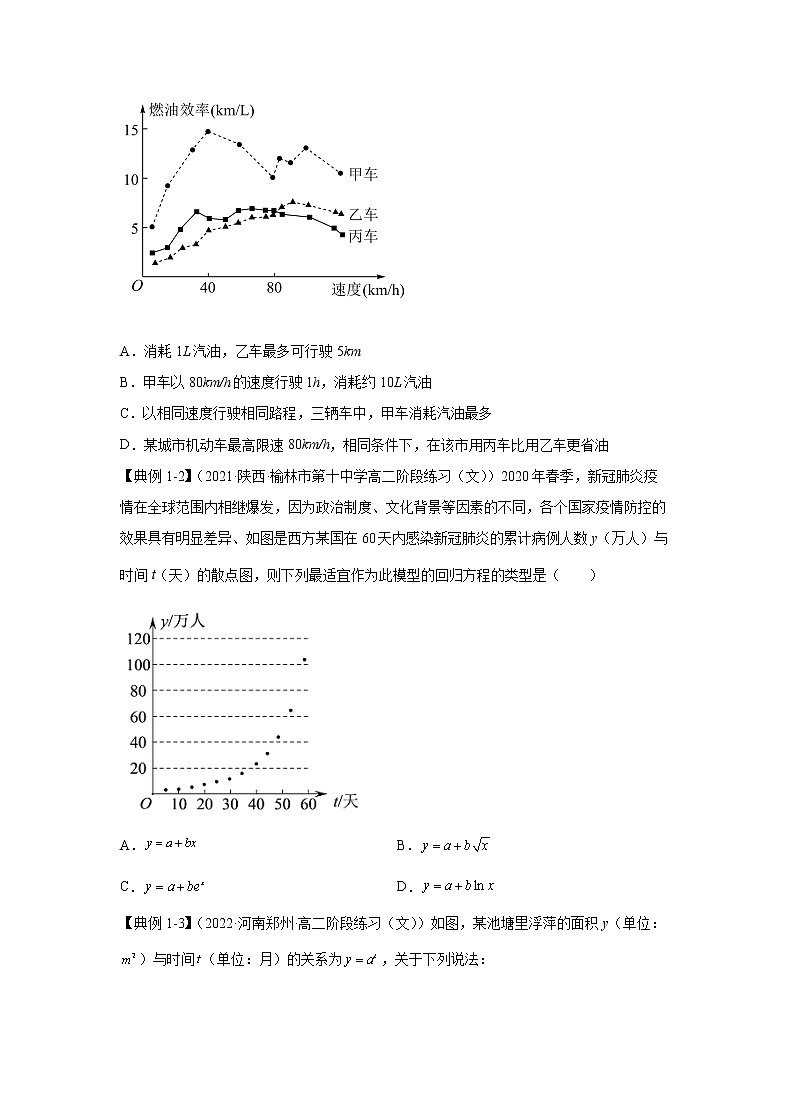
第8讲  函数模型及其应用学校____________          姓名____________          班级____________ 一、知识梳理1.指数、对数、幂函数模型性质比较　　函数性质　　　y＝ax(a>1)y＝logax(a>1)y＝xn(n>0)在(0，＋∞)上的增减性单调递增单调递增单调递增增长速度越来越快越来越慢相对平稳图像的变化随x的增大逐渐表现为与y轴平行随x的增大逐渐表现为与x轴平行随n值变化而各有不同值的比较存在一个x0，当x>x0时，有logax<xn<ax2.几种常见的函数模型函数模型函数解析式一次函数模型f(x)＝ax＋b(a，b为常数，a≠0)二次函数模型f(x)＝ax2＋bx＋c(a，b，c为常数，a≠0)与指数函数相关的模型f(x)＝bax＋c(a，b，c为常数，a>0且a≠1，b≠0)与对数函数相关的模型f(x)＝blogax＋c(a，b，c为常数，a>0且a≠1，b≠0)与幂函数相关的模型f(x)＝axn＋b(a，b，n为常数，a≠0)二、考点和典型例题1、利用函数图像刻画实际问题的变化过程【典例1-1】（2022·四川攀枝花·三模（理））中央经济工作会议将做好“碳达峰、碳中和”工作列为2022年的重点任务之一，要求持续提升能源利用效率，加快能源消费方式转变．汽车的“燃油效率”是指汽车每消耗1L汽油行驶的里程，如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况．下列叙述中正确的是（       ）． A．消耗1L汽油，乙车最多可行驶5kmB．甲车以80km/h的速度行驶1h，消耗约10L汽油C．以相同速度行驶相同路程，三辆车中，甲车消耗汽油最多D．某城市机动车最高限速80km/h，相同条件下，在该市用丙车比用乙车更省油【答案】D【详解】对于A：当乙车速度大于时，乙车车每消耗1L汽油行驶的里程都超过了，所以A错误；对于B：甲车以80km/h的速度行驶时，燃油效率为，则行驶1h消耗约8L汽油，所以B错误；对于C：以相同速度行驶相同路程，燃油效率越高耗油越少，故三辆车中，甲车消耗汽油最少，所以C错误；对于D：机动车最高限速80km/h相同条件下，丙车比乙车燃油效率高，故更省油，所以D正确.故选：D.【典例1-2】（2021·陕西·榆林市第十中学高二阶段练习（文））2020年春季，新冠肺炎疫情在全球范围内相继爆发，因为政治制度、文化背景等因素的不同，各个国家疫情防控的效果具有明显差异、如图是西方某国在60天内感染新冠肺炎的累计病例人数y（万人）与时间t（天）的散点图，则下列最适宜作为此模型的回归方程的类型是（     ）A． B．C． D．【答案】C【详解】根据散点图，可以看出，散点大致分布在一条“指数型”函数曲线附近，选项A对应的“直线型”的拟合函数；选项B对应的“幂函数型”的拟合函数；选项D对应的“对数型”的拟合函数；故选：C.【典例1-3】（2022·河南郑州·高二阶段练习（文））如图，某池塘里浮萍的面积y（单位：）与时间（单位：月）的关系为，关于下列说法：①浮萍每月的增长率为1；②第5个月时，浮萍面积就会超过；③浮萍每月增加的面积都相等；④若浮萍蔓延到所经过的时间分别是，则，其中正确的说法是（       ）A．①② B．①②③ C．①②④ D．①②③④【答案】C【详解】因为图像过，所以由，所以，故原题中函数关系为对于①：，所以每个月的增长率为1，故①正确；对于②：当时，，故②正确；对于③：第二个月比第一个月增加第三个月比第二个月增加，故③错误；对于④：由题，所以，所以，故④正确；故选：C【典例1-4】（2022·新疆吐鲁番·高一期末）如图，某池塘里浮萍的面积（单位：）与时间t（单位：月）的关系为，关于下列说法不正确的是（       ）A．浮萍每月的增长率为2B．浮萍每月增加的面积都相等C．第4个月时，浮萍面积超过D．若浮萍蔓延到所经过的时间分别是，、，则【答案】B【详解】解：图象可知，函数过点，，函数解析式为，浮萍每月的增长率为，故选项A正确，函数是指数函数，是曲线型函数，浮萍每月增加的面积不相等，故选项B错误，当时，，故选项C正确，对于D选项，，，，，又，，故选项D正确，故选：B．2、已知函数模型解决实际问题【典例2-1】（2022·重庆南开中学模拟预测）浮萍是我国南方常见的一种水生植物，生长速度非常快．最快每30个小时浮萍铺在水面的面积就可以扩大为原来的2倍．李大爷承包了一块面积为3亩（1亩≈666.7平方米）的鱼塘，为养殖草鱼购买了一些浮萍．最初，浮萍铺在水面上大约有1平方米，如果浮萍始终以最高效繁殖，大约（       ）天后，浮萍可以铺满整个鱼塘．（不考虑草鱼对浮萍的损耗．结果四舍五入到整数，参考数据：）A．12 B．14 C．16 D．18【答案】B【详解】由题，鱼塘面积共平方米，浮萍天后在水面上的面积大约有平方米，故浮萍铺满整个鱼塘的天数满足，两边取对数化简有，解得，故大约14天后，浮萍可以铺满整个鱼塘故选：B【典例2-2】（2022·辽宁葫芦岛·一模）某高中综合实践兴趣小组做一项关于某水果酿制成醋的课题研究．经大量实验和反复论证得出，某水果可以酿成醋的成功指数M与该品种水果中氢离子的浓度N有关，酿醋成功指数M与浓度N满足．已知该兴趣小组同学通过数据分析估计出某水果酿醋成功指数为2.9，则该水果中氢离子的浓度约为（）（       ）A．0.2 B．0.4 C．0.6 D．0.8【答案】D【详解】由题意知：，整理得，解得，又，故.故选：D.【典例2-3】（2022·广西·模拟预测（理））异速生长规律描述生物的体重与其它生理属性之间的非线性数量关系通常以幂函数形式表示．比如，某类动物的新陈代谢率与其体重满足，其中和为正常数，该类动物某一个体在生长发育过程中，其体重增长到初始状态的16倍时，其新陈代谢率仅提高到初始状态的8倍，则为（       ）A． B． C． D．【答案】D【详解】设初始状态为，则，，又，，即，，，，，．故选：D．【典例2-4】（2022·重庆·模拟预测）我国的酒驾标准是指车辆驾驶员血液中的酒精含量大于或者等于，已知一驾驶员某次饮酒后体内每血液中的酒精含量（单位：）与时间（单位：）的关系是：当时，；当时，，那么该驾驶员在饮酒后至少要经过__________才可驾车.【答案】【详解】当时，，当时，函数有最大值，所以当时，饮酒后体内每血液中的酒精含量小于，当当时，函数单调递减，令，因此饮酒后小时体内每血液中的酒精含量等于，故答案为：【典例2-5】（2022·北京西城·一模）调查显示，垃圾分类投放可以带来约元/千克的经济效益.为激励居民垃圾分类，某市准备给每个家庭发放一张积分卡，每分类投放积分分，若一个家庭一个月内垃圾分类投放总量不低于，则额外奖励分（为正整数）.月底积分会按照元/分进行自动兑换.①当时，若某家庭某月产生生活垃圾，该家庭该月积分卡能兑换_____元；②为了保证每个家庭每月积分卡兑换的金额均不超过当月垃圾分类投放带来的收益的%，则的最大值为___________.【答案】          【详解】①若某家庭某月产生生活垃圾，则该家庭月底的积分为分，故该家庭该月积分卡能兑换元；②设每个家庭每月产生的垃圾为，每个家庭月底月积分卡能兑换的金额为元.若时，恒成立；若时，，可得.故的最大值为.故答案为：①；②. 3、构造函数模型解决实际问题【典例3-1】（2022·广东茂名·二模）双碳，即碳达峰与碳中和的简称，2020年9月中国明确提出2030年实现“碳达峰”，2060年实现“碳中和”．为了实现这一目标，中国加大了电动汽车的研究与推广，到2060年，纯电动汽车在整体汽车中的渗透率有望超过70%，新型动力电池随之也迎来了蓬勃发展的机遇．Peukert于1898年提出蓄电池的容量C（单位：A·h），放电时间t（单位：h）与放电电流I（单位：A）之间关系的经验公式，其中为Peukert常数．在电池容量不变的条件下，当放电电流时，放电时间，则当放电电流，放电时间为（       ）A．28h B．28.5h C．29h D．29.5h【答案】B【详解】解：根据题意可得，则当时，，所以，即当放电电流，放电时间为28.5h.故选：B.【典例3-2】（2022·天津市第七中学模拟预测）一种药在病人血液中的量不少于才有效，而低于病人就有危险．现给某病人注射了这种药，如果药在血液中以每小时的比例衰减，为了充分发挥药物的利用价值，那么从现在起经过 （       ）小时向病人的血液补充这种药，才能保持疗效．（附：，，结果精确到）A．小时 B．小时 C．小时 D．小时【答案】A【详解】设应在病人注射这种药小时后再向病人的血液补充这种药，则，整理可得：，，，，，即应在用药小时后再向病人的血液补充这种药.故选：A.【典例3-3】（2022·福建龙岩·模拟预测）进入4月份以来，为了支援上海抗击疫情，A地组织物流企业的汽车运输队从高速公路向上海运送抗疫物资.已知A地距离上海500，设车队从A地匀速行驶到上海，高速公路限速为.已知车队每小时运输成本（以元为单位）由可变部分和固定部分组成，可变部分与速度v的立方成正比，比例系数为b，固定部分为a元.若，，为了使全程运输成本最低，车队速度v应为（       ）A．80 B．90 C．100 D．110【答案】C【详解】解：设运输成本为元，依题意可得，则所以当时，当时，当时，即函数在上单调递减，在上单调递增，所以当时取得极小值即最小值，所以时全程运输成本最低；故选：C【典例3-4】（2022·贵州毕节·三模（理））20世纪70年代，里克特制订了一种表明地震能量大小的尺度，就是使用测震仪衡量地震能量的等级，地震能量越大，测震仪记录的地震曲线的振幅就越大，这就是我们常说的里氏震级，其计算公式为，其中是被测地震的最大振幅，是“标准地震”的振幅．假设在一次地震中，一个距离震中千米的测震仪记录的地震最大振幅是，此时标准地震的振幅是，计算这次地震的震级为（       ）A． B． C． D．【答案】B【详解】依题意知，因此，这次地震的震级约为里氏级.故选：B.【典例3-5】（2022·安徽·南陵中学模拟预测（理））充电电池是电动汽车的核心部件之一，如何提高充电速度是电池制造商重点关注的研究方向已知电池充入的电量E（单位：）与充电时间t（单位：）满足函数，其中M表示电池的容量，k表示电池的充电效率，研究人员对A，B两个型号的电池进行充电测试，电池A的容量为，充电充入了的电量；电池B的容量为，充电充入了的电量.设电池A的充电效率为，电池B的充电效率为，则（       ）A． B． C． D．大小关系无法确定【答案】B【详解】由题意得，则， 同理，则，得，由指数函数单调性得，即．故选：B