高考数学一轮复习第3章三角函数解三角形第6讲解三角形学案

这是一份高考数学一轮复习第3章三角函数解三角形第6讲解三角形学案，共17页。
知识梳理·双基自测
eq \x(知)eq \x(识)eq \x(梳)eq \x(理)
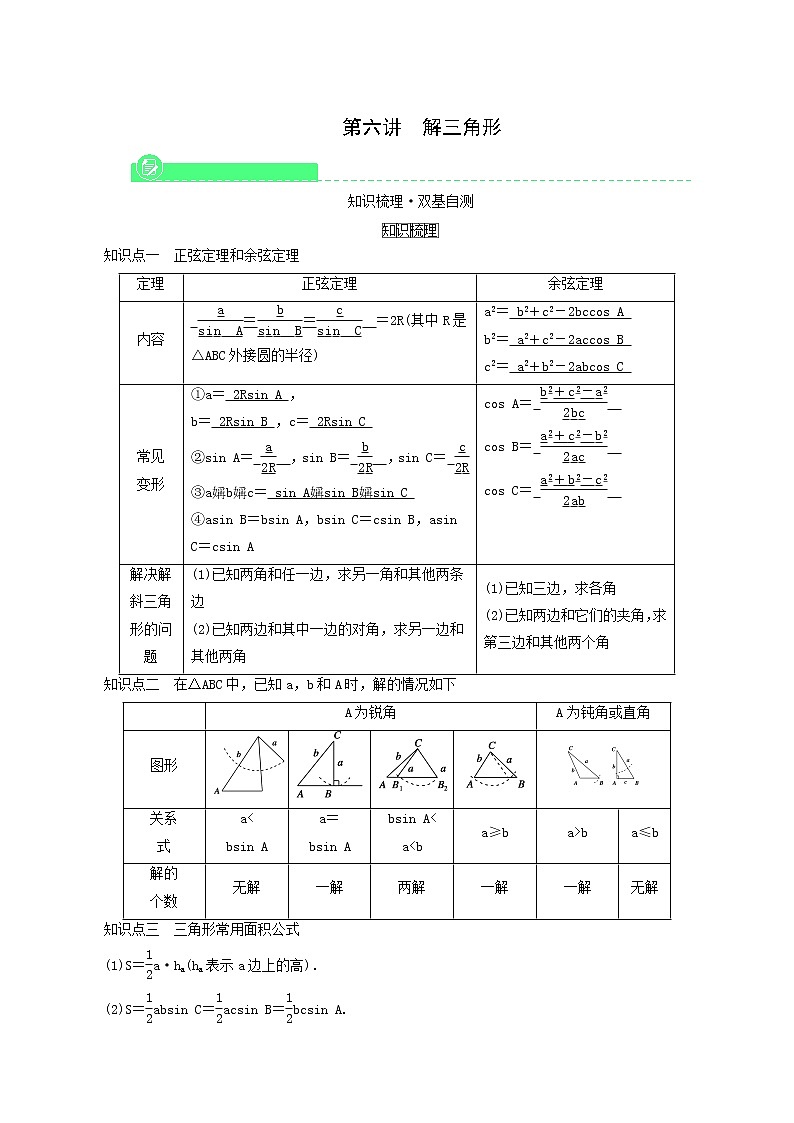
知识点一 正弦定理和余弦定理
知识点二 在△ABC中，已知a，b和A时，解的情况如下
知识点三 三角形常用面积公式
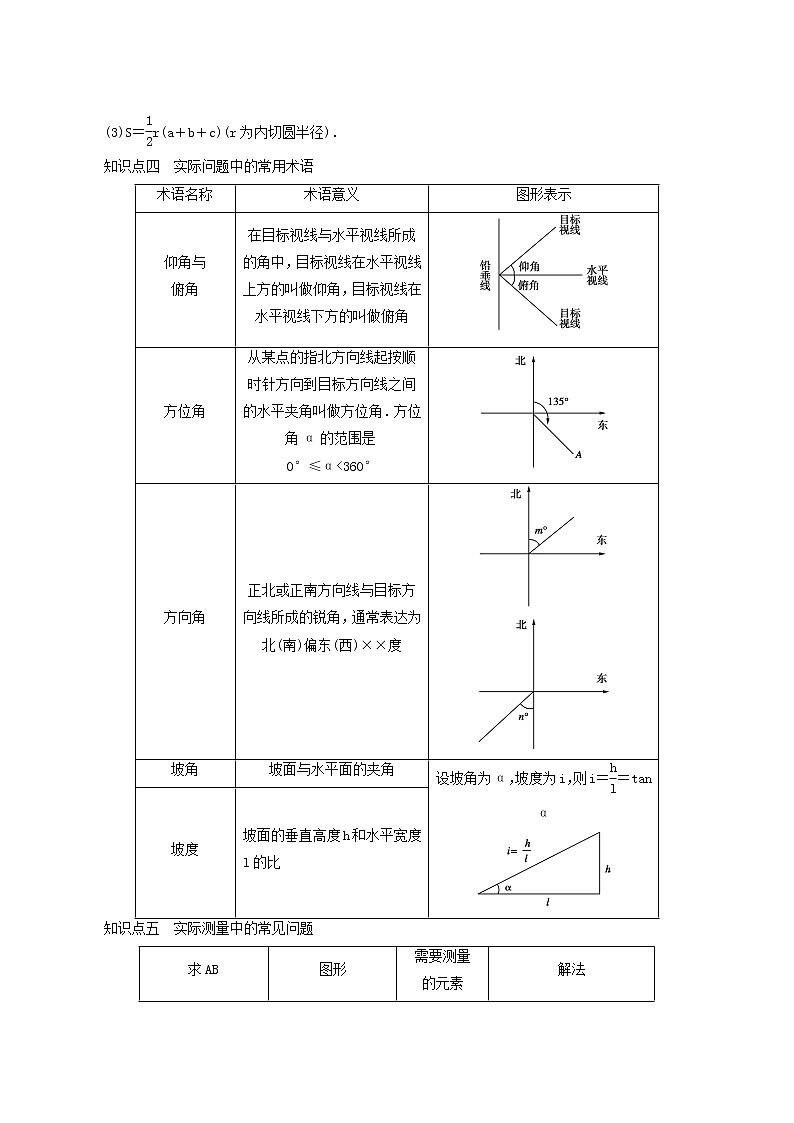
(1)S＝eq \f(1,2)a·ha(ha表示a边上的高)．
(2)S＝eq \f(1,2)absin C＝eq \f(1,2)acsin B＝eq \f(1,2)bcsin A.
(3)S＝eq \f(1,2)r(a＋b＋c)(r为内切圆半径)．
知识点四 实际问题中的常用术语
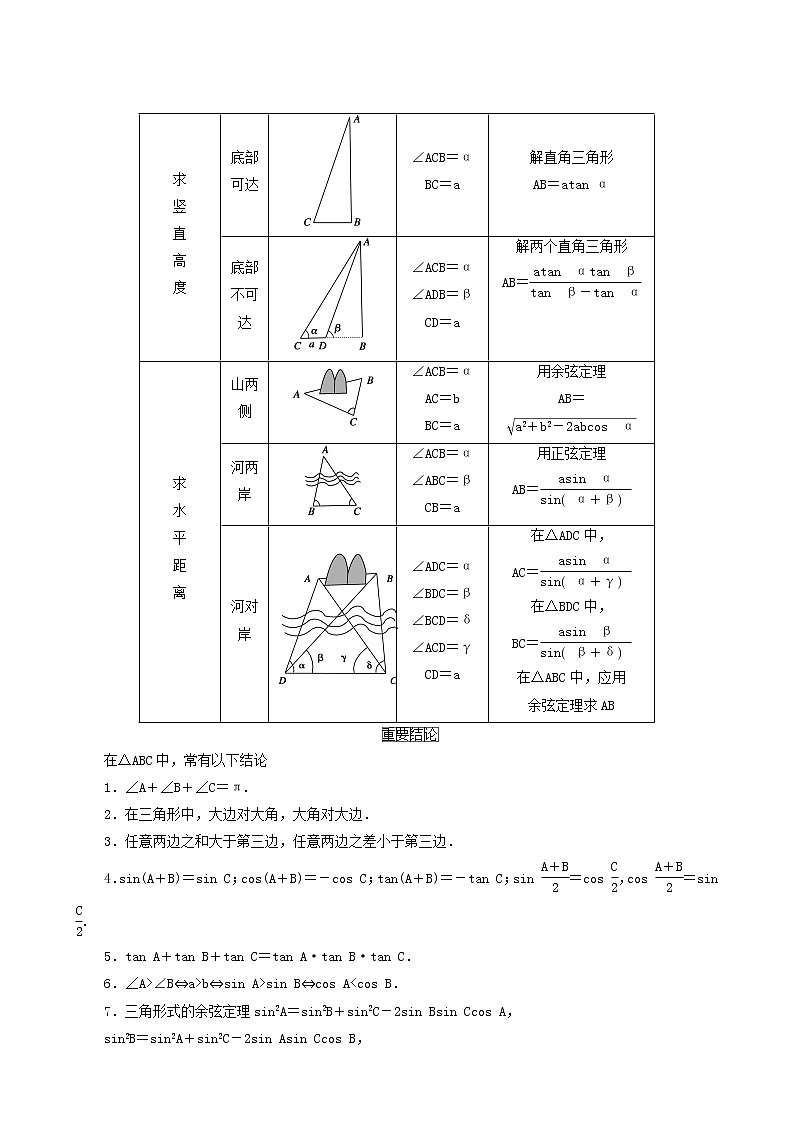
知识点五 实际测量中的常见问题
eq \x(重)eq \x(要)eq \x(结)eq \x(论)
在△ABC中，常有以下结论
1．∠A＋∠B＋∠C＝π.
2．在三角形中，大边对大角，大角对大边．
3．任意两边之和大于第三边，任意两边之差小于第三边．
4．sin(A＋B)＝sin C；cs(A＋B)＝－cs C；tan(A＋B)＝－tan C；sin eq \f(A＋B,2)＝cs eq \f(C,2)，cs eq \f(A＋B,2)＝sin eq \f(C,2).
5．tan A＋tan B＋tan C＝tan A·tan B·tan C．
6．∠A>∠B⇔a>b⇔sin A>sin B⇔cs AB必有sin A>sin B．( √ )
(2)在△ABC中，若b2＋c2>a2，则△ABC为锐角三角形．( × )
(3)在△ABC中，角A、B、C所对的边分别为a，b，c且a＝1，c＝eq \r(3)，A＝eq \f(π,6)，则b＝1或2.( √ )
(4)若满足条件C＝60°，AB＝eq \r(3)，BC＝a的△ABC有两个，则实数a的取值范围是(eq \r(3)，2)．( √ )
(5)在△ABC中，若bcs B＝acs A，则△ABC是等腰三角形．( × )
(6)俯角是铅垂线与视线所成的角，其范围为eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(π,2))).( × )
(7)方位角大小的范围是[0,2π)，方向角大小的范围一般是eq \b\lc\[\rc\)(\a\vs4\al\c1(0，\f(π,2))).( √ )
题组二 走进教材
2．(必修5P10A组T8改编)△ABC的内角A，B，C的对边分别为a，b，c.已知a＝eq \r(5)，c＝2，cs A＝eq \f(2,3)，则b＝( D )
A.eq \r(2) B．eq \r(3)
C．2 D．3
[解析] 由余弦定理，得4＋b2－2×2bcs A＝5，整理得3b2－8b－3＝0，解得b＝3或b＝－eq \f(1,3)(舍去)，故选D.
3．(必修5P10A组T3改编)△ABC的内角A，B，C的对边分别为a，b，c.已知C＝60°，b＝eq \r(6)，c＝3，则A＝( B )
A．45° B．75°
C．105° D．60°
[解析] 由题意：eq \f(b,sin B)＝eq \f(c,sin C)，即sin B＝eq \f(bsin C,c)＝eq \f(\r(6)×\f(\r(3),2),3)＝eq \f(\r(2),2)，结合b