高中数学5.4 三角函数的图象与性质教案配套ppt课件

这是一份高中数学5.4 三角函数的图象与性质教案配套ppt课件，共44页。

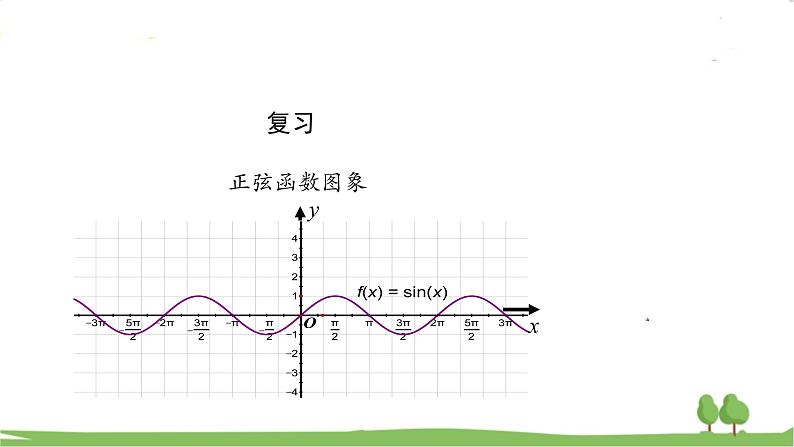
复习 正弦函数图象 y x
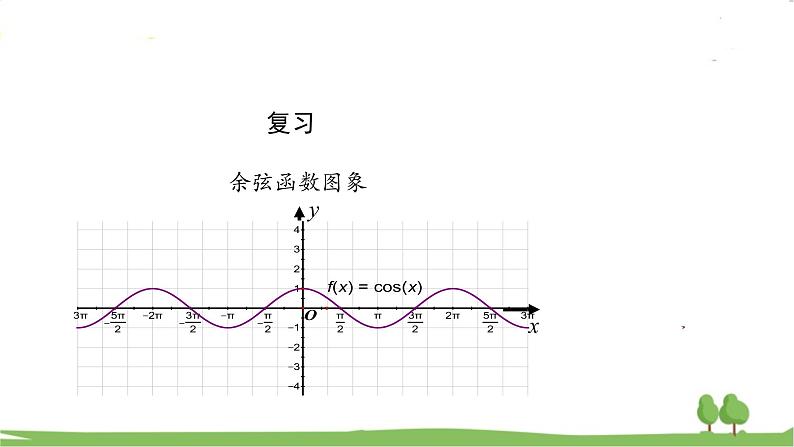
复习 余弦函数图象 y x
复习 三角函数图象、性质的应用
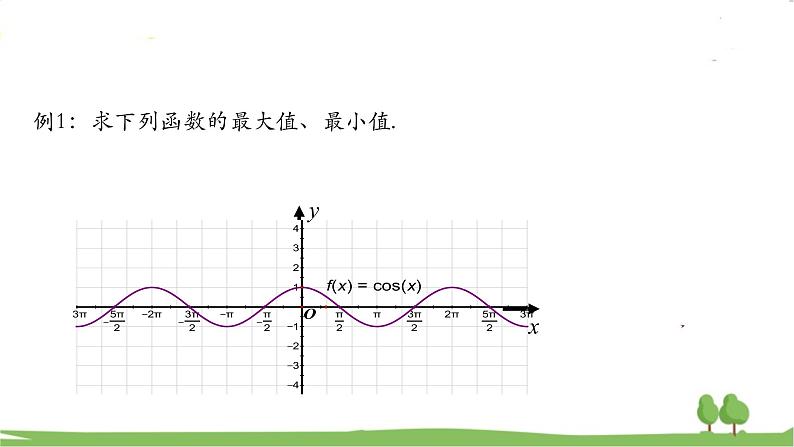
例1：求下列函数的最大值、最小值.

y x
例1：求下列函数的最大值、最小值.
例1：求下列函数的最大值、最小值. 分析：当 时， . 所以先解决 在 上的最大值、最小值.
y x
例1：求下列函数的最大值、最小值. 所以，当 时，函数取到最小值为0. 当 时，函数取到最大值为
例2：已知函数f(x)=csx，其中 ，若f(x)的值域是 ，求m的取值范围．
例2：已知函数f(x)=csx，其中 ，若f(x)的值域是 ，求m的取值范围． y x
例2：已知函数f(x)=csx，其中 ，若f(x)的值域是 ，求m的取值范围． y m x
例2：已知函数f(x)=csx，其中 ，若f(x)的值域是 ，求m的取值范围． 分析：通过观察余弦函数的图象，可以发现当 时， f(x)的值域是 .
思考1：已知函数 ，其中若f(x)的值域是 ，求m的取值范围．
思考1：已知函数 ，其中若f(x)的值域是 ，求m的取值范围．
分析：当 时， ，接下来只需处理f(x)=csx 在 上的值域是 . 这就转化为例2的情况.
在例2中， ，所以此题的m满足： 解得： .
思考2：已知函数 ，其中 ，若f(x)的值域是 ，求m的取值范围．
思考2：已知函数 ，其中 ，若f(x)的值域是 ，求m的取值范围．
分析：当 时， ，接下来只需考察f(x)=csx 在 的值域是 . 这就转化为了例2的情况.
在例2中， ，所以此题的m满足： 解得： .
例3：求不等式 的解集.
例3：求不等式 的解集.

y x
分析：通过观察正、余弦函数的图象，先计算出sinx=csx的解，进而得到不等式在 内的解. y x
思考：求不等式 的解集.
思考：求不等式 的解集.分析：不等式 可转化为：
y x
y x
思考：求不等式 的解集.
分析：在 内， 的解为 y x
分析：在R上， 的解集为. y x
小结 利用三角函数图象及性质研究函数的值域；
小结 利用三角函数图象及性质研究函数的值域；利用三角函数图象及性质研究一些不等式的解集.