高中数学人教A版 (2019)选择性必修 第一册1.3 空间向量及其运算的坐标表示习题ppt课件

这是一份高中数学人教A版 (2019)选择性必修 第一册1.3 空间向量及其运算的坐标表示习题ppt课件，文件包含132pptx、132DOC等2份课件配套教学资源，其中PPT共51页， 欢迎下载使用。

| 自 学 导 引 |
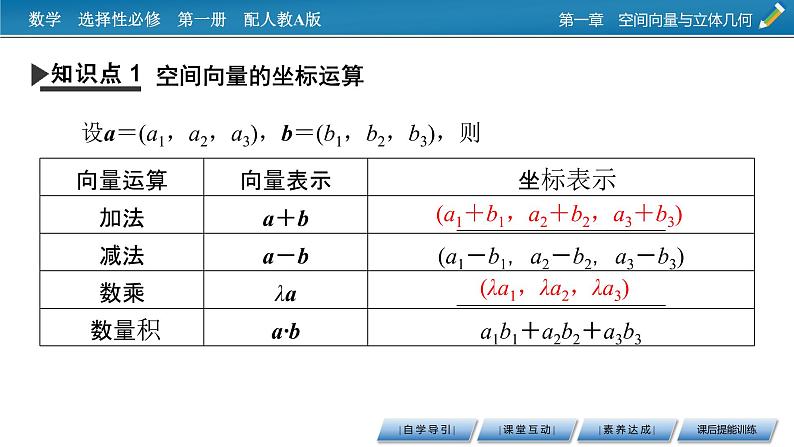
设a＝(a1，a2，a3)，b＝(b1，b2，b3)，则
(a1＋b1，a2＋b2，a3＋b3)　
(λa1，λa2，λa3)　
已知向量a＝(1,2,3)，b＝(－1,0,1)，则a＋2b＝(　　)A．(－1,2,5)　　B．(－1,4,5)C．(1,2,5)　　D．(1,4,5)【答案】A【解析】a＋2b＝(1,2,3)＋2(－1,0,1)＝(1,2,3)＋(－2，0,2)＝(－1,2,5)．故选A．
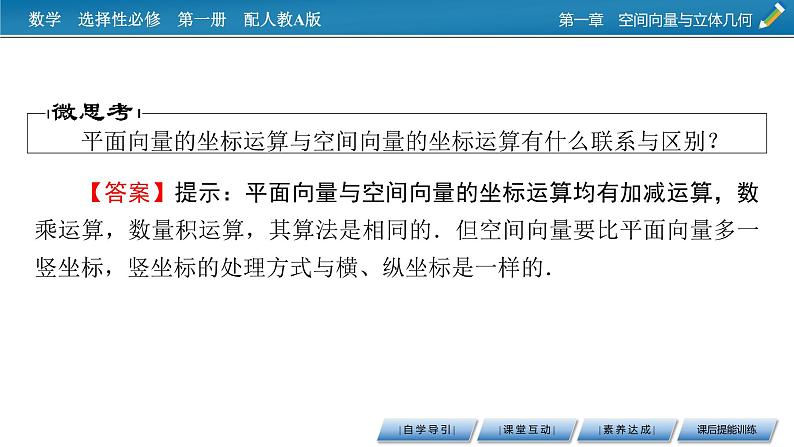
平面向量的坐标运算与空间向量的坐标运算有什么联系与区别？
【答案】提示：平面向量与空间向量的坐标运算均有加减运算，数乘运算，数量积运算，其算法是相同的．但空间向量要比平面向量多一竖坐标，竖坐标的处理方式与横、纵坐标是一样的．
1．空间向量平行和垂直的条件：(1)平行：a∥b(b≠0)⇔a＝λb⇔_______________________；(2)垂直：a⊥b⇔a·b＝0⇔__________________.2．空间向量的模及夹角的坐标计算公式：(1)模：|a|＝__________，|b|＝____________；(2)cs〈a，b〉＝_______________________.
a1＝λb1，a2＝λb2，a3＝λb　
空间向量的平行、垂直及模、夹角
a1b1＋a2b2＋a3b3＝0　
已知a＝(a1，a2，a3)，b＝(b1，b2，b3)，a∥b，且b1b2b3≠0，类比平面向量平行的坐标表示，可得到什么结论？
向量的坐标及两点间的距离公式
【预习自测】1．思维辨析(正确的画“√”，错误的画“×”)(1)空间两点间的距离公式是平面上两点间的距离公式的推广．(　　)(2)平面上两点间的距离公式是空间两点间距离公式的特例．(　　)(3)将距离公式中两点的坐标顺序互换，结果不变．(　　)【答案】(1)√　(2)√　(3)√
【解析】(1)空间中点的坐标比平面内点的坐标，多了竖坐标，此说法正确．(2)平面中点的坐标比空间内点的坐标，少了竖坐标，此说法正确．(3)由距离公式的特征可知，两点的坐标顺序互换，结果不变．
| 课 堂 互 动 |
　已知a＝(2，－1，－2)，b＝(0，－1,4)，求a＋b，2a·(－b)，(a＋b)·(a－b)．素养点睛：考查逻辑推理、数学运算的核心素养．【答案】解：a＋b＝(2，－1，－2)＋(0，－1,4)＝(2，－2,2)，2a·(－b)＝2(2，－1，－2)·(0,1，－4)＝14，又a－b＝(2，－1，－2)－(0，－1,4)＝(2,0，－6)，∴(a＋b)·(a－b)＝(2，－2,2)·(2,0，－6)＝－8.
题型1　空间向量的坐标运算
关于空间向量坐标运算的两类问题(1)直接计算问题首先将空间向量用坐标表示出来，然后准确运用空间向量坐标运算公式计算．(2)由条件求向量或点的坐标首先把向量用坐标形式设出来，然后通过建立方程组，解方程求出其坐标．
题型2　利用向量的坐标运算解决空间中的平行、垂直问题
2．(1)已知向量a＝(2,4,5)，b＝(3，x，y)分别是直线l1，l2的方向向量，若l1∥l2，求x，y；(2)已知向量a＝(1,1,0)，b＝(－1,0,2)，且ka＋b与2a－b互相垂直，求k的值．
方向2　向量法求距离 　如图，以棱长为1的正方体的三条棱所在直线为坐标轴，建立空间直角坐标系Oxyz，点P在线段AB上，点Q在线段DC上．(1)当PB＝2AP，且点P关于y轴的对称点为点M时，求|PM|的长度；(2)当点P是面对角线AB的中点，点Q在面对角线DC上运动时，探究|PQ|的最小值．
素养点睛：考查逻辑推理、数学运算的核心素养．
1．向量夹角的计算步骤(1)建系：结合图形建立适当的空间直角坐标系，建系原则是让尽可能多的点落到坐标轴上．(2)求方向向量：依据点的坐标求出方向向量的坐标．(3)代入公式：利用两向量的夹角公式将方向向量的坐标代入求出夹角．2．求空间两点间的距离的关键及步骤(1)求空间两点间的距离问题就是把点的坐标代入距离公式进行计算，其中确定点的坐标或合理设出点的坐标是关键．
(2)若所给题目中未建立坐标系，需结合已知条件建立适当的坐标系，再利用空间两点间的距离公式计算．一般按如下的步骤：
3．已知向量a＝(x,1,2)，b＝(1，y，－2)，c＝(3,1，z)，且a∥b，b⊥c.(1)求向量a，b，c；(2)求向量a＋c与b＋c所成角的余弦值．
易错警示　由向量的夹角求参数的取值范围
错解分析：错误的根本原因是忽视了a·b<0包含〈a，b〉＝180°的情况．实际上a与b夹角为钝角⇔a·b<0且〈a，b〉≠180°.正解：选B．因为a与b的夹角为钝角，所以a·b<0且〈a，b〉≠180°.由a·b<0得(3，－2，－3)·(－1，x－1,1)＝3×(－1)＋(－2)·(x－1)＋(－3)×1<0，解得x>－2.若a与b的夹角为180°，则存在λ<0，使b＝λa，即(－1，x－1,1)＝λ(3，－2，－3)，
防范措施：1．明确两个充要条件(1)向量a与b的夹角为锐角⇔a·b>0且〈a，b〉≠0°.(2)向量a与b的夹角为钝角⇔a·b<0且〈a，b〉≠180°.2．注意向量共线情况的计算先利用a∥b⇔a＝λb⇔a1＝λb1，a2＝λb2，a3＝λb3，求出参数，再根据“λ>0，a与b同向，λ<0，a与b反向”确定满足题意的参数的值.
| 素 养 达 成 |
1．对空间向量坐标运算的两点说明(1)类比平面向量坐标运算：空间向量的加法、减法、数乘和数量积与平面向量类似，学习中可以类比推广．推广时注意利用向量的坐标表示，即向量在平面上是用唯一确定的有序实数对表示，即a＝(x，y)．而在空间中则表示为a＝(x，y，z)．(2)运算结果：空间向量的加法、减法、数乘坐标运算结果依然是一个向量；空间向量的数量积坐标运算的结果是一个实数．
2．对空间两个向量平行与垂直的两点说明(1)类比平面向量平行、垂直：空间两个向量平行、垂直与平面两个向量平行、垂直的表达式不一样，但实质是一致的．(2)转化：判定空间两直线平行或垂直只需判断两直线对应的方向向量是否平行或垂直．3．对空间两向量夹角与距离的四点说明(1)范围：空间两条直线夹角的范围与向量夹角的范围不同，当所求两向量夹角为钝角时，两直线夹角是与此钝角互补的锐角．
1．已知a＝(2，－3,1)，则下列向量中与a平行的是(　　)A．(1,1,1)B．(－2，－3,5)C．(2，－3,5)D．(－4,6，－2)【答案】D【解析】若b＝(－4,6，－2)，则b＝－2(2，－3,1)＝－2a，所以a∥b.
2．已知点A(1,5，－2)，B(2,4,1)，C(a,3，b＋2)共线，那么a－b等于(　　)A．5B．1C．－5D．－1【答案】B
4．已知向量a＝(2,4，x)，b＝(2，y,2)，若|a|＝6，且a⊥b，则x＋y的值为________．【答案】1或－3