2021-2022学年内蒙古呼伦贝尔市满洲里一中高二（下）期末数学试卷（理科）（Word解析版）

绝密★启用前

2021-2022学年内蒙古呼伦贝尔市满洲里一中高二（下）期末数学试卷（理科）

注意事项:
1.答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案写在答题卡上，写在试卷上无效。
3.考试结束后，本试卷和答题卡一并交回。

第I卷（选择题）

一、单选题（本大题共12小题，共60.0分。在每小题列出的选项中，选出符合题目的一项）

1. 集合，，则(    )

A.  B.  C.  D.

2. 用系统抽样的方法从名学生中抽取容量为的样本，将名学生编号为至，按编号顺序分组，若在第组抽出的号码为，则在第一组抽出的号码为(    )

A.  B.  C.  D.

3. “”是“”成立的(    )

A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件

4. 下列函数中，既是奇函数，又在定义域上单调递增的是(    )

A.  B.  C.  D.

5. 若函数是奇函数，当时，，则(    )

A.  B.  C.  D.

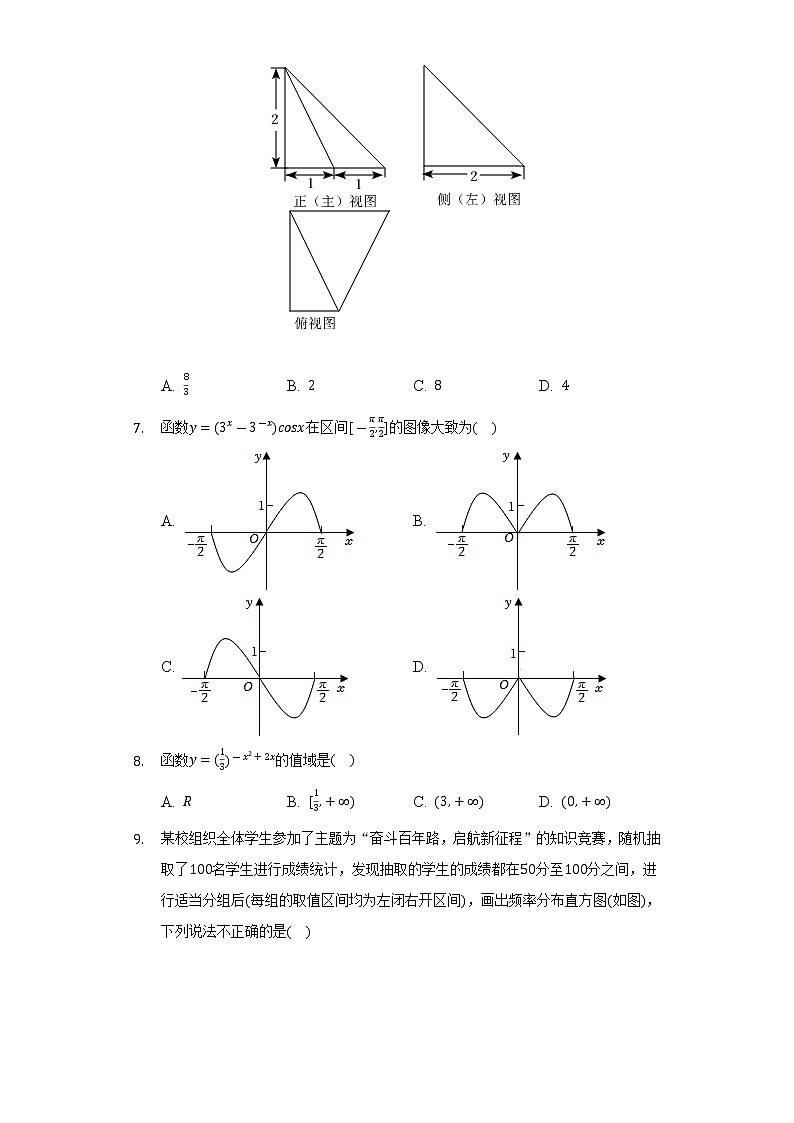
6. 某几何体的三视图如图所示，则该几何体的体积是(    )

A.  B.  C.  D.

7. 函数在区间的图像大致为(    )

A.  B.
C.  D.

8. 函数的值域是(    )

A.  B.  C.  D.

9. 某校组织全体学生参加了主题为“奋斗百年路，启航新征程”的知识竞赛，随机抽取了名学生进行成绩统计，发现抽取的学生的成绩都在分至分之间，进行适当分组后每组的取值区间均为左闭右开区间，画出频率分布直方图如图，下列说法不正确的是(    )

A. 在被抽取的学生中，成绩在区间内的学生有人
B. 这名学生成绩的众数为
C. 估计全校学生成绩的平均分数为
D. 这名学生成绩的中位数为

10. 若的展开式中的系数为，则(    )

A.  B.  C.  D.

11. 已知正三棱柱，底面正三角形的边长为，侧棱长为，则点到平面的距离为(    )

A.  B.  C.  D.

12. 已知函数，若有个零点，则实数的取值范围是(    )

A.  B.  C.  D.

第II卷（非选择题）

二、填空题（本大题共4小题，共16.0分）

13. 已知函数，则______．
14. 设函数在区间上为偶函数，则的值为______．
15. 已知函数在区间上单调递增，则实数的取值范围是______．
16. 在四面体中，平面，，，则该四面体外接球的表面积为______．

三、解答题（本大题共5小题，共56.0分。解答应写出文字说明，证明过程或演算步骤）

17. 为抗击新冠肺炎，某单位组织中、老年员工分别进行疫苗注射，共分为三针接种，只有三针均接种且每针接种后经检测合格，才能说明疫苗接种成功每针接种后是否合格相互之间没有影响根据大数据比对，中年员工甲在每针接种合格的概率分别为；老年员工乙在每针接种合格的概率分别为．
    甲、乙两位员工中，谁接种成功的概率更大？
    若甲和乙均参加疫苗接种，求两人中至少有一人接种成功的概率．
18. 如图所示，四棱锥中，平面平面，底面是边长为正方形，，与交于点，点在线段上．
    求证：平面；
    若平面，求平面与平面所成夹角的余弦值．

19. 已知函数．
    ，求函数在处的切线方程；
    讨论函数的单调性．
20. 在平面直角坐标系中，曲线的参数方程为为参数，以原点为极点，轴的非负半轴为极轴建立极坐标系，直线的极坐标方程为．
    求曲线的普通方程与直线的直角坐标方程；
    设直线与曲线交于，两点，点的坐标为，求的值．
21. 设，，均为正数，且．
    求的最小值；
    证明：．
    

答案和解析

1.【答案】 

【解析】解：，，
．
故选：．
根据已知条件，结合交集的定义，即可求解．
本题主要考查交集及其运算，属于基础题．
 

2.【答案】 

【解析】解：样本间距为，
若组抽出的号码为，则在第一组抽出的号码为，
故选：．
根据系统抽样的定义和性质即可得到结论．
本题主要考查系统抽样的应用，确定样本间距是解决本题的关键．比较基础．
 

3.【答案】 

【解析】解：若，则，则成立，即充分性成立，
若当时，成立，但不成立，即必要性不成立，
即“”是“”成立的充分不必要条件，
故选：．
根据不等式的关系结合充分条件和必要条件的定义进行判断即可．
本题主要考查充分条件和必要条件的判断，根据不等式的性质结合充分条件和必要条件的定义是解决本题的关键．
 

4.【答案】 

【解析】解：函数为偶函数，故A不符合题意；
，函数为奇函数，
当时，，时，，
函数在定义域上不是单调递增函数，故B不符合题意；
，函数为奇函数，
当时，，为减函数，故C不符合题意，
，函数是奇函数，
又函数在定义域上单调递增，函数在定义域上单调递减，
函数在定义域上单调递增，故D符合题意．
故选：．
利用函数的奇偶性与单调性逐项判断即可得出结论．
本题主要考查函数奇偶性与单调性的判断，掌握常见函数的性质是解题的关键，属于基础题．
 

5.【答案】 

【解析】解：根据题意，当时，，所以，
又由为奇函数，所以，
故选：．
根据题意，由函数的解析式求出的值，结合函数的奇偶性分析可得答案．
本题考查函数奇偶性的性质以及应用，涉及函数值的计算，属于基础题．
 

6.【答案】 

【解析】解：根据三视图还原，得到四棱锥，其底面为直角梯形，高为，
体积为，
故选：．
画出几何体的图形，利用三视图的数据求解几何体的体积即可．
本题考查三视图求解几何体的体积，判断几何体的形状是解题的关键，是中档题．
 

7.【答案】 

【解析】解：，
可知，
函数是奇函数，排除；
当时，，排除．
故选：．
判断函数的奇偶性，结合函数的特殊值判断点的位置，推出选项即可．
本题考查函数的奇偶性以及函数的图象的判断，是中档题．
 

8.【答案】 

【解析】解：令，则，
而，所以，
所以函数的值域为
故选：．
先求出函数的范围，再根据指数函数的性质即可求解．
本题考查了指数函数的值域，涉及到二次函数的值域的求解，考查了学生的运算能力，属于基础题．
 

9.【答案】 

【解析】解：对于，成绩在区间内的学生有人，A正确；
对于，名学生成绩的众数为最高小长方形中点横坐标，，B正确；
对于，，C错误；
对于，的频率为，
的频率为，
故中位数位于之间，设中位数为，

解得：，D正确．
故选：．
根据频率分布直方图计算即可．
本题考查由频率分布直方图求频数、频率、中位数、众数、平均数，属于基础题．
 

10.【答案】 

【解析】解：由于的展开式中的系数为，则，
故选：．
由题意利用二项展开式的通项公式，求得的值．
本题主要考查二项式定理的应用，二项展开式的通项公式，属于中档题．
 

11.【答案】 

【解析】解：如图，设与相交于点，则为的中点，
点到平面的距离等于点到平面的距离，
取中点，连接，，底面为正三角形，，
又底面，底面，，且，
平面，在平面内过作，垂足的为，
，又，
平面，
即为所求，
又在中，，易知，斜边，
根据面积的等面积算法可得，
故点到平面的距离为．
故选：．
根据化归转化思想，线面垂直判定定理，线面垂直性质定理即可求解．
本题考查化归转化思想，线面垂直判定定理，线面垂直性质定理，等面积算法，属基础题．
 

12.【答案】 

【解析】解：令，得，
在同一坐标系中作出，的图象，如图所示：

由图象知：若有个零点，
则实数的取值范围是．
故选：．
在同一坐标系中作出，的图象，根据有个零点求解．
本题考查了函数的零点、转化思想、数形结合思想，属于基础题．
 

13.【答案】 

【解析】解：，

，
故答案为：．
结合分段函数，根据自变量的值代入化简即可．
本题考查了分段函数的应用，属于基础题．
 

14.【答案】 

【解析】解：根据题意，因为函数在区间上为偶函数，
必有，即，解得．
又二次函数为偶函数，则其对称轴为轴，
必有，则有，
所以；
故答案为：．
根据题意，由偶函数的定义域要求可得的值，结合二次函数的性质可得的值，计算可得答案．
本题考查函数奇偶性的性质以及应用，涉及函数的定义域，属于基础题．
 

15.【答案】 

【解析】解：由题设，，
所以上恒成立，即恒成立，
而在上单调递增，所以，
故，即实数的取值范围是．
故答案为：．
求求导，由题意可得在上恒成立，利用参变量分离法即可求解的取值范围．
本题主要考查利用导数研究函数的单调性，考查转化思想与运算求解能力，属于基础题．
 

16.【答案】 

【解析】解：，，
，
平面，
为球的直径，
，
则球的表面积为，
故答案为：．
根据条件，确定为球的直径，求出球的半径，即可求出该四面体外接球的表面积．
本题主要考查空间几何体的位置关系，考查该四面体外接球的表面积，确定为球的直径是本题的突破点．
 

17.【答案】解：记中年员工甲接种成功的事件为，老年员工乙接种成功的事件为，
则，，
因为，
故中年员工甲接种成功的概率更大．
记甲和乙两人中至少有一人接种成功的事件记为，
则，
则． 

【解析】记中年员工甲接种成功的事件为，老年员工乙接种成功的事件为，利用独立事件的概率公式分别求出，，再比较两者大小即可．
利用间接法求解．
本题主要考查了独立事件的概率公式，属于基础题．
 

18.【答案】证明：因为平面平面且交线为，
又平面且，所以平面，
又平面，所以，
因为是边长为正方形，所以，又，
所以，即，
又因为，，平面，
所以平面；
解：因为平面，平面，平面平面，
所以，
因为为的中点，所以为的中点，
以，，分别为轴，轴，轴建立空间直角坐标系，
则有，，
易得平面的一个法向量为，
设平面的一个法向量为，
则，
取，则，
设平面与平面所成夹角为，则，
所以平面与平面所成夹角的余弦值为．
 

【解析】根据面面垂直的性质可得平面，进而得到，结合勾股定理证明即可证明平面；
以，，分别为轴，轴，轴建立空间直角坐标系，分别求平面与平面的一个法向量，进而求得二面角夹角的余弦值即可．
本题考查了线面垂直的证明和二面角的计算，属于中档题．
 

19.【答案】解：当时，，
切线的斜率，，则切线方程为，即．
函数的定义域为，且，
当时，，由，得；由，得．
则函数的单调递增区间为，单调递减区间为．
当，即时，由，得或；由，得．
则函数的单调递增区间为，，
函数的单调递减区间为．
当，即时，恒成立，则函数的单调递增区间为．
当，即时，由，得或；由，得，
则函数的单调递增区间为，，函数的单调递减区间为．
综上所述，当时，函数在上单调递增，在上单调递减；
当时，函数在和上单调递增，在上单调递减；
当时，函数在上单调递增；
当时，函数在和上单调递增，在上单调递减． 

【解析】当时，求出的解析式，对求导，利用导数的几何意义求出切线斜率，求出，利用点斜式即可求得切线方程；
对求导，再对分类讨论，利用导数与单调性的关系求解即可．
本题主要考查利用导数研究函数的单调性，利用导数研究曲线上某点的切线方程，考查分类讨论思想与运算求解能力，属于中档题．
 

20.【答案】解：由曲线，转换为普通方程为．
直线，则，
根据，转换为直角坐标方程为．
直线的标准参数方程为：其中为参数，
设，两点分别对应的参数为，，
将直线的参数方程代入椭圆的方程可得：，
即
所以，．
所以
所以的值为． 

【解析】直接利用转换关系，在参数方程、极坐标方程和直角坐标方程之间进行转换；
利用一元二次方程根和系数关系式的应用求出结果．
本题考查的知识要点：参数方程、极坐标方程和直角坐标方程之间的转换，一元二次方程根和系数关系式的应用，主要考查学生的运算能力和数学思维能力，属于中档题．
 

21.【答案】解：，均为正数，且，
，
当且仅当，即， 时，等号成立，
故的最小值为．
法一：证明：由柯西不等式可得，，即，
当且仅当，等号成立．
法二：证明：分析法要证明，
只需证明  ，
只需证明  ，
只需证明，
因为，当且仅当，即时，等号成立．
综上所述：． 

【解析】由已知结合乘法及基本不等式即可求解；
法一：证明：由柯西不等式即可直接证明，
法二：结合分析法，要证明，只需证明  ，只需证明  ，只需证明   ，然后结合基本不等式即可求证．
本题主要考查了基本不等式，柯西不等式在不等式证明中的应用，还考查了最值求解，属于中档题．