人教版 八年级上册 数学 课件 第十二章 全等三角形（复习）(共14张PPT)

这是一份人教版 八年级上册 数学 课件 第十二章 全等三角形（复习）(共14张PPT)，共14页。PPT课件主要包含了牛刀小试，知识总结，定义重合法，SSS，SAS，ASA，AAS，包括直角三角形，我能行，能力提高等内容，欢迎下载使用。
教学目标：1、通过基本训练，巩固第十二章所学的基本内容.2、通过练习题的学习和综合运用，加深理解第十二章所学的基本内容，发展能力.
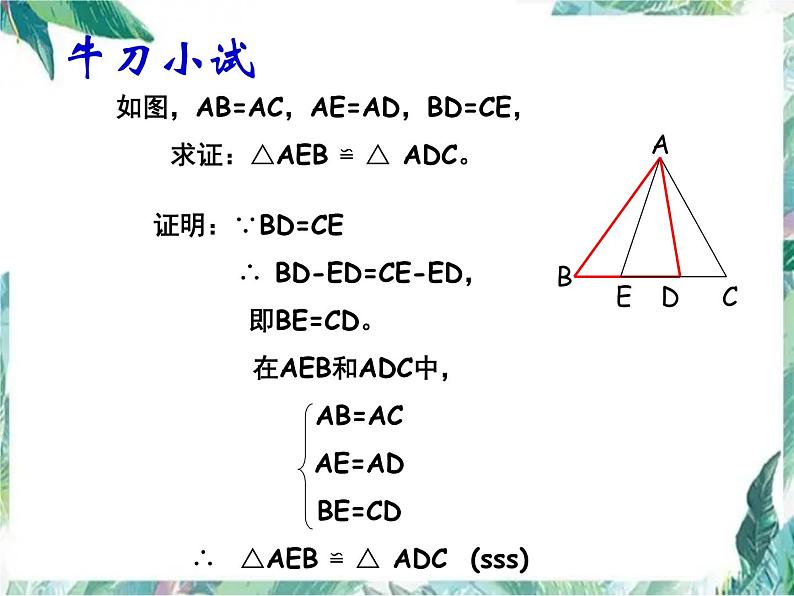
如图，AB=AC，AE=AD，BD=CE，求证：△AEB ≌ △ ADC。
证明：∵BD=CE ∴ BD-ED=CE-ED， 即BE=CD。
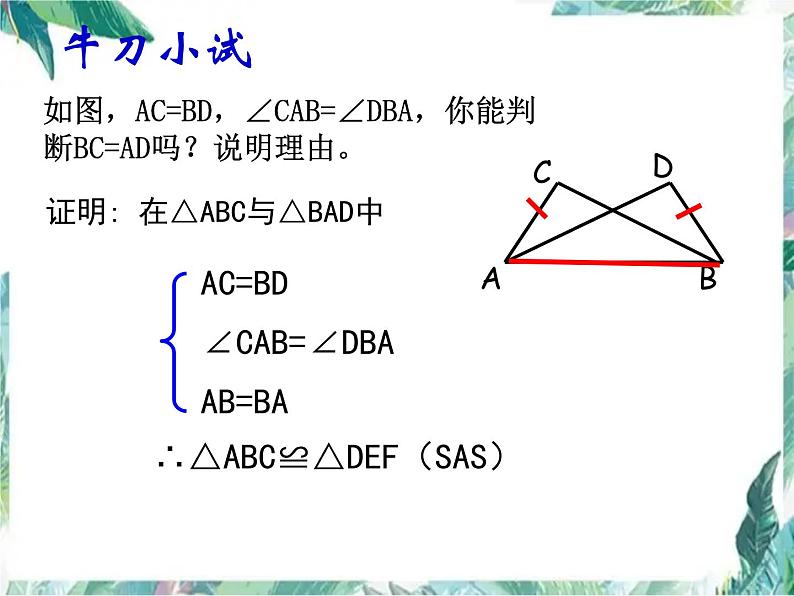
如图，AC=BD，∠CAB=∠DBA，你能判断BC=AD吗？说明理由。
证明: 在△ABC与△BAD中
AC=BD∠CAB=∠DBAAB=BA
∴△ABC≌△DEF（SAS）
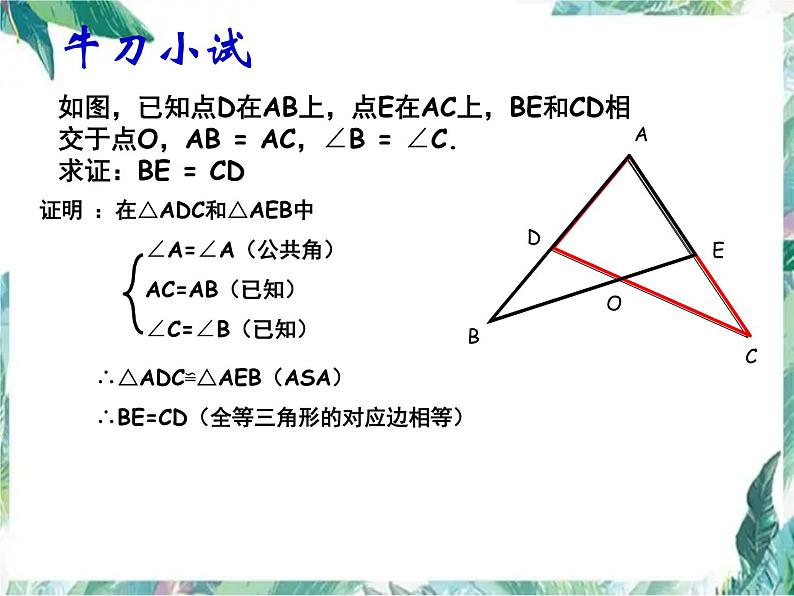
如图，已知点D在AB上，点E在AC上，BE和CD相交于点O，AB = AC，∠B = ∠C.求证：BE = CD
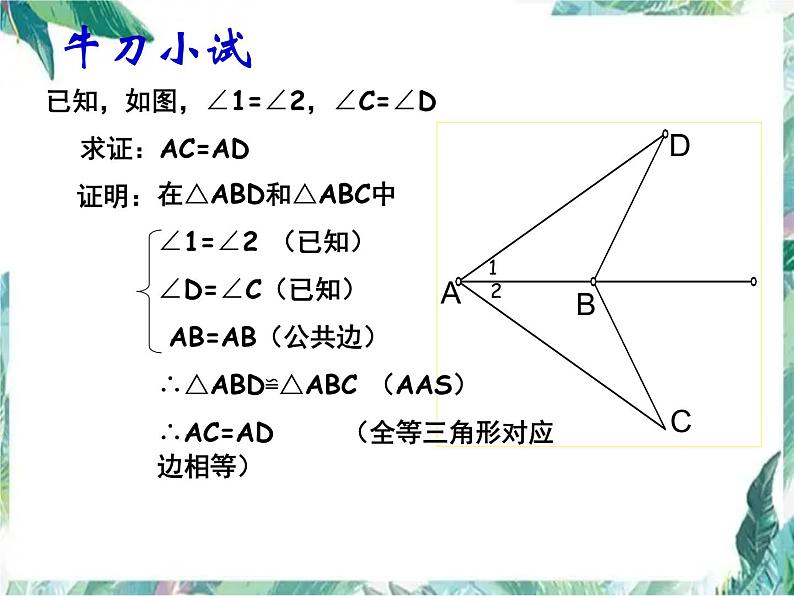
已知，如图，∠1=∠2，∠C=∠D 求证：AC=AD
在△ABD和△ABC中∠1=∠2 （已知）∠D=∠C（已知） AB=AB（公共边）∴△ABD≌△ABC （AAS）∴AC=AD （全等三角形对应边相等）
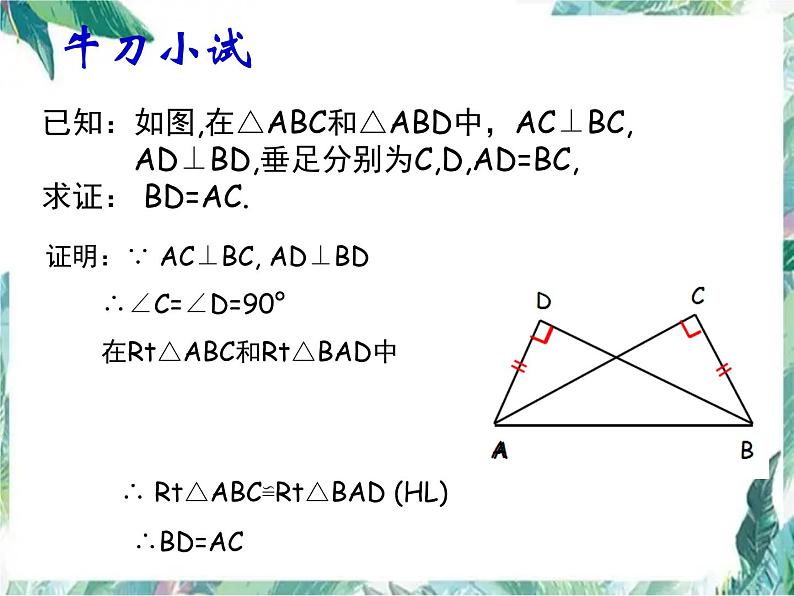
已知：如图,在△ABC和△ABD中，AC⊥BC, AD⊥BD,垂足分别为C,D,AD=BC,求证： BD=AC.
证明：∵ AC⊥BC, AD⊥BD ∴∠C=∠D=90° 在Rt△ABC和Rt△BAD中
∴ Rt△ABC≌Rt△BAD (HL)
一般三角形 全等的条件：
直角三角形 全等特有的条件：
不包括其它形状的三角形
“三月三，放风筝”下图是小东同学自己做的风筝，他根据AB=AD,BC=DC，不用度量，就知道∠ABC=∠ADC。请用所学的知识给予说明。
∴△ADC≌△ABC(SSS)
∴ ∠ABC=∠ADC(全等三角形的对应角相等)
在△ABC和△ADC中，
如图，CD＝CA，∠1＝∠2，EC＝BC.求证：DE＝AB.
如图，∠ACB=90°,AC=BC，BE⊥CE，AD⊥CE. 求证：△ACD≌△CBE.
证明两个三角形全等的基本思路：
找这边的另一个邻角(ASA)
找这个角的另一个边(SAS)
找这边的对角 (AAS)
已知角是直角，找一边(HL)
找两角的夹边(ASA)
找夹边外的任意边(AAS)
本节课你还有不理解的地方吗？