人教版八年级上册 复习专题：构造全等三角形(常见辅助线法)(共27张PPT)

这是一份人教版八年级上册 复习专题：构造全等三角形(常见辅助线法)(共27张PPT)，共27页。PPT课件主要包含了连线构造全等，第二关，倍长中线，第三关，截长补短，第四关，第五关等内容，欢迎下载使用。
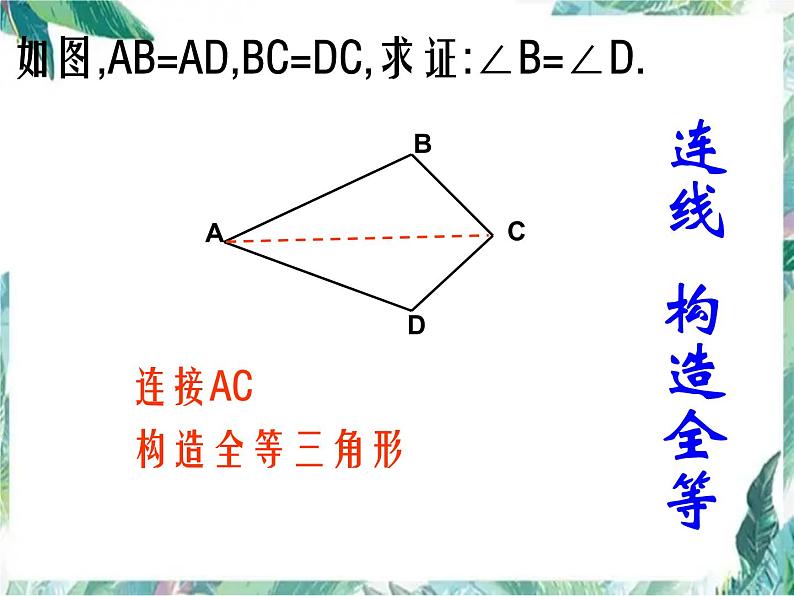
如图,AB=AD,BC=DC,求证:∠B=∠D.
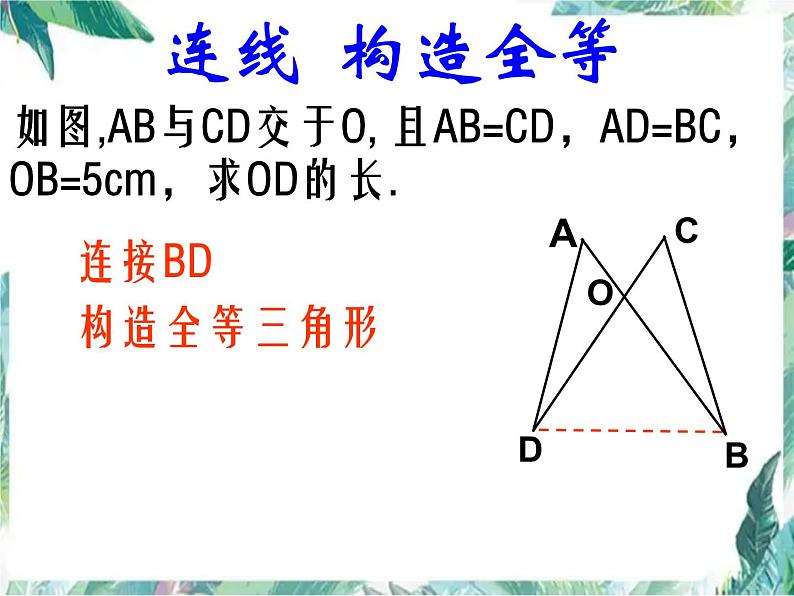
如图,AB与CD交于O, 且AB=CD，AD=BC，OB=5cm，求OD的长.
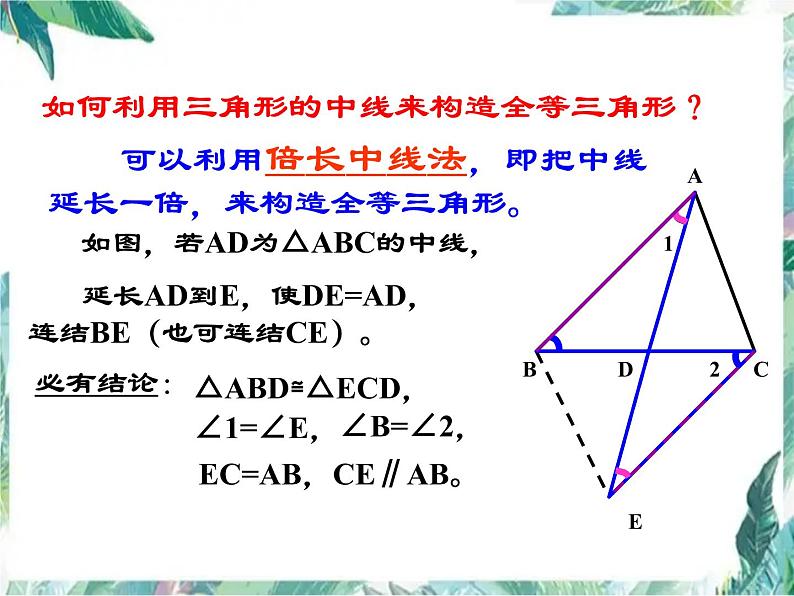
如何利用三角形的中线来构造全等三角形？
可以利用倍长中线法，即把中线延长一倍，来构造全等三角形。
如图，若AD为△ABC的中线，
延长AD到E，使DE=AD，连结BE（也可连结CE）。
EC=AB，CE∥AB。
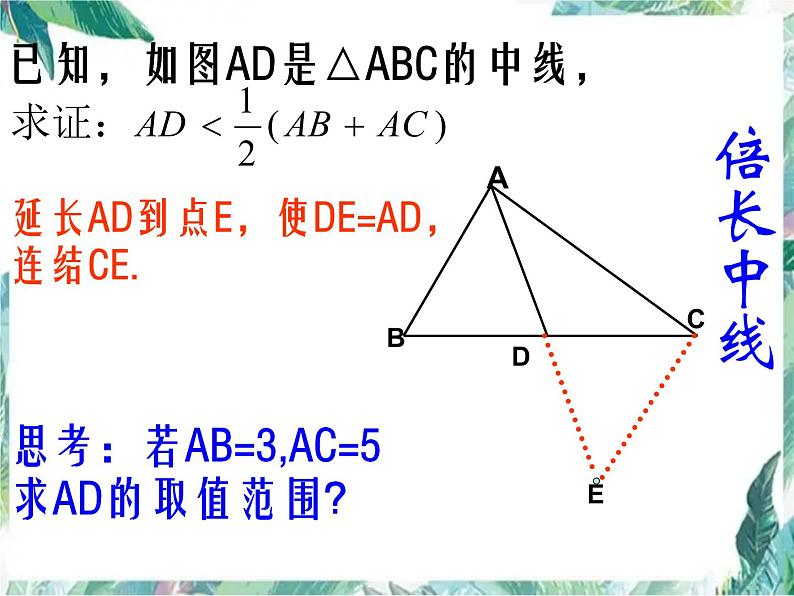
已知，如图AD是△ABC的中线，
延长AD到点E，使DE=AD，连结CE.
思考：若AB=3,AC=5求AD的取值范围？
已知在△ABC中，∠C=2∠B, ∠1=∠2求证:AB=AC+CD
在AB上取点E使得AE=AC，连接DE
在AC的延长线上取点F使得CF=CD，连接DF
如图所示，已知AD∥BC，∠1=∠2，∠3=∠4，直线DC经过点E交AD于点D，交BC于点C。求证：AD+BC=AB
在AB上取点F使得AF=AD,连接EF
已知：如图，在四边形ABCD中，BD是∠ABC的角平分线，AD=CD，求证：∠A+∠C=180°
在BC上截取BE，使BE=AB，连结DE。
∵ BD是∠ABC的角平分线（已知）∴∠1=∠2（角平分线定义）在△ABD和△EBD中∵ AB=EB（已知） ∠1=∠2（已证） BD=BD（公共边）∴△ABD≌△EBD（S.A.S）
∵ ∠3+ ∠4＝180°（平角定义），∠A＝∠3（已证）∴∠A+ ∠C＝180° （等量代换）
∴ ∠A＝∠3（全等三角形的对应角相等）
∵ AD=CD（已知），AD=DE（已证）∴DE=DC（等量代换）
∴∠4=∠C（等边对等角）
AD=DE（全等三角形的对应边相等）
延长BA到F，使BF=BC，连结DF。
∵ BD是∠ABC的角平分线（已知）∴∠1=∠2（角平分线定义）在△BFD和△BCD中∵ BF=BC（已知） ∠1=∠2（已证） BD=BD（公共边）∴△BFD≌△BCD（S.A.S）
∵ ∠F＝∠C（已证）∴∠4=∠C（等量代换）
∴ ∠F＝∠C（全等三角形的对应角相等）
∵ AD=CD（已知），DF=DC（已证）∴DF=AD（等量代换）
∴∠4=∠F（等边对等角）
∵ ∠3+ ∠4＝180° （平角定义）∴∠A+ ∠C＝180° （等量代换）
DF=DC（全等三角形的对应边相等）
如图，已知△ABC中，AD是∠BAC的角平分线，AB=AC+CD，求证：∠C=2∠B
在AB上截取AE，使AE=AC，连结DE。
∵ AD是∠BAC的角平分线（已知）∴∠1=∠2（角平分线定义）在△AED和△ACD中∵ AE=AC（已知） ∠1=∠2（已证） AD=AD（公共边）∴△AED≌△ACD（S.A.S）
∴∠B=∠4（等边对等角）
∴ ∠C＝∠3（全等三角形的对应角相等)
又∵ AB=AC+CD=AE+EB（已知）∴EB=DC=ED（等量代换）
∵ ∠3= ∠ B+∠4= 2∠B（三角形的一个外角等于和它不相邻的两个内角和）∴∠C=2∠B（等量代换）
ED=CD（全等三角形的对应边相等）
延长AC到F，使CF=CD，连结DF。
∵ AD是∠BAC的角平分线（已知）∴∠1=∠2（角平分线定义）∵ AB=AC+CD，CF=CD（已知）∴ AB=AC+CF=AF（等量代换）
∵ ∠ACB= 2∠F（三角形的一个外角等于和它不相邻的两个内角和）∴∠ACB=2∠B（等量代换）
在△ABD和△AFD中∵ AB=AF（已证） ∠1=∠2（已证） AD=AD（公共边）∴△ABD≌△AFD（S.A.S）
∴ ∠F＝∠B（全等三角形的对应角相等）
∵ CF=CD（已知）∴∠B=∠3（等边对等角）
如图，已知直线MN∥PQ，且AE平分∠BAN、BE平分∠QBA，DC是过E的任意线段，交MN于点D，交PQ于点C。求证：AD+AB=BC。
延长AE，交直线PQ于点F。
1.如图,△ABC中,∠C=90,AC=BC,AD平分∠ACB, DE⊥AB.若AB=6cm,则△DBE的周长是多少?
Ⅴ.“周长问题”的转化 借助“角平分线性质”
2.如图,△ABC中, D在AB的垂直平分线上,E在AC的垂直平分线上.若BC=6cm,求△ADE的周长.
Ⅴ.“周长问题”的转化 借助“垂直平分线性质”
5.如图, △ABC中，BP、CP是△ABC的角平分线，MN//BC.若BC=6cm, △AMN周长为13cm，求△ABC的周长.
Ⅴ.“周长问题”的转化 借助“等腰三角形性质”
AM+ BM+AN+NC+6
AM+ MP+AN+NP+6
△ABC中,AB＞AC ，∠A的平分线与BC的垂直平分线DM相交于D，过D作DE ⊥AB于E，作DF⊥AC于F。 求证：BE=CF
垂直平分线上点向两端连线段
如图，已知三角形ABC中,BC边上的垂直平分线DE与角BAC的平分线交于点E，EF垂直AB交AB的延长线于点F，EG垂直AC交AC于点G。求证：(1)BF=CG (2)判定AB+AC与AF的关系
如图,△ABC中, ∠C =90,BC=10,BD=6, AD平分∠BAC,求点D到AB的距离.
过点D作DE⊥AB于点E
角平分线上的点向角两边做垂线段
作DM⊥BC于M，DN⊥BA交BA的延长线于N。
∵ BD是∠ABC的角平分线（已知）∴∠1=∠2（角平分线定义）∵ DN⊥BA，DM⊥BC（已知）∴∠N=∠DMB=90°（垂直的定义）在△NBD和△MBD中∵ ∠N=∠DMB （已证） ∠1=∠2（已证） BD=BD（公共边）∴△NBD≌△MBD（A.A.S）
∴ ∠4=∠C（全等三角形的对应角相等）
∴ ND=MD（全等三角形的对应边相等）
∵ DN⊥BA，DM⊥BC（已知）∴△NAD和△MCD是Rt△在Rt△NAD和Rt△MCD中∵ ND=MD （已证） AD=CD（已知）∴Rt△NAD≌Rt△MCD（H.L）
∵ ∠3+ ∠4＝180°（平角定义）， ∠A＝∠3（已证）∴∠A+ ∠C＝180°（等量代换）
如图,OC 平分∠AOB,
角平分线上点向两边作垂线段
过点P作PF⊥OA,PG ⊥OB垂足为点F,点G
∠DOE +∠DPE =180°