2021-2022学年河北省保定市涿州市八年级（下）期末数学试卷（Word解析版）

绝密★启用前

2021-2022学年河北省保定市涿州市八年级（下）期末数学试卷

注意事项:
1.答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案写在答题卡上，写在试卷上无效。
3.考试结束后，本试卷和答题卡一并交回。

第I卷（选择题）

一、选择题（本大题共15小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）

1. 下面是二次根式的是(    )

A.  B.  C.  D.

2. 如图，四边形是平行四边形，点在线段的延长线上，若，则(    )

A.  B.  C.  D. 都不对

3. 如图，已知矩形中，下列条件能使矩形成为正方形的是(    )

A.
B.
C.
D.

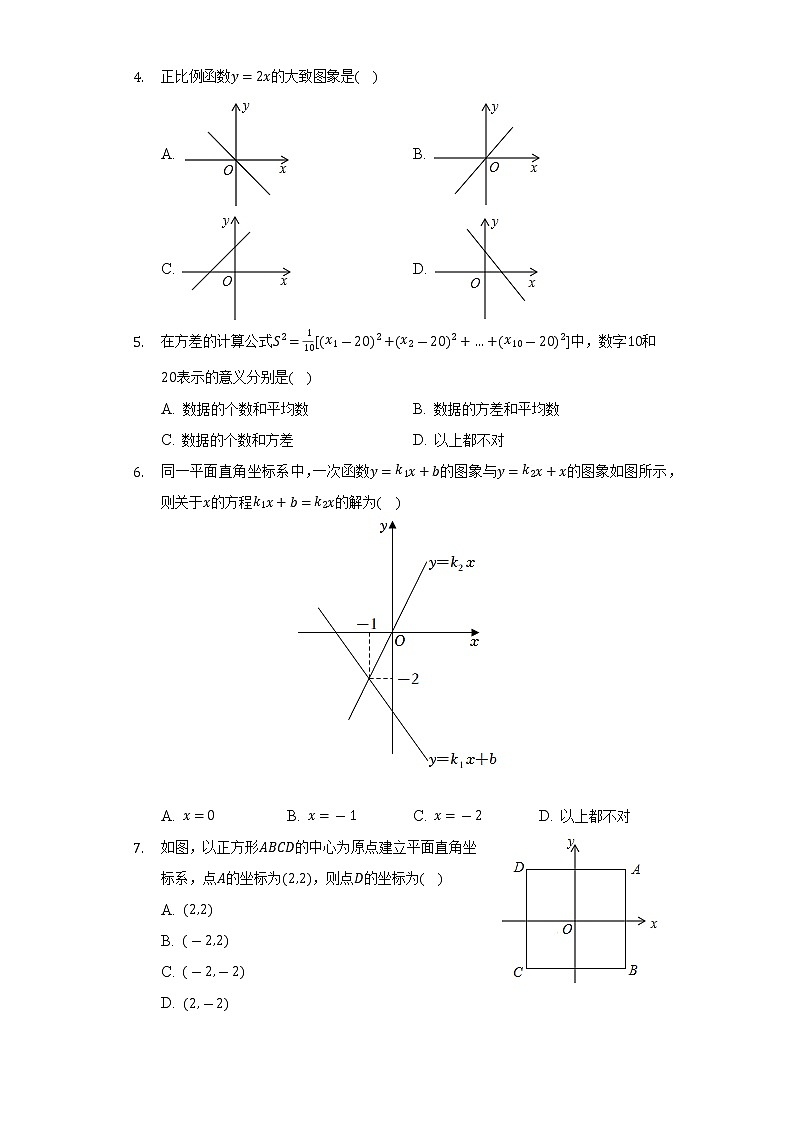
4. 正比例函数的大致图象是(    )

A.  B.
C.  D.

5. 在方差的计算公式中，数字和表示的意义分别是(    )

A. 数据的个数和平均数 B. 数据的方差和平均数
C. 数据的个数和方差 D. 以上都不对

6. 同一平面直角坐标系中，一次函数的图象与的图象如图所示，则关于的方程的解为(    )

A.  B.  C.  D. 以上都不对

7. 如图，以正方形的中心为原点建立平面直角坐标系，点的坐标为，则点的坐标为(    )

A.
B.
C.
D.

8. 某月日日，甲、乙两人的手机“微信运动”的步数统计图如图所示，则下列错误的结论是(    )

A. 日日，甲的步数逐天增加 B. 日日，乙的步数逐天减少
C. 第日，甲、乙两人的步数正好相等 D. 第日，甲的步数一定比乙的步数多

9. 下面的计算和推导导过程中，
   ，第一步
   ，第二步
   ，第三步
   ，第四步
   其中首先错误的一步是(    )

A. 第一步 B. 第二步 C. 第三步 D. 第四步

10. 如图，矩形中，，，点是边上一动点，则的最小值为(    )

A.
B.
C.
D.

11. 小风在米中长跑训练时，已跑路程米与所用时间秒之间的函数图象如图所示，下列说法错误的是(    )

A. 小风的成绩是秒
B. 小风最后冲刺阶段的速度是米秒
C. 小风第一阶段与最后冲刺阶段速度相等
D. 小风的平均速度是米秒

12. 在矩形中，、相交于点，若的面积为，则矩形的面积为(    )

A.
B.
C.
D.

13. 如图，在四边形中，对角线、相交于点，请你添加一个条件，使四边形是平行四边形，你添加的条件是(    )

A.  B.  C.  D.

14. 家乐福超市决定招聘广告策划人员一名，某应聘者三项素质测试的成绩如表：

将创新能力、综合知识和语言表达三项测试成绩按：：的比例计入总成绩，则该应聘者的总成绩是分．(    )

A.  B.  C.  D. 以上都不对

15. 如图，直角三角形纸片的一条直角边长为，斜边为，把它们按图，拼摆正方形，纸片在结合部分不重叠无缝隙，则图的中间空白部分，即四边形的面积为(    )

A.  B.  C.  D. 以上都不对

第II卷（非选择题）

二、填空题（本大题共6小题，共18.0分）

16. 已知，则的值为______．
17. 中，点，分别是的边，的中点，连接若，则______．
18. 如图，方格纸中每个最小正方形的边长为，则两平行直线、之间的距离是______ ．

19. 在平面直角坐标系中，将函数的图象向上平移个单位长度，则平移后的图象与轴的交点坐标为______．
20. 蝶几图是明朝人戈汕所作的一部组合家具的设计图“”为“蜨”，同“蝶”，它的基本组件为斜角形，包括长斜两只、右半斜两只、左半斜两只、闺一只、小三斜四只、大三斜两只，共十三只图中的“樣”和“隻”为“样”和“只”图为某蝶几设计图，其中和为“大三斜”组件“一樣二隻”的大三斜组件为两个全等的等腰直角三角形，已知某人位于点处，点与点关于直线对称，连接、若，则 ______ 度

21. 某校八年级班甲、乙两男生在次引体向上测试中有效次数如下：
    甲：，，，，；乙：，，，，；
    甲乙两同学引体向上的平均数、众数、中位数、方差如下：

根据以上信息，回答下列问题：
表格是______，______，______填数值
体育老师根据这次的成绩，决定选择甲同学代表班级参加年级引体向上比赛，选择甲的理由是______班主任李老师根据去年比赛的成绩至少次才能获奖，决定选择乙同学代表班级参加年级引体向上比赛，选择乙的理由是______．
如果乙同学再做一次引体向上，有效次数为，那么乙同学次引体向上成绩的平均数______，中位数______，方差______填“变大”、“变小”或“不变”

三、解答题（本大题共5小题，共52.0分。解答应写出文字说明，证明过程或演算步骤）

22. 
     
23. 已知一次函数的图象经过点
    求出函数的关系式．并画出其函数图象；
    直接写出该函数图象与轴的交点坐标______，与轴的交点的交点坐标______；
    利用图象说明当为何范围时，．

24. 如图，连接四边形的对角线，已知，，，，．
    求证：；
    是直角三角形．

25. 如图，在四边形中，，，对角线，交于点，平分．
    求证：；
    求证：四边形是菱形；
    如图，过点作交的延长线于点连接，若，，求的长．
     

26. 某校要印刷一批课外阅读资料，在甲印刷厂不管一次印刷多少页，每页收费元；在乙印刷厂，一次印刷页数不超过时，每页收费元；一次印刷页数超过时，超过部分每页收费元．设该校需要印刷资料的页数为，且为整数，在甲印刷厂实际付费为元，在乙印刷厂实际付费为元．
    分别求出，与的函数关系式；
    印刷页数为多少时，两家店收费一样？
    当费用不一样的时候，去哪家印刷厂比较合算？
    

答案和解析

1.【答案】 

【解析】解：、、都不是二次根式，只有符合二次根式的定义．
故选：．
根据二次根式的定义作答．
本题考查了二次根式的定义．解题的关键是掌握二次根式的定义：一般地，我们把形如的式子叫做二次根式．
 

2.【答案】 

【解析】解：，
，
四边形是平行四边形，
，
故选：．
根据平行四边形的外角的度数求得其相邻的内角的度数，然后求得其对角的度数即可．
本题主要考查了平行四边形的性质以及平角的定义，熟记平行四边形的各种性质是解题关键．
 

3.【答案】 

【解析】解：、当时，只能判定四边形是矩形，不能判定该矩形是正方形，故本选项错误；
B、矩形的四个角都是直角，则，不能判定该矩形是正方形，故本选项错误；
C、矩形的对边，不能判定该矩形是正方形，故本选项错误；
D、当矩形的对角线相互垂直，即时，该矩形是正方形，故本选项正确；
故选：．
根据有一组邻边相等或对角线互相垂直的矩形是正方形进行判断即可．
本题考查了正方形的判定．需要掌握矩形与正方形间的区别与联系．
 

4.【答案】 

【解析】解：正比例函数的图象是一条经过原点的直线，且当时，经过一、三象限．
正比例函数的大致图象是．
故选：．
正比例函数的图象是一条经过原点的直线，且当时，经过一、三象限．
此题比较简单，主要考查了正比例函数的图象特点：是一条经过原点的直线．
 

5.【答案】 

【解析】解：表示的意义是数据的个数，表示的意义是平均数，
故选：．
根据方差公式可以直接得到答案．
本题主要考查方差的定义：一般地设个数据，，，的平均数为，则方差，它反映了一组数据的波动大小，方差越大，波动性越大，反之也成立．
 

6.【答案】 

【解析】解：由函数图象，得两直线的交点坐标是，
所以，关于的方程的解为，
故选：．
根据函数图象交点的横坐标是关于的方程的解，可得答案．
本题考查了一次函数与一元一次方程，两个一次函数图象的交点的横坐标是相应方程的解．
 

7.【答案】 

【解析】解：如图所示：以正方形的中心为原点建立坐标系，点的坐标为，
点、、的坐标分别为：，，．
故选B
根据题意得：与关于轴对称，与关于轴对称，与关于原点对称，进而得出答案．
此题主要考查了关于坐标轴对称点的性质以及正方形性质，利用数形结合得出是解题关键．
 

8.【答案】 

【解析】解：日日，甲的步数逐天增加，故A中结论正确，不符合题意；
B.日日，乙的步数逐天减少，故B中结论正确，不符合题意；
C.第日，甲、乙两人的步数正好相等；故C中结论正确，不符合题意；
D.第日，甲的步数不一定比乙的步数多；故D中结论错误，符合题意；
故选：．
根据图中给出的甲乙两人这天的数据，依次判断，，，选项即可．
本题考查了折线统计图，读懂统计图，从统计图中得到必要的信息是解决问题的关键．折线统计图表示的是事物的变化情况，如增长率．
 

9.【答案】 

【解析】解：第三步错误了，应该是：．
故选：．
根据二次根式的乘法的法则进行分析即可求解．
本题主要考查二次根式的乘法，解答的关键是对二次根式的乘法的法则的掌握．
 

10.【答案】 

【解析】

【分析】
本题考查了矩形的性质，直角三角形的性质，掌握矩形的性质是本题的关键．
由矩形的性质可得，由等腰三角形的性质可求，由直角三角形的性质可求解．
【解答】
解：四边形是矩形，，
，
，
，
当时，有最小值，
，
故选A．  

11.【答案】 

【解析】解：、小风的成绩是秒，本选项正确，不符合题意；
B、小风最后冲刺阶段的速度是米秒，本选项正确，不符合题意；
C、小风第一阶段的速度是米秒，即小风第一阶段与最后冲刺阶段速度相等，本选项正确，不符合题意；
D、米秒，故本选项错误，符合题意；
故选：．
根据函数图象上的数据，求出相应阶段的速度即可得到正确的结论．
本题考查利用函数的图象解决实际问题，正确理解函数图象横纵坐标表示的意义，理解问题的过程，就能够通过图象得到函数问题的相应解决．
 

12.【答案】 

【解析】解：四边形是矩形，对角线、相交于点，
，且，
，
矩形的面积为，
故选：．
根据矩形的性质得到，推出，即可求出矩形的面积．
此题考查矩形的性质：矩形的对角线相等，且互相平分，由此可以将矩形的面积四等分，由此可以解决问题，熟记矩形的性质定理是解题的关键．
 

13.【答案】 

【解析】解：添加一个条件，使四边形是平行四边形，添加的条件是，理由如下：
，，
四边形是平行四边形，
故选：．
由平行四边形的判定方法即可得出结论．
本题考查了平行四边形的判定，熟记：对角线互相平分的四边形为平行四边形是解题的关键．
 

14.【答案】 

【解析】解：该应聘者的总成绩是：分；
故选：．
根据加权平均数的定义列式计算即可．
本题主要考查加权平均数，解题的关键是掌握加权平均数的定义．
 

15.【答案】 

【解析】解：根据图可得，，
四边形是正方形，
直角三角形纸片的一条直角边长为，斜边为，
根据勾股定理，可得直角三角形的另一直角边为，
正方形的面积为，
故选：．
根据已知可证四边形是正方形，再根据勾股定理可得正方形的边长，即可求出四边形的面积．
本题考查了正方形的性质，勾股定理等，熟练掌握正方形的性质是解题的关键．
 

16.【答案】 

【解析】解：，
，
故答案为：．
直接根据算术平方根的定义求解．
本题考查了算术平方根的定义，解题的关键是知道算术平方根和平方互为逆运算．
 

17.【答案】 

【解析】解：点、分别是的边、的中点，
，
，
，
．
故答案是：．
根据三角形的中位线定理得到，根据平行线的性质即可求得．
本题主要考查了三角形的中位线定理，能熟练地运用三角形的中位线定理是解此题的关键．
 

18.【答案】 

【解析】解：由图可知，、为小正方形的边所在直线，
，
，，
的长为个小正方形的边长，
，即两平行直线、之间的距离是．
故答案为：．
本题主要利用平行线之间的距离的定义作答．
此题很简单，考查的是两平行线之间的距离的定义，即两直线平行，则夹在两条平行线间的垂线段的长叫两平行线间的距离．
 

19.【答案】 

【解析】解：将函数的图象向上平移个单位长度的解析式为，
当时，，
平移后与轴的交点坐标为，
故答案为．
先求出该函数图象向上平移个单位后的直线解析式，再令，求出的值即可．
本题考查的是一次函数的图象与几何变换，熟知函数图象平移的规律是解答此题的关键．
 

20.【答案】 

【解析】解：点与点关于直线对称，，
，，
和为两个全等的等腰直角三角形，
，，
，
，，
，即是等腰三角形，
．
故答案为：．
由点与点关于直线对称求出，再由和求出和，进而计算出，最后利用三角形内角和即可求解．
本题考查了关于直线对称、全等三角形的性质，熟练掌握性质，找出对应边和对应角是解题的关键．
 

21.【答案】 
甲的方差较小，比较稳定 
乙的中位数是，众数是，获奖可能性大 
不变变小变小 

【解析】解：甲的成绩中，出现的次数最多，因此甲的众数是，即，
即，
将乙的成绩从小到大排列为，，，，，处在第位的数是，因此中位数是，即，
故答案为：，，．
甲的方差较小，比较稳定；乙的中位数是，众数是，获奖可能性大，
原平均数是，增加一次是，因此次的平均数还是，不变，
六次成绩排序为，，，，，，中位数是，比原来变小，方差变小，
故答案为：不变，变小，变小．
根据中位数、众数、平均数的计算方法分别计算结果，得出答案；
选择甲，主要看甲的方差较小，发挥稳定；选择乙由于乙的众数较大，中位数较大，成绩在中位数以上的占一半，获奖的可能性大；
加入一次成绩为之后，计算个数的平均数、方差、中位数，做出判断．
考查平均数、中位数、众数的意义和计算方法，明确各个统计量的意义，反映数据的特征以及计算方法是正确解答的关键．
 

22.【答案】解：原式；

原式
；

原式

；

原式． 

【解析】直接利用二次根式的加减运算法则计算得出答案；
直接利用平方差公式计算得出答案；
直接化简二次根式，再利用二次根式的混合运算法则计算得出答案；
直接化简二次根式，进而利用二次根式的混合运算法则计算得出答案．
此题主要考查了二次根式的混合运算，正确掌握相关运算法则是解题关键．
 

23.【答案】   

【解析】解：把代入，
得，解得，
所以一次函数解析式为，
如图，

当时，，
解得，
则该函数图象与轴的交点坐标为，
当时，，
则该函数图象与轴的交点坐标为．
故答案为：，；
根据图象可得，当时，．
把已知点的坐标代入中求出得到一次函数解析式，过点，画直线，得到函数图象；
利用坐标轴上点的坐标特征即可求出与轴、轴的交点坐标；
结合函数图象，写出一次函数图象不在轴下方所对应的自变量的范围即可．
本题考查了待定系数法求一次函数解析式：先设出函数的一般形式，如求一次函数的解析式时，先设；再将自变量的值及与它对应的函数值的值代入所设的解析式，得到关于待定系数的方程或方程组；然后解方程或方程组，求出待定系数的值，进而写出函数解析式．也考查了一次函数图象．
 

24.【答案】证明：，，，
，
，
；
，，，
，
是直角三角形． 

【解析】根据勾股定理得出，即可求解；
进而利用勾股定理的逆定理解答即可．
此题考查勾股定理，关键是根据勾股定理得出，进而利用勾股定理的逆定理解答．
 

25.【答案】证明：，
，
平分，
，
；
证明：，，
，
，
四边形是平行四边形，
，
平行四边形是菱形；
解：四边形是菱形，
，，，
，
，
，
，
在中，，，
，
． 

【解析】先判断出，进而判断出；
根据，，得出，即可得出结论；
先判断出，再求出，利用勾股定理求出，即可得出结论．
此题主要考查了菱形的判定和性质，平行四边形的判定和性质，角平分线的定义，勾股定理，判断出是解本题的关键．
 

26.【答案】解：根据题意得：，
，
答：，；
由得：，
印刷页数为时，两家店收费一样；
当时，
解得：，
时，到甲印刷厂比较合算；
当时，
解得：，
时，到乙印刷厂比较合算；
综上所述，时，到甲印刷厂比较合算；时，到乙印刷厂比较合算． 

【解析】根据题意得：，；
由得印刷页数为时，两家店收费一样；
分两种情况：当，即时，到甲印刷厂比较合算；当，即时，到乙印刷厂比较合算．
本题考查一次函数的应用，解题的关键是读懂题意，列出函数关系式．