
2021-2022学年吉林省松原市乾安县八年级(下)期末数学试卷(Word解析版)
展开绝密★启用前
2021-2022学年吉林省松原市乾安县八年级(下)期末数学试卷
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上,写在试卷上无效。
3.考试结束后,本试卷和答题卡一并交回。
一、选择题(本题共6小题,共12分)
- 下列运算正确的是( )
A. B.
C. D.
- 下列四组数,可作为直角三角形三边的是( )
A. ,, B. ,,
C. ,, D. ,
- 不能判定四边形为平行四边形的题设是( )
A. ,
B. ,
C. ,
D. ,
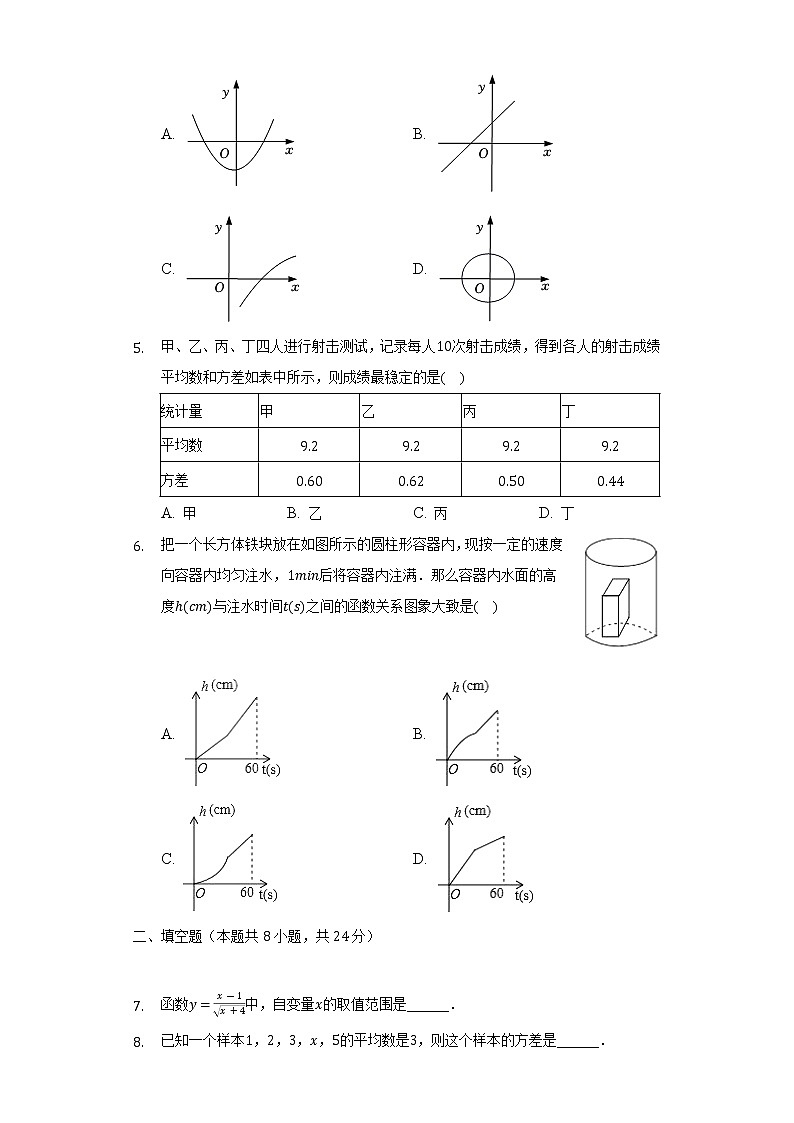
- 下列表示与之间的关系的图象中,不是的函数的是( )
A. B.
C. D.
- 甲、乙、丙、丁四人进行射击测试,记录每人次射击成绩,得到各人的射击成绩平均数和方差如表中所示,则成绩最稳定的是( )
统计量 | 甲 | 乙 | 丙 | 丁 |
平均数 | ||||
方差 |
A. 甲 B. 乙 C. 丙 D. 丁
- 把一个长方体铁块放在如图所示的圆柱形容器内,现按一定的速度向容器内均匀注水,后将容器内注满.那么容器内水面的高度与注水时间之间的函数关系图象大致是( )
A. B.
C. D.
二、填空题(本题共8小题,共24分)
- 函数中,自变量的取值范围是______.
- 已知一个样本,,,,的平均数是,则这个样本的方差是______.
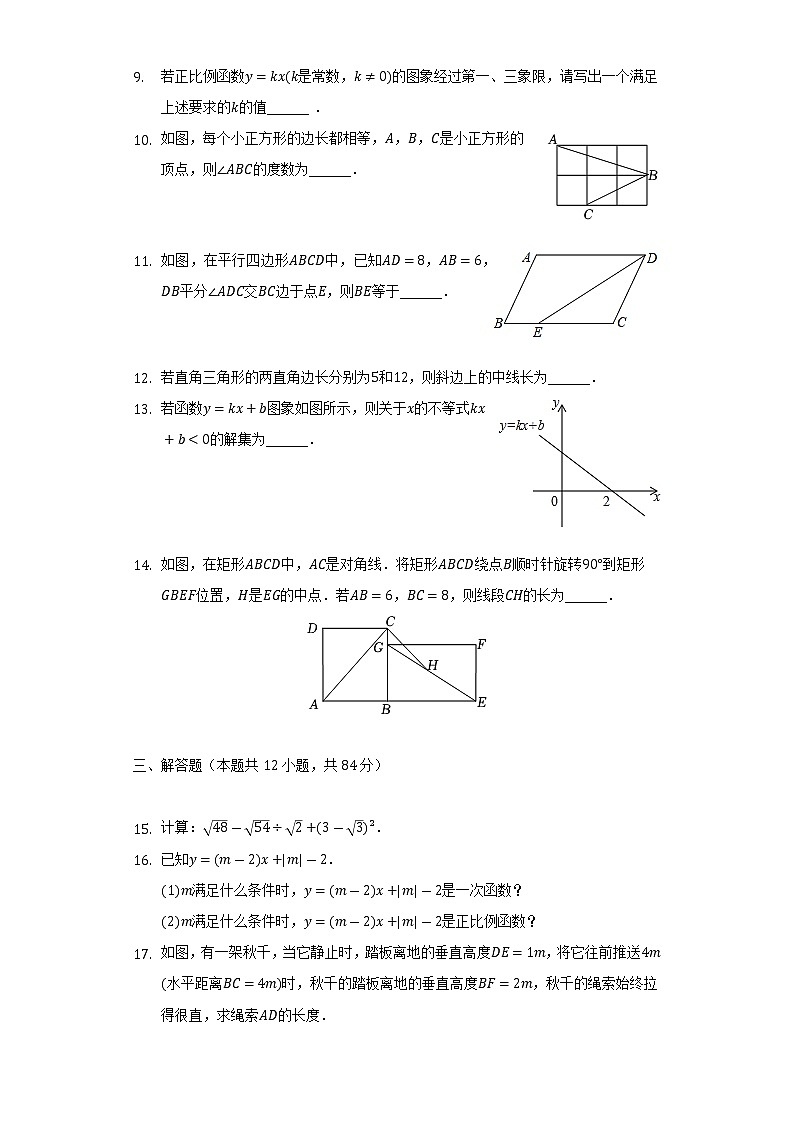
- 若正比例函数是常数,的图象经过第一、三象限,请写出一个满足上述要求的的值______ .
- 如图,每个小正方形的边长都相等,,,是小正方形的顶点,则的度数为______.
- 如图,在平行四边形中,已知,,平分交边于点,则等于______.
- 若直角三角形的两直角边长分别为和,则斜边上的中线长为______.
- 若函数图象如图所示,则关于的不等式的解集为______.
- 如图,在矩形中,是对角线.将矩形绕点顺时针旋转到矩形位置,是的中点.若,,则线段的长为______.
三、解答题(本题共12小题,共84分)
- 计算:.
- 已知.
满足什么条件时,是一次函数?
满足什么条件时,是正比例函数? - 如图,有一架秋千,当它静止时,踏板离地的垂直高度,将它往前推送水平距离时,秋千的踏板离地的垂直高度,秋千的绳索始终拉得很直,求绳索的长度.
- 如图,在平行四边形中,点、分别在、上,且,求证:.
- 如图,网格中有一条线段,点、都在格点上,网格中的每个小正方形的边长为请在图和图中各画出一个格点,使是直角三角形,且,并满足以下要求:
在图中画出的三角形的两条直角边的长度均为有理数画出一个即可.
在图中画出的三角形的两条直角边的长度均为无理数画出一个即可.
满足、的共有______ 个
- 已知矩形中,对角线与相交于点分别过点、作、的平行线交于点.
求证:四边形为菱形.
若,,求菱形的面积.
- 为了推动阳光体育运动的广泛开展,引导学生走向操场,走进大自然,走到阳光下,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了如下的统计图和图,请根据相关信息,解答下列问题:
Ⅰ本次接受随机抽样调查的学生人数为______,图中的值为______;
Ⅱ求本次调查获取的样本数据的众数和中位数;
Ⅲ根据样本数据,若学校计划购买双运动鞋,建议购买号运动鞋多少双? - 直线经过点,交轴于点直线交轴于点,且与直线相交于点.
求点的坐标;
求的面积. - 甲骑摩托车从地去地,乙开汽车从地去地,同时出发,匀速行驶,各自到达终点后停止,甲、乙两人之间的距离为与甲行驶的时间为之间的关系如图所示.
以下是点、点、点所代表的实际意义,请将,,填对应的横线上:
甲到达终点______;
甲、乙两人相遇______;
乙到达终点______;
、两地之间的路程为______千米;
求甲、乙各自的速度;
求甲出发多长时间后,甲、乙两人相距千米.
- 如图,在边长为的正方形中,是边的中点,将沿对折至,延长交于点,连接.
求证:≌;
求的长.
- 小明到服装店参加社会实践活动,服装店经理让小明帮助解决以下问题:
服装店准备购进甲乙两种服装,甲种每件进价元,售价元;乙种每件进价元,售价元.计划购进两种服装共件,其中甲种服装不少于件.
若购进这件服装的费用不得超过,则甲种服装最多购进多少件?
在的条件下,该服装店在月日“父亲节”当天对甲种服装以每件优惠元的价格进行优惠促销活动,乙种服装价格不变,那么该服装店应如何调整进货方案才能获得最大利润? - 如图,直线分别与轴、轴交于点、点,点的坐标为,为直线上一动点,连接交轴于点.
点的坐标为______,不等式的解集为______;
若,求点的坐标;
如图,以为边作菱形,且,连接、、,求证:≌.
答案和解析
1.【答案】
【解析】解:.,故此选项不合题意;
B.,故此选项不合题意;
C.,故此选项不合题意;
D.,故此选项符合题意;
故选:.
直接利用二次根式的混合运算法则分别计算,进而判断得出答案.
此题主要考查了二次根式的混合运算,正确掌握相关运算法则是解题关键.
2.【答案】
【解析】解:、,故不是直角三角形,不符合题意;
B、,故不是直角三角形,不符合题意;
C、,故不是直角三角形,不符合题意;
D、,故是直角三角形,符合题意.
故选:.
先求出两小边的平方和,再求出最长边的平方,最后看看是否相等即可.
此题主要考查了勾股定理逆定理,关键是掌握如果三角形的三边长,,满足,那么这个三角形就是直角三角形.
3.【答案】
【解析】解:,,
四边形为平行四边形两组对边分别相等的四边形是平行四边形;
故本选项能判定四边形为平行四边形.
B.,不能判定四边形为平行四边形,
故此选项符合题意;
C.,,
四边形为平行四边形对角线互相平分的四边形是平行四边形;
故本选项能判定四边形为平行四边形;
D.,,
四边形为平行四边形两组对角分别相等的四边形是平行四边形;
故本选项能判定四边形为平行四边形;
故选:.
根据平行四边形的判定定理:两组对边分别相等的四边形是平行四边形,两组对角分别相等的四边形是平行四边形,对角线互相平分的四边形是平行四边形,两组对边分别平行的四边形是平行四边形,一组对边平行且相等的四边形是平行四边形进行分析即可.
此题主要考查了平行四边形的判定,熟练掌握并运用平行四边形的判定定理是解题关键.
4.【答案】
【解析】解:选项A,,所画图象中,对于自变量的每一个确定值,都有唯一的确定值与其对应,而选项D所画图象中,对于部分自变量的确定值,都有不唯一的确定值与其对应,
选项A,,所画图象中,是的函数,选项D所画图象中,不是的函数,
选项A,,不符合题意,选项D符合题意,
故选:.
根据函数的概念进行辨别即可.
此题考查了对函数概念的理解能力,关键是能准确运用数形结合理解该知识.
5.【答案】
【解析】解:每人次射击成绩的平均数均是环,方差依次为、、、,
丁的方差最小,
成绩最稳定的是丁;
故选D.
根据方差的意义可作出判断.方差是用来衡量一组数据波动大小的量,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
本题考查方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
6.【答案】
【解析】解:根据题意可知,按一定的速度向容器内均匀注水,
所以函数图像均为匀速上升,
由此可排除,选项,
刚开始时由于长方体铁块在圆柱体容器内,
注水部分的底面积为圆柱体容器的底面积减去长方体的底面积,
所以水面以较快速度均匀上升,
当水淹没长方体铁块后一直到水注满容器,
底面积是圆柱体的底面积,
所以水面以较慢速度均匀上升,
所以排除选项,选项D符合题意,
故选:.
根据题意可知,在注满水的过程中,水面均是匀速上升,下面部分的底面积小于上面部分,所以水面上升速度较快,由此可得出答案.
本题考查函数图象的意义,深刻理解实际问题中函数图象所代表的意义,是快速解出这道题的关键.
7.【答案】
【解析】解:由题意得:,
解得:,
故答案为:.
根据二次根式的被开方数是非负数、分母不为列出不等式,解不等式得到答案.
本题考查的是函数自变量的取值范围的确定,掌握二次根式的被开方数是非负数、分母不为是解题的关键.
8.【答案】
【解析】解:,,,,,它的平均数是,
,
,
;
这个样本的方差是;
故答案为:.
先由平均数公式求得的值,再由方差公式求解即可.
本题考查了平均数和方差:一般地设个数据,,,的平均数为,则方差,它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
9.【答案】
【解析】解:时直线经过一、三象限,
即可.
故答案为:满足即可.
正比例函数是常数,的图象经过第一、三象限,即可,时图象经过二、四象限.
本题考查正比例函数的性质,解题关键是掌握与直线的变化规律.
10.【答案】
【解析】解:如图,连接.
由题意,,,,
,,
是等腰直角三角形,且,
,
故答案为:.
根据勾股定理得到,,的长度,再判断是等腰直角三角形,进而得出结论.
本题考查了勾股定理及其逆定理,等腰直角三角形的判定与性质,判断出是等腰直角三角形是解决本题的关键.
11.【答案】
【解析】解:根据平行四边形的性质得,
,
又平分,
,
,
,
即.
故答案为:.
由平行四边形对边平行根据两直线平行,内错角相等可得,而平分,进一步推出,在同一三角形中,根据等角对等边得,则可求解.
本题考查通过平行四边形性质的应用,及等腰三角形的判定,属于基础题.
12.【答案】
【解析】解:直角三角形两直角边长为和,
斜边,
此直角三角形斜边上的中线的长.
故答案为:.
根据勾股定理可求得直角三角形斜边的长,再根据直角三角形斜边上的中线等于斜边的一半即可求解.
此题主要考查勾股定理及直角三角形斜边上的中线的性质;熟练掌握勾股定理,熟记直角三角形斜边上的中线的性质是解决问题的关键.
13.【答案】
【解析】解:从图象知,函数的图象经过点,并且函数值随的增大而减小,
当是,,
即关于的不等式的解集是.
故答案为.
从图象得到函数的增减性及与轴的交点的横坐标,即能求得不等式的解集.
本题考查了一次函数与不等式组的关系及数形结合思想的应用.解决此类问题关键是仔细观察图形,注意几个关键点交点、原点等,做到数形结合.
14.【答案】
【解析】解:过点作于点,
将绕点顺时针旋转到位置,,,
,,,
,
是的中点,
,,
,
在中,.
故答案为:.
首先过点作于点,由将绕点顺时针旋转到位置,,,可得,,,又由是的中点,易得是的中位线,继而求得与的长,由勾股定理即可求得线段的长.
此题考查了旋转的性质、矩形的性质、三角形中位线的性质以及勾股定理.此题难度适中,注意掌握辅助线的作法,注意掌握旋转前后图形的对应关系,注意掌握数形结合思想的应用.
15.【答案】解:原式
.
【解析】先根据二次根式的除法法则和完全平方公式计算,然后化简后合并即可.
本题考查了二次根式的混合运算,熟练掌握二次根式的性质、二次根式的除法法则和完全平方公式是解决问题的关键.
16.【答案】解:由题意得:,
解得:;
由题意得:,且,
解得:.
【解析】利用一次函数定义可得,再解不等式即可;
利用正比例函数定义可得:,且,再解方程可得的值.
此题主要考查了正比例函数和一次函数定义,关键是掌握形如是常数,的函数叫做正比例函数.
17.【答案】解:在中,
,
设秋千的绳索长为,则,
故,
解得:,
答:绳索的长度是.
【解析】设秋千的绳索长为,根据题意可得,利用勾股定理可得.
此题主要考查了勾股定理的应用,关键是正确理解题意,表示出、的长,掌握直角三角形中两直角边的平方和等于斜边的平方.
18.【答案】证明:四边形是平行四边形,
,,
在和中
≌,
.
【解析】根据平行四边形性质得出,,根据全等三角形的判定得出≌,即可得出答案.
本题考查了平行四边形的性质和全等三角形的判定,能求出≌是解此题的关键.
19.【答案】
【解析】解:点的位置如图所示.
点的位置如图所示.
满足条件的三角形有个.
故答案为:.
根据要求作出图形即可,有两种情形.
根据要求作出图形即可,有四种情形.
根据可得结论.
本题考查作图应用与设计作图,无理数,直角三角形等知识,解题的关键是学会利用数形结合的思想解决问题,属于中考常考题型.
20.【答案】结论:四边形的形状是菱形,
证明:,,
四边形是平行四边形,
四边形是矩形,
,,,
,
四边形是菱形;
解:,,
矩形的面积,
,
四边形的面积.
【解析】首先由,,可证得四边形是平行四边形,又由四边形是矩形,根据矩形的性质,易得,即可判定四边形是菱形,
由矩形的性质可知四边形的面积为矩形面积的一半,问题得解.
本题考查了菱形的判定与性质、矩形的性质等知识,熟练掌握菱形的判定是解决问题的关键,记住矩形的对角线把矩形分成面积相等的个三角形,属于中考常考题型.
21.【答案】解:Ⅰ;;
Ⅱ在这组样本数据中,出现了次,出现次数最多,
这组样本数据的众数为;
将这组样本数据从小到大得顺序排列,其中处于中间的两个数都为,
中位数为;
Ⅲ在名学生中,鞋号为的学生人数比例为,
由样本数据,估计学校各年级中学生鞋号为的人数比例约为,
则计划购买双运动鞋,有双为号.
【解析】解:Ⅰ本次接受随机抽样调查的学生人数为,图中的值为;
故答案为:;;
Ⅱ见答案;
Ⅲ见答案.
Ⅰ根据条形统计图求出总人数即可;由扇形统计图以及单位,求出的值即可;
Ⅱ找出出现次数最多的即为众数,将数据按照从小到大顺序排列,求出中位数即可;
Ⅲ根据题意列出算式,计算即可得到结果.
此题考查了条形统计图,扇形统计图,以及用样本估计总体,弄清题意是解本题的关键.
22.【答案】解:直线经过点,
,解得,
此直线解析式为,
直线交轴于点,
,
此直线解析式为,
,
解得,
点;
把代入,得,
,
,
,
的面积.
【解析】首先将已知点的坐标代入到一次函数的解析式求得值和值,然后解析式联立成方程组,解方程组即可求得交点的坐标;
先求得的坐标,即可求得,然后利用三角形的面积公式即可求得.
本题考查了两条直线平行或相交的问题,解题的关键是求得两直线的解析式及交点坐标,难度不大.
23.【答案】
【解析】解:分析函数图象知出发小时时,甲乙在途中相遇;出发小时时乙到达地;小时时甲到达地,
故答案为:;;;
根据函数图象可得,、两地之间路程为千米,
故答案为:;
甲的速度是:千米时,则乙的速度是:千米时;
相遇之前:小时,
相遇之后:小时,
即甲出发小时或小时后,甲、乙两人相距千米.
根据函数图象和图象中的数据可以解答本题;
由图象可得,、两地之间路程为千米;
出发小时时,甲乙在途中相遇,从而可以求得它们各自的速度;
根据图象可知相遇前和相遇后,存在这两种情况甲、乙两人相距千米,然后列式计算即可.
本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用函数的思想和数形结合的思想解答.
24.【答案】证明:在正方形中,,,
将沿对折至,
,,,
,,
又,
在和中,
,
≌;
解:≌,
,
设,则,
为的中点,
,
,
在中,,解得,
.
【解析】此题主要考查了勾股定理的综合应用以及翻折变换的性质,根据翻折变换的性质得出对应线段相等是解题关键.
首先证明,然后再证明,接下来,依据可证明≌;
利用勾股定理得出,进而求出即可.
25.【答案】解:设购进甲种服装件,由题意可知:
,解得:.
答:甲种服装最多购进件.
设总利润为元,因为甲种服装不少于件,所以,
,
方案:当时,,随的增大而增大,
所以当时,有最大值,则购进甲种服装件,乙种服装件;
方案:当时,所有方案获利相同,所以按哪种方案进货都可以;
方案:当时,,随的增大而减少,
所以当时,有最大值,则购进甲种服装件,乙种服装件.
【解析】设购进甲种服装件,根据题意列出关于的一元一次不等式,解不等式得出结论;
找出利润关于购进甲种服装之间的关系式,分的情况讨论.
本题考查了一次函数的应用与解一元一次不等式,解题的关键是:根据题意列出关于的一元一次不等式;找出利润关于购进甲种服装的关系式,由函数的性质分的情况讨论.本题属于中档题,难度不大,需要分的情况讨论.
26.【答案】
【解析】解:,
当时,有,
解得:,
点的坐标为.
观察函数图象,可知:当时,直线在轴上方,
不等式的解集为.
故答案为:;;
解:当时,,
点的坐标为
,
,即,
.
当时,有,
解得:,
点的坐标为;
证明:四边形是菱形,
,
,
为等边三角形,
,,
,,
,
为等边三角形,
,
,
,
≌.
先确定出点的坐标,借助图象即可得出结论;
先确定出点的坐标为,再判断出,进而求出点的纵坐标,即可得出结论;
先判断出、为等边三角形,根据等边三角形的性质得,,,,可得,利用即可得出结论.
此题是一次函数综合题,主要考查了一次函数与不等式,三角形的面积公式,菱形的性质,等边三角形的判定和性质,全等三角形的判定和性质,利用数形结合的思想是解本题的关键.
2023-2024学年吉林省松原市乾安县八年级(上)期末数学试卷(含详细答案解析): 这是一份2023-2024学年吉林省松原市乾安县八年级(上)期末数学试卷(含详细答案解析),共19页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
2023-2024学年吉林省松原市乾安县八年级(上)期末数学试卷(含解析): 这是一份2023-2024学年吉林省松原市乾安县八年级(上)期末数学试卷(含解析),共19页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
2022-2023学年吉林省松原市乾安县八年级(上)期中数学试卷(解析版): 这是一份2022-2023学年吉林省松原市乾安县八年级(上)期中数学试卷(解析版),共25页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












