还剩15页未读，继续阅读

下载需要20学贝 1学贝=0.1元

使用下载券免费下载

加入资料篮

立即下载

2021-2022学年广西钦州市七年级（下）期末数学试卷（Word解析版）

展开

这是一份2021-2022学年广西钦州市七年级（下）期末数学试卷（Word解析版），共18页。试卷主要包含了5尺，【答案】D，【答案】B，【答案】C等内容，欢迎下载使用。

绝密★启用前

2021-2022学年广西钦州市七年级（下）期末数学试卷

注意事项:
1.答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案写在答题卡上，写在试卷上无效。
3.考试结束后，本试卷和答题卡一并交回。

第I卷（选择题）

一、选择题（本大题共12小题，共36分。在每小题列出的选项中，选出符合题目的一项）

下列实数中，是无理数的为( )

A. B. C. D.

如图，，已知，则的度数是( )

A.
B.
C.
D.

下列调查中，适宜采用全面调查的是( )

A. 检测“天舟四号”货运飞船的零部件 B. 调查某批次汽车的抗撞击能力
C. 了解我市小学生睡眠时间 D. 了解全国中学生视力情况

在平面直角坐标系的第二象限内有一点，它到轴的距离为，到轴的距离为，则点的坐标为( )

A. B. C. D.

一个关于的一元一次不等式组的解集在数轴上的表示如图所示，则该不等式组的解集是( )

A. B. C. D. 无解

方程有个正整数解．( )

A. B. C. D. 无数

若将三个数，，表示在数轴上，其中能被如图所示的墨迹覆盖的数是( )

A. B. C. D. 和

若，则下列不等式中，不成立的是( )

A. B. C. D.

一个瓶子中装有一些豆子，从瓶子中取出粒豆子做上标记，然后放回瓶子充分拥匀后，再取出粒豆子，发现带标记的豆子有粒，则估计瓶子中豆子的粒数为( )

A. B. C. D.

如图，直线，，相交于点，已知平分，若：：，则的度数为( )

A.
B.
C.
D.

孙子算经中有一道题：“今有木，不知长短，引绳度之，余绳四尺五寸：屈绳量之，不足一尺，木长几何？”意思是：“用一根绳子去量一根木条的长，绳子还剩余尺：将绳子对折再量木条，则木条还剩余尺，问木条长多少尺？”现设木条长尺，绳子长尺，则可列方程组为( )

A. B.
C. D.

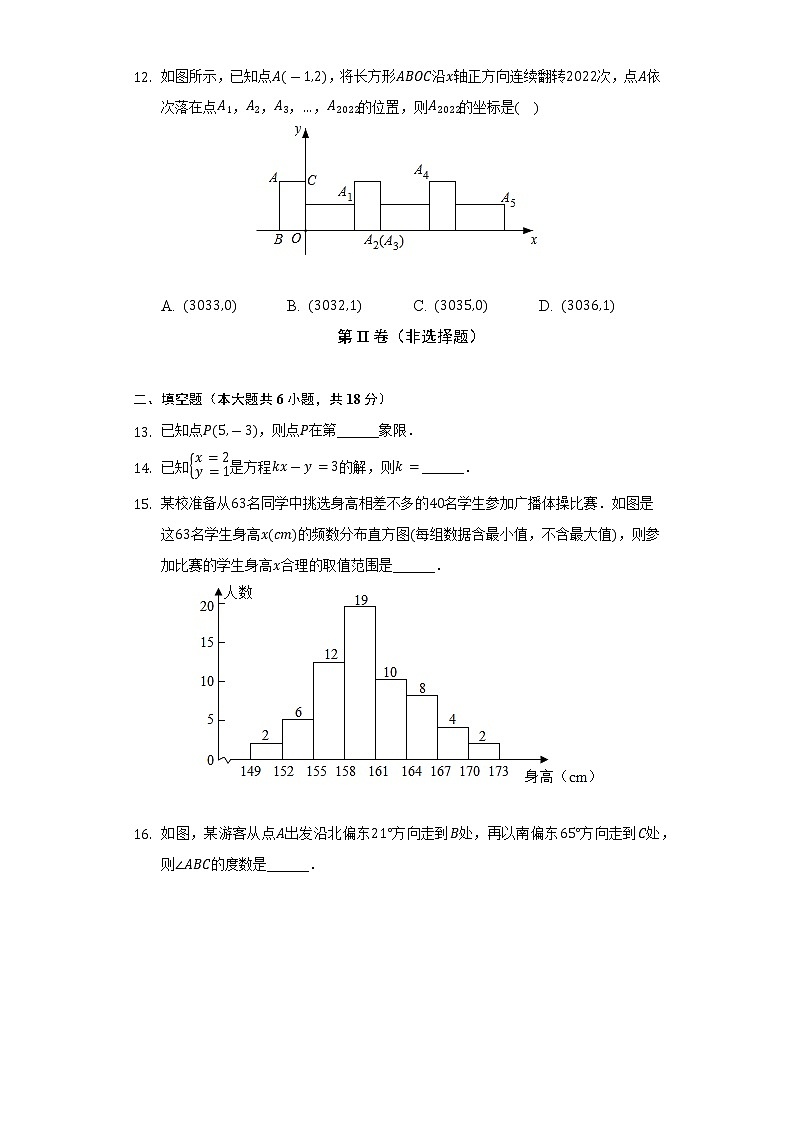
如图所示，已知点，将长方形沿轴正方向连续翻转次，点依次落在点，，，，的位置，则的坐标是( )

A. B. C. D.

第II卷（非选择题）

二、填空题（本大题共6小题，共18分）

已知点，则点在第______象限．
已知是方程的解，则______．
某校准备从名同学中挑选身高相差不多的名学生参加广播体操比赛．如图是这名学生身高的频数分布直方图每组数据含最小值，不含最大值，则参加比赛的学生身高合理的取值范围是______．

如图，某游客从点出发沿北偏东方向走到处，再以南偏东方向走到处，则的度数是______．

由，，能确定是两位数，请确定是______位数．
代数式的最大值为______．

三、解答题（本大题共8小题，共66分。解答应写出文字说明，证明过程或演算步骤）

本小题分
计算：．
本小题分
解方程组
本小题分
解不等式组：并利用数轴确定不等式组的解集．
本小题分
为了解男生报考体育测试项目的意向，某校从九年级各班男生中随机抽取若干人组成调查样本，根据收集到的数据整理并绘制出以下不完整的条形统计图和扇形统计图．请根据信息解答问题．

项目	男生体育测试项目
类	米	分钟跳绳	立定跳远
类	米	立宝跳远	实心球
类	米	实心球	分钟跳绳

请直接写出此次调查样本的容量大小和类项目所对应圆心角的度数；
请补充完整图中的条形统计图；
该校九年级男生共名，请估计九年级报考类项目的男生人数．

本小题分
如图是边长为的小正方形拼成的网格，将经过平移后得，图中标出了点的对应点利用网格点和直尺，完成下列各题：
补全；
连接，，请写出与的位置与数量关系；
若点，点，请直接写出点的坐标．

本小题分
如图，直线，被直线所截，连接，，已知，．
若，求的度数；
判断与的位置关系，并说明理由；
若平分，求证：平分．

本小题分
习近平总书记说“读书可以让人保持想活力，让人得到智慧启发，让人滋养浩然之气”某校为提高学生的阅读品味，现决定购买获得十届茅盾文学奖的北上徐则臣著和牵风记徐怀中著两种书．若购买本北上和本牵风记需用元；购买本北上与购买本牵风记的费用相同．
求每本北上和每本牵风记各为多少元；
该校决定购买以上两种书共本，总费用不超过元，那么该校最多可以购多少本北上．
本小题分
如图，在平直角坐标系中，线段的两端点坐标分别是，，线段与轴交于点，把线段平移，使点的对应点落在轴正半轴上．
若点，请直接写出点的对应点的坐标．
连接，，请求出的面积？
连接和，记点，的面积为，若，求的取值范围．

答案和解析

1.【答案】

【解析】解：，
，，是有理数；
是无理数，
故选：．
无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．
此题主要考查了无理数的定义，其中初中范围内学习的无理数有：，等；开方开不尽的数；以及像，等有这样规律的数．

2.【答案】

【解析】解：，，
，
，
故选：．
两直线平行，同旁内角互补，据此进行解答．
本题考查了平行线的性质．注意两直线平行，同旁内角互补．

3.【答案】

【解析】解：检测“天舟四号”货运飞船的零部件，适合进行普查，故本选项符合题意；
B.调查某批次汽车的抗撞击能力，适合进行抽样调查，故本选项不合题意；
C.了解我市小学生睡眠时间，适合进行抽样调查，故本选项不合题意；
D.了解全国中学生视力情况，适合进行抽样调查，故本选项不合题意；
故选：．
根据普查得到的调查结果比较准确，但所费人力、物力和时间较多，而抽样调查得到的调查结果比较近似解答．
本题考查的是抽样调查和全面调查的区别，选择普查还是抽样调查要根据所要考查的对象的特征灵活选用，一般来说，对于具有破坏性的调查、无法进行普查、普查的意义或价值不大，应选择抽样调查，对于精确度要求高的调查，事关重大的调查往往选用普查．

4.【答案】

【解析】解：由题意，得：
，．
又在第二象限内有一点，
，，
点的坐标为，
故选：．
根据各象限内点的坐标特征，可得答案．
本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限；第二象限；第三象限；第四象限．

5.【答案】

【解析】解：根据数轴可知：两不等式的解集没有公共部分，
所以该不等式组无解，
故选：．
根据数轴得出两不等式的解集没有公共部分，再求出组成的不等式组的解集即可．
本题考查了在数轴上表示不等式的解集，解一元一次不等式组等知识点，能根据数轴得出正确信息是解此题的关键，注意：同大取大，同小取小，大小小大取中间，大大小小解不了．

6.【答案】

【解析】

【解答】
解：，当时，；
当时，；
当时，，
则方程的正整数解是：，共有个．
故选B．
【分析】
把方程变形成，然后给正整数值，进而确定的值，即可得到正整数解．
本题考查了方程的正整数解，理解方程的解的定义是关键．

7.【答案】

【解析】解：，，，
三个数，，只有被墨迹覆盖，
故选：．
逐一确定，，各在数轴上的大体位置进行确定结果．
此题考查了用数轴表示实数的能力，关键是能运用平方根的知识准确确定各数的范围．

8.【答案】

【解析】解：、，，故本选项成立；
B、，，故本选项不成立；
C、，，故本选项成立；
D、，，故本选项成立．
故选：．
根据不等式的基本性质对各选项进行逐一分析即可．
本题考查的是不等式的性质，熟知不等式的两边同时乘以或除以同一个负数，不等号的方向改变是解答此题的关键．

9.【答案】

【解析】解：设瓶子中有豆子粒，
根据题意得：，
解得：，
经检验：是原分式方程的解，
答：估计瓶子中豆子的数量约为粒．
故选：．
设瓶子中有豆子粒，根据取出粒刚好有记号的粒列出算式，再进行计算即可．
本题考查了用样本的数据特征来估计总体的数据特征，利用样本中的数据对整体进行估算是统计学中最常用的估算方法．

10.【答案】

【解析】解：直线，，相交于点，：：，
，，
，
解得：，
平分，
，
．
故选：．
由邻补角的定义可得，从而可求得，再由角平分线的定义求得，利用对顶角相等即得的度数．
本题主要考查对顶角、邻补角，角平分线的定义，解答的关键是结合图形分析清楚角之间的关系．

11.【答案】

【解析】解：现设木条长尺，绳子长尺，则可列方程组为：．
故选：．
直接利用“绳长木条；木条绳子”分别得出等式求出答案．
此题主要考查了由实际问题抽象出二元一次方程组，正确得出等量关系是解题关键．

12.【答案】

【解析】解：根据图形分析，从开始旋转，当旋转到时，回到矩形的起始位置，所以为一个循环，故坐标变换规律为次一循环．
，，，，
，，，，
，，，，
，，，，
当时，即，解得，
横坐标为，纵坐标为，
则的坐标，
故选：．
分析，，，，点坐标，找到规律求解．
本题主要考查图形的旋转变换，解题关键是找到图形在旋转的过程中，点坐标变化规律进而求解．

13.【答案】四

【解析】解：点的横坐标大于，纵坐标小于，
点在第四象限．
故答案为：四．
根据各象限内点的坐标符号可得其所在象限．
本题主要考查点的坐标，解题的关键是掌握四个象限内点的坐标符号特点．

14.【答案】

【解析】解：把代入方程，
得，
解得．
知道了方程的解，可以把这对数值代入方程，得到一个含有未知数的一元一次方程，从而可以求出的值．
解题关键是把方程的解代入原方程，使原方程转化为以系数为未知数的方程．
一组数是方程的解，那么它一定满足这个方程，利用方程的解的定义可以求方程中其他字母的值．

15.【答案】

【解析】解：抽取人，比较整齐，因此是相邻几组的频数之和为，而的人数为人，
因此比较合适，
故答案为：．
根据频数分布直方图中各组的频数，结合所抽取的相邻几组的频数之和为即可得出答案．
本题考查频数分布直方图，理解频数分布直方图中数据的意义及相互关系是正确判断的前提．

16.【答案】

【解析】解：如图：

由题意得：
，，，
，
，
故答案为：．
根据题意可得，，，从而利用平行线的性质可得，然后进行计算即可解答．
本题考查了方向角，熟练掌握方向角的定义即可解答．

17.【答案】两

【解析】解：，，，
是两位数．
故答案为：两．
根据，可知，，故能确定是两位数，而，故是两位数．
本题考查立方根，理解题干中所提供的计算方法是得出正确答案的关键．

18.【答案】

【解析】解：当，时，即，；
当，时，无解；
当，时，即，．
当，时，即，．
所以最大值是．
解法二：就是数轴到的距离等于就是到的距离．那么最大的时候是离最远离最近的时候也就是的时候，
所以的最大值为．
求这个式子的范围，可以根据对的值的范围的讨论，去掉绝对值符号，对式子进行化简．
此题考查绝对值的化简，利用分类讨论的方法，把的取值分为多段，去掉绝对值符号．

19.【答案】解：

．

【解析】先化简各式，然后再进行计算即可解答．
本题考查了实数的运算，准确熟练地化简各式是解题的关键．

20.【答案】解：，
得：，
解得：，
把代入得：，
解得：，
故方程组的解为．

【解析】直接利用加减消元法解方程得出答案．
此题主要考查了解二元一次方程组，正确掌握解方程组的方法是解题关键．

21.【答案】解：解不等式，得：，
解不等式，得：，
将不等式解集表示在数轴上如下：

则不等式组的解集为．

【解析】分别求出每一个不等式的解集，在数轴上表示出不等式的解集，继而得出答案．
本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．

22.【答案】解：被调查的样本容量是：，
类项目所对应圆心角的度数为：；
类人数：人，
补全条形统计图如下：

类所占百分比：，
人，
答：估计九年级报考类项目的男生人数为人．

【解析】根据类的人数人占总体的进行计算样本总人数，再用乘类项目所占比例即可得出类项目所对应圆心角的度数；
根据中所求数据，即可得出类人数，进而补全条形统计图；
根据中的数据即可估计名初三男生中报考类的男生人数．
此题考查条形统计图、扇形统计图以及样本估计总体的统计思想，理清统计图中各个数据之间的关系是解决问题的关键．

23.【答案】解：补全如图所示；

由图形可知与的位置与数量关系分别为：平行且相等；
若点，点，则点的坐标为，即．

【解析】根据平移的性质找出对应点即可求解；
由图形可直接得出答案；
由点到点的平移变换规律即可求解．
本题考查了平移变换的性质，熟练掌握平移变换的性质是解题的关键．

24.【答案】解：，
，
又，
；
解：．
理由：，
，
又，
，
；
证明：，
，
，
，
平分，
，
，
平分．

【解析】由平行线的性质求得，然后由邻补角的定义求得的度数即可；
由平行线的性质可知：，然后由，再证得，从而可证得；
由可证明，由，可证明，由角平分线的定义可知，，从而可证明．
本题主要考查的是平行线的性质的应用，掌握平行线的性质是解题的关键．

25.【答案】解：设每本北上的价格为元，每本牵风记的价格为元，
依题意得：，
解得：．
答：每本北上的价格为元，每本牵风记的价格为元．
设该校可以购买本北上，则可以购买本牵风记，
依题意得：，
解得：．
答：该校最多可以购买本北上．

【解析】设每本北上的价格为元，每本牵风记的价格为元，根据“购买本北上和本牵风记需用元；购买本北上与购买本牵风记的费用相同”，即可得出关于，的二元一次方程组，解之即可得出每本北上和每本牵风记的价格；
设该校可以购买本北上，则可以购买本牵风记，利用总价单价数量，结合总价不超过元，即可得出关于的一元一次不等式，解之取其中的最大值即可得出北上的最大购买量．
本题考查了二元一次方程组的应用以及一元一次不等式的应用，解题的关键是：找准等量关系，正确列出二元一次方程组；根据各数量之间的关系，正确列出一元一次不等式．