

2021-2022学年陕西省渭南市华州区七年级(下)期末数学试卷-(Word解析版)
展开绝密★启用前
2021-2022学年陕西省渭南市华州区七年级(下)期末数学试卷
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上,写在试卷上无效。
3.考试结束后,本试卷和答题卡一并交回。
第I卷(选择题)
一、选择题(本大题共8小题,共24.0分。在每小题列出的选项中,选出符合题目的一项)
- 在中,如果,,那么等于( )
A. B. C. D.
- 自新冠肺炎疫情发生以来,全国人民共同抗疫,各地积极普及科学防控知识,下面是科学防控知识的图片,图片上有图案和文字说明,其中图案是轴对称图形的是( )
A. 打喷嚏 捂口鼻 B. 喷嚏后 慎揉眼
C. 勤洗手 勤通风 D. 戴口罩 讲卫生
- 下列事件中,随机事件是( )
A. 购买一张福利彩票中奖了
B. 通常水加热到时会沸腾
C. 在地球上,抛出的篮球会下落
D. 掷一枚骰子,向上一面的字数一定大于零
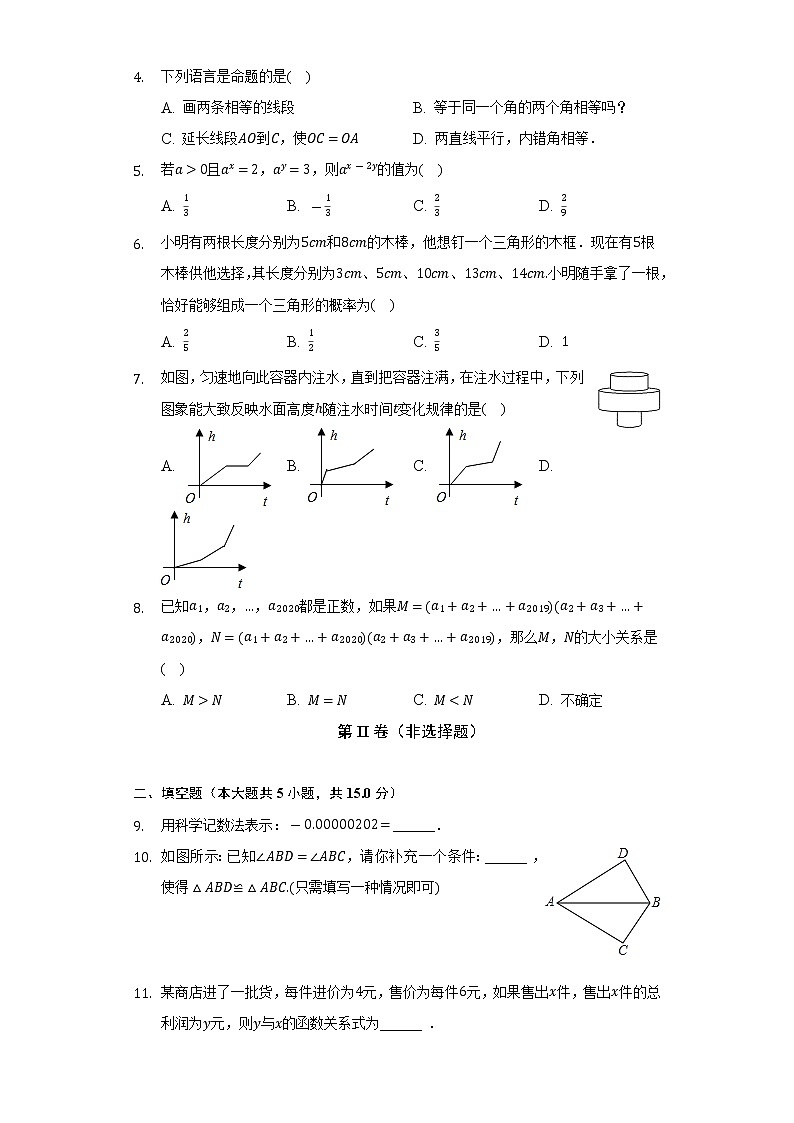
- 下列语言是命题的是( )
A. 画两条相等的线段 B. 等于同一个角的两个角相等吗?
C. 延长线段到,使 D. 两直线平行,内错角相等.
- 若且,,则的值为( )
A. B. C. D.
- 小明有两根长度分别为和的木棒,他想钉一个三角形的木框.现在有根木棒供他选择,其长度分别为、、、、小明随手拿了一根,恰好能够组成一个三角形的概率为( )
A. B. C. D.
- 如图,匀速地向此容器内注水,直到把容器注满,在注水过程中,下列图象能大致反映水面高度随注水时间变化规律的是( )
A. B. C. D.
- 已知,,,都是正数,如果,,那么,的大小关系是( )
A. B. C. D. 不确定
第II卷(非选择题)
二、填空题(本大题共5小题,共15.0分)
- 用科学记数法表示:______.
- 如图所示:已知,请你补充一个条件:______ ,使得≌只需填写一种情况即可
- 某商店进了一批货,每件进价为元,售价为每件元,如果售出件,售出件的总利润为元,则与的函数关系式为______ .
- 如图,中,垂直平分,若的周长为,,则 ______ .
- 如图,长方体的底面边长分别为 和,高为如果用一根细线从点开始经过个侧面缠绕一圈到达点,那么所用细线最短需要______.
三、解答题(本大题共11小题,共81.0分。解答应写出文字说明,证明过程或演算步骤)
- 计算:
;
. - 化简求值:,其中.
- 如图,用尺规在的右侧作不写作法,只需保留作图痕迹.
- 如图,直线,点在直线上,且,,求的度数.
- 全校举办了文艺汇演活动.小丽和小芳都想当节目主持人,但现在只有一个名额.小丽想出了一个办法,她将一个转盘质地均匀平均分成份,如图所示.游戏规定:随意转动转盘,若指针指到,则小丽去;若指针指到,则小芳去这个游戏规定对双方公平吗?为什么?若不公平,请修改游戏规定,使这个游戏对双方公平.
- 一个零件的形状如图所示,按规定,和分别是和的零件为合格零件,现质检工人量得,就断定这个零件不合格,请你运用三角形的有关知识说明零件不合格的理由.
- 完成下面的证明过程
已知:如图,,于,于,.
求证:≌.
证明:,______两直线平行,内错角相等
,,
______.
,______.
在和中,
≌______.
- 已知:点、、、在同一条直线上,,,求证:.
- 受疫情的影响,各类学校纷纷延迟开学时间,教育部提倡“停课不停教,停课不停学”的在线教学方式.寒假期间,线上教育的用户使用量猛增,现“钉钉”平台整理出“线上教学”项目投入资金及预计利润如表:
投入资金亿元 | |||||||
预计利润千万元 |
如表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
如果预计获得千万元的利润,投入资金应为______亿元.
如果公司可以拿出亿元进行“线上教学”项目的投资,预计利润是多少?说说理由.
- 阅读下面的材料,然后解答问题:
我们新定义一种三角形,两边的平方和等于第三边平方的倍的三角形叫做奇异三角形.
理解并填空:
根据奇异三角形的定义,请你判断:等边三角形一定是奇异三角形吗?______填“是”或“不是”
若某三角形的三边长分别为、、,则该三角形______填“是”或“不是”奇异三角形.
探究:在,两边长分别是、,且,,则这个三角形是否是奇异三角形?请说明理由. - 如图,点、在直线上,点、在直线上,平分,平分且
判断直线与的位置关系,并说明理由;
如图,为线段上一定点,为直线上一动点,当点在直线上运动时不与点合,猜想、与之间的数量关系,并说明理由.
答案和解析
1.【答案】
【解析】解:,
,
故选:.
根据三角形内角和为求解即可.
本题考查三角形内角和定理,解题的关键是熟练掌握基本知识,属于中考基础题.
2.【答案】
【解析】解:、不是轴对称图形,不合题意;
B、不是轴对称图形,不合题意;
C、不是轴对称图形,不合题意;
D、是轴对称图形,符合题意.
故选D.
根据轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形进行分析即可.
此题主要考查了轴对称图形,正确掌握轴对称图形的性质是解题关键.
3.【答案】
【解析】解:
A、购买一张福利彩票中奖了是随机事件,故本选项正确;
B、通常水加热到时会沸腾是必然事件,故本选项错误;
C、在地球上,抛出的篮球会下落是必然事件,故本选项错误;
D、掷一枚骰子,向上一面的字数一定大于零是必然事件,故本选项错误;
故选A.
根据随机事件和必然事件的定义对各选项进行逐一分析即可得出答案.
本题考查的是随机事件,事件分为确定事件和不确定事件随机事件,确定事件又分为必然事件和不可能事件,其中,必然事件发生的概率为,即必然事件;不可能事件发生的概率为,即不可能事件;如果为不确定事件随机事件,那么.
4.【答案】
【解析】解:根据命题的定义:
只有答案D、两直线平行,内错角相等.对事情做出正确或不正确的判断,故此选项正确;
故选:.
根据命题的定义解答,命题是对事情做出正确或不正确的判断的句子叫做命题,分别判断得出答案即可.
本题考查了命题的定义,利用定义得出是解题关键.
5.【答案】
【解析】解:.
故选:.
逆用同底数幂的除法法则进行变形,然后再逆用幂的乘方法则变形最后将,代入计算即可.
本题主要考查的是同底数幂的除法法则的应用,熟练掌握相关法则是解题的关键.
6.【答案】
【解析】解:小明随手拿了一根,有五种情况,由于三角形中任意两边之和要大于第三边,任意两边之差小于第三边,故只有这根是或,
小明随手拿了一根,恰好能够组成一个三角形的概率.
故选:.
根据构成三角形的条件,确定出第三边长,再由概率求解.
用到的知识点为:概率所求情况数与总情况数之比;三角形两边之和大于第三边.
7.【答案】
【解析】解:最下面的容器容器最小,用时最短,第二个容器最粗,那么第二个阶段的函数图象水面高度随时间的增大而增长缓慢,用时较长,最上面容器较粗,那么用时较短.
故选:.
由于三个容器的高度相同,粗细不同,那么水面高度随时间变化而分三个阶段.
此题主要考查了函数图象,解决本题的关键是根据容器的高度相同,每部分的粗细不同得到用时的不同.
8.【答案】
【解析】
【分析】
本题主要考查了整式的混合运算,熟练掌握运算法则是解题的关键.另外,像本题中将一个整式设为一个字母这种方法在很多题型中也很常见,也需重点掌握.
设,用分别表示出,,再利用作差法比较大小即可.
【解答】
解:设,则
都是正数
故选:.
9.【答案】
【解析】解:.
故答案为:.
绝对值小于的正数也可以利用科学记数法表示,一般形式为,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的的个数所决定.
本题考查了科学记数法.解题的关键是掌握用科学记数法表示较小的数,一般形式为,其中,为由原数左边起第一个不为零的数字前面的的个数所决定.
10.【答案】或或
【解析】解:和中,已知;
当或或时,≌.
故答案为:或或.
要使得≌,已知、,则可以添加边,运用来判定其全等,也可添加一组角运用来判定其全等.
本题考查三角形全等的判定方法;判定两个三角形全等的一般方法有:、、、、添加时注意:、不能判定两个三角形全等,不能添加,根据已知结合图形及判定方法选择条件是正确解答本题的关健.
11.【答案】
【解析】解:根据题意可得:
每件进价为元,售价为每件元,
每件商品的利润为:元,
与的函数关系式为:.
故答案为:.
首先求出每件商品的利润,进而得出与的函数关系式.
此题主要考查了函数关系式,正确利用每件利润销量总利润得出函数关系式是解题关键.
12.【答案】
【解析】解:垂直平分,
,
的周长为,
,
即,
,又,
,
故答案为:.
根据线段的垂直平分线的性质得到,根据已知和三角形的周长公式计算即可.
本题考查的是线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
13.【答案】
【解析】解:将长方体展开,连接、,
,,
根据两点之间线段最短,.
故答案为:.
要求所用细线的最短距离,需将长方体的侧面展开,进而根据“两点之间线段最短”得出结果.
考查了平面展开最短路径问题,本题就是把长方体的侧面展开“化立体为平面”,用勾股定理解决.
14.【答案】解:
;
.
【解析】先算乘方,再算乘法,后算加减,即可解答;
先化简各式,然后再进行计算即可解答.
本题考查了同底数幂的乘法,零指数幂,负整数指数幂,有理数的加减混合运算,绝对值,幂的乘方与积的乘方法则,熟练掌握它们的运算法则是解题的关键.
15.【答案】解:原式
,
,
且,
解得:,,
则原式.
【解析】原式中括号里利用平方差公式,以及完全平方公式化简,去括号合并后利用多项式除以单项式法则计算,去括号合并得到最简结果,利用非负数的性质求出与的值.代入计算即可求出值.
此题考查了整式的混合运算化简求值,以及非负数的性质,熟练掌握运算法则是解本题的关键.
16.【答案】解:如图,为所作.
【解析】利用基本作图,作一个角等于已知角画出.
本题考查了作图基本作图:熟练掌握种基本作图是解决问题的关键.
17.【答案】解:如图:,
,
又,
,
,
,
.
【解析】根据两条直线平行,同位角相等,得的同位角的度数.再根据平角的定义即可求得.
本题考查了平行线的性质,平角的概念,熟记平行线的性质是解题的关键.
18.【答案】解:不公平,
小丽获胜的概率为、小芳获胜的概率为,
,
此游戏不公平;
修改规则为:若指针转到偶数,则小丽胜;若指正转到奇数,则小芳胜.
【解析】分别计算出转出的数是的概率和是的概率即可得到游戏是否公平.
本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.用到的知识点为:概率所求情况数与总情况数之比.
19.【答案】解:如图,延长交于,
,,
,
,
.
又,
这个零件不合格.
【解析】延长交于,根据三角形的一个外角等于与它不相邻的两个内角的和列式求出,然后即可判断.
本题考查的是三角形外角的性质,根据题意作出辅助线,构造出三角形,利用三角形外角的性质求解是解答此题的关键.
20.【答案】
【解析】证明:,
两直线平行,内错角相等,
,,
,
,
,
在和中,
,
≌.
故答案为:;;;,,;.
根据,可得,根据于,于,可得,然后根据,可得,利用可证明≌.
本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:、、、、.
注意:、不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
21.【答案】证明:,
,
即:,
,
,
在和中,
≌,
,
.
【解析】首先利用证明≌,根据全等三角形对应角相等,可得,再根据“内错角相等,两直线平行”,即可证出.
此题主要考查了平行线的性质,全等三角形的判定,做题的关键是找出证三角形全等的条件.
22.【答案】
【解析】反映了投入资金和预计利润之间的关系,投入资金是自变量,预计利润是因变量;
从表格数据看,如果预计获得千万元的利润,投入资金应为亿元,
故答案为;
从表格数据看,与之间的关系为,
当时,,
故预计利润是千万元.
根据函数的定义即可求解;
查表格数据即可求解;
从表格数据看,与之间的关系为,进而求解.
本题考查了函数的表示方法,解决本题的关键是列出函数关系式.
23.【答案】解:是;
是;
当为斜边时,则,
则,,
不是奇异三角形;
当为斜边时,,
则有,
是奇异三角形,
答:当为斜边时,不是奇异三角形;当为斜边时,是奇异三角形.
【解析】
【分析】
本题考查的是勾股定理、奇异三角形的定义,如果直角三角形的两条直角边长分别是,,斜边长为,那么.
根据等边三角形的三边相等、奇异三角形的定义判断;
根据奇异三角形的定义判断;
分为斜边、为斜边两种情况,根据勾股定理、奇异三角形的定义判断.
【解答】
解:设等边三角形的边长为,则,
等边三角形一定是奇异三角形,
故答案为:是;
,,
,
该三角形是奇异三角形,
故答案为:是;
见答案.
24.【答案】解:,
理由如下:
如图中,
平分,平分已知,
,角平分线的定义,
又已知,
等量代换,
同旁内角互补,两直线平行.
如图中,当在点左侧时,过点作,
已证,
同平行于一条直线的两直线互相平行,
,两直线平行,内错角相等,
,两直线平行,同位角相等,
又,
等量代换.
如图中,当在点右侧时,过点作,
已证,
同平行于一条直线的两直线互相平行,
,,两直线平行,内错角相等,
又,
平角定义,
.
【解析】想办法证明即可;
分两种情形分别求解即可解决问题.
本题考查平行线的判定和性质、三角形内角和定理等知识,解题的关键是学会添加常用辅助线,构造平行线解决问题,属于中考常考题型.
陕西省渭南市华州区2021-2022学年七年级下学期期末考试数学试卷: 这是一份陕西省渭南市华州区2021-2022学年七年级下学期期末考试数学试卷,共11页。试卷主要包含了0分,0分),【答案】,【答案】或或等内容,欢迎下载使用。
陕西省渭南市华州区2021-2022学年八年级上学期期末考试数学试卷: 这是一份陕西省渭南市华州区2021-2022学年八年级上学期期末考试数学试卷,共8页。试卷主要包含了领到试卷和答题卡后,请用0,若一次函数等内容,欢迎下载使用。
陕西省渭南市华州区2021-2022学年九年级上学期期末考试数学试卷(含答案): 这是一份陕西省渭南市华州区2021-2022学年九年级上学期期末考试数学试卷(含答案),共9页。试卷主要包含了领到试卷和答题卡后,请用0等内容,欢迎下载使用。












