2020-2021学年4.2 直线、射线、线段多媒体教学课件ppt

4.2　直线、射线、线段

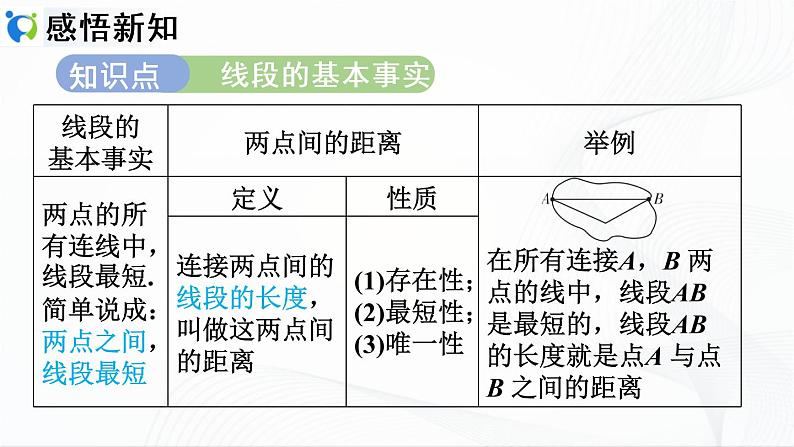
4.2.3　线段的基本事实及两点间的距离

【知识梳理】

(1)两点的所有连线中,　      　最短. 

简单说成:两点之间,　        　最短. 

(2)连接两点间的线段的　     　,叫做这两点的距离;两点间的距离是一个数,它不是图形. 

【基础强化】

知识点1　线段的性质

1.如图,铁路MN两旁各有两个工厂A,B.要在铁路上建一货站P,使它到两厂距离之和最短,则这个货站P应建在AB与MN的交点处,这种做法用几何知识解释应是(      )

A.两点之间的所有连线中,线段最短    B.射线只有一个端点

C.两直线相交只有一个交点           D.两点确定一条直线

2.如图，从点A到点B最短的路线是(　　)

A．A→G→E→B   B．A→C→E→B

C．A→D→G→E→B  D．A→F→E→B

3.西成高铁是中国首条穿越秦岭的高速铁路,大大减少了人们从西安到四川成都的时间,实现了人们“早上游大雁塔,晚上逛宽窄巷”的美好愿望.建造直隧道的目的可以用数学知识解释为　                      　. 

知识点2　两点的距离

4.A,B两点之间的距离是(      )

A.连接A,B两点的线段     B.连接A,B两点的直线

C.线段AB的长度          D.直线AB的长度

5.如图，AB＝12，C为AB的中点，点D在线段AC上，且AD∶CB＝1∶3，则D，B两点间的距离为(　　)

A．4 B．6 C．8 D．10

6.【2022南京师大附中月考】如图,直线上的四个点A,B,C,D分别代表四个小区,其中A小区和B小区相距a m(a<200),B小区和C小区相距200 m,C小区和D小区相距a m,某公司的员工在A小区有30人,B小区有5人,C小区有20人,D小区有6人,现公司计划在A,B,C,D四个小区中选一个作为班车停靠点,为使所有员工步行到停靠点的路程总和最小,那么停靠点的位置应设在(　　)

A.A小区         B.B小区 C.C小区       D.D小区

7.已知A,B,C都是直线l上的点,且AB＝7 cm,BC＝5 cm,那么点A与点C之间的距离为　    　. 

【知能提升】

一、选择题

1.下列说法中正确的是(　　)

A．两点之间直线最短

B．画出A，B两点间的距离

C．连接点A与B的线段，叫AB两点间的距离

D．两点之间的距离是一个数，不是指线段本身

2.如图所示，由M到N有①②③④共4条路线，最短的路线选①的理由是(　　)

A．因为它是直线

B．两点确定一条直线

C．两点之间的距离

D．两点之间，线段最短

3.下列生活、生产现象中,不能用“两点之间,线段最短”来解释的现象有(      )

①用两颗钉子就可以把木条固定在墙上;

②植树时,只要栽下两棵树,就可以把同一行树栽在同一条直线上;

③从A到B架设电线,总是尽可能沿线段AB架设;

④把弯曲的公路改直,就能缩短路程.

A.①② B.①③ C.②④ D.③④

4.已知线段AB＝8 cm，点P到A，B两点的距离相等，则PA＋PB的长为(　　)

A．等于8 cm B．小于8 cm

C．不小于8 cm D．大于8 cm

二、填空题

5.如图,已知空间站A与星球B距离为a,信号飞船C在星球B附近沿圆形轨道行驶,B,C之间的距离为b.数据S表示飞船C与空间站A的实时距离,那么S的最大值是　　. 

三、解答题

6.如图,平面上有A,B,C,D四个村庄,为解决当地缺水问题,政府准备修建一个蓄水池,不考虑其他因素,请你画出蓄水池P的位置,使它与四个村庄的距离之和最小.

7.如图，一只壁虎要从圆柱体A点沿着表面爬到B点，因为B点处有它想吃的一只蚊子，而它饿得快不行了，怎样爬行路线最短？

8.知识是用来为人类服务的,我们应该把它们用于有意义的方面.请你对下面两个情景做出评判.

情景1:从教室到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢?试用所学数学知识来说明这个问题.

情景2:A,B是河流l两旁的两个村庄,现要在河边修一个抽水站向两村供水,问抽水站修在什么地方才能使所需的管道最短?请在图中表示出抽水站点P的位置,并说明你的理由.

你赞同以上哪种做法?你认为应用数学知识为人类服务时应注意什么?

9.【2022北京西城区期中】如图,已知数轴上三点M,O,N对应的数分别为-1,0,3,点P为数轴上任意一点,其对应的数为x.

(1)MN的长为　　　　. 

(2)当点P到点M、点N的距离相等时,求x的值.

(3)数轴上是否存在点P,使点P到点M、点N的距离之和是8?若存在,求出x的值;若不存在,请说明理由.

(4)如果点P以每秒1个单位长度的速度从点O沿数轴向左运动,同时点A和点B分别从点M和点N出发以每秒2个单位长度和每秒3个单位长度的速度也沿数轴向左运动.当点P到点A、点B的距离相等时,直接写出t的值.

参考答案

【知识梳理】

(1)两点的所有连线中,　   线段     　最短. 

简单说成:两点之间,　   线段     　最短. 

(2)连接两点间的线段的　  长度   　,叫做这两点的距离;两点间的距离是一个数,它不是图形. 

【基础强化】

知识点1　线段的性质

1.如图,铁路MN两旁各有两个工厂A,B.要在铁路上建一货站P,使它到两厂距离之和最短,则这个货站P应建在AB与MN的交点处,这种做法用几何知识解释应是(   A   )

A.两点之间的所有连线中,线段最短    B.射线只有一个端点

C.两直线相交只有一个交点           D.两点确定一条直线

2.如图，从点A到点B最短的路线是(　D　)

A．A→G→E→B   B．A→C→E→B

C．A→D→G→E→B  D．A→F→E→B

3.西成高铁是中国首条穿越秦岭的高速铁路,大大减少了人们从西安到四川成都的时间,实现了人们“早上游大雁塔,晚上逛宽窄巷”的美好愿望.建造直隧道的目的可以用数学知识解释为　两点之间的所有连线中,线段最短　. 

知识点2　两点的距离

4.A,B两点之间的距离是(   C   )

A.连接A,B两点的线段     B.连接A,B两点的直线

C.线段AB的长度          D.直线AB的长度

5.如图，AB＝12，C为AB的中点，点D在线段AC上，且AD∶CB＝1∶3，则D，B两点间的距离为(　D　)

A．4 B．6 C．8 D．10

6.【2022南京师大附中月考】如图,直线上的四个点A,B,C,D分别代表四个小区,其中A小区和B小区相距a m(a<200),B小区和C小区相距200 m,C小区和D小区相距a m,某公司的员工在A小区有30人,B小区有5人,C小区有20人,D小区有6人,现公司计划在A,B,C,D四个小区中选一个作为班车停靠点,为使所有员工步行到停靠点的路程总和最小,那么停靠点的位置应设在(　B　)

A.A小区         B.B小区 C.C小区       D.D小区

【解析】当停靠点在A小区时,所有员工步行到停靠点路程和是5a+20×(200+a)+6(2a+200)=(37a+5 200)(m).当停靠点在B小区时,所有员工步行到停靠点路程和是30a+20×200+6(a+200)=(36a+5 200)(m).当停靠点在C小区时,所有员工步行到停靠点路程和是30(a+200)+5×200+6a=(36a+7 000)(m).当停靠点在D小区时,所有员工步行到停靠点路程和是30×(2a+200)+5(a+200)+20a=(85a+7 000)(m).因为36a+5 200<37a+5 200<36a+7 000<85a+7 000,所以当停靠点在B小区时,所有员工步行到停靠点路程和最小,所以停靠点的位置应该在B小区.

7.已知A,B,C都是直线l上的点,且AB＝7 cm,BC＝5 cm,那么点A与点C之间的距离为　12 cm或2 cm　. 

【知能提升】

一、选择题

1.下列说法中正确的是(　D　)

A．两点之间直线最短

B．画出A，B两点间的距离

C．连接点A与B的线段，叫AB两点间的距离

D．两点之间的距离是一个数，不是指线段本身

2.如图所示，由M到N有①②③④共4条路线，最短的路线选①的理由是(　D　)

A．因为它是直线

B．两点确定一条直线

C．两点之间的距离

D．两点之间，线段最短

3.下列生活、生产现象中,不能用“两点之间,线段最短”来解释的现象有(   A   )

①用两颗钉子就可以把木条固定在墙上;

②植树时,只要栽下两棵树,就可以把同一行树栽在同一条直线上;

③从A到B架设电线,总是尽可能沿线段AB架设;

④把弯曲的公路改直,就能缩短路程.

A.①② B.①③ C.②④ D.③④

4.已知线段AB＝8 cm，点P到A，B两点的距离相等，则PA＋PB的长为(　C　)

A．等于8 cm B．小于8 cm

C．不小于8 cm D．大于8 cm

二、填空题

5.如图,已知空间站A与星球B距离为a,信号飞船C在星球B附近沿圆形轨道行驶,B,C之间的距离为b.数据S表示飞船C与空间站A的实时距离,那么S的最大值是　a＋b　. 

三、解答题

6.如图,平面上有A,B,C,D四个村庄,为解决当地缺水问题,政府准备修建一个蓄水池,不考虑其他因素,请你画出蓄水池P的位置,使它与四个村庄的距离之和最小.

解:连接AC,BD,交点P即为所求位置.

7.如图，一只壁虎要从圆柱体A点沿着表面爬到B点，因为B点处有它想吃的一只蚊子，而它饿得快不行了，怎样爬行路线最短？

解：将圆柱体的侧面展开，如答图所示，连接AB，则线段AB是壁虎爬行的最短路线．

8.知识是用来为人类服务的,我们应该把它们用于有意义的方面.请你对下面两个情景做出评判.

情景1:从教室到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢?试用所学数学知识来说明这个问题.

情景2:A,B是河流l两旁的两个村庄,现要在河边修一个抽水站向两村供水,问抽水站修在什么地方才能使所需的管道最短?请在图中表示出抽水站点P的位置,并说明你的理由.

你赞同以上哪种做法?你认为应用数学知识为人类服务时应注意什么?

解:情景1:因为两点之间的所有连线中,线段最短.

情景2:连接AB,交直线l于点P,点P即为抽水站的位置.图略.

理由:两点之间的所有连线中,线段最短.

赞同情景2中的做法.应用数学知识为人类服务时应注意不能以破坏环境为代价.

9.【2022北京西城区期中】如图,已知数轴上三点M,O,N对应的数分别为-1,0,3,点P为数轴上任意一点,其对应的数为x.

(1)MN的长为　　　　. 

(2)当点P到点M、点N的距离相等时,求x的值.

(3)数轴上是否存在点P,使点P到点M、点N的距离之和是8?若存在,求出x的值;若不存在,请说明理由.

(4)如果点P以每秒1个单位长度的速度从点O沿数轴向左运动,同时点A和点B分别从点M和点N出发以每秒2个单位长度和每秒3个单位长度的速度也沿数轴向左运动.当点P到点A、点B的距离相等时,直接写出t的值.

解:(1)4

MN的长为3-(-1)=4.

(2)根据题意,得x-(-1)=3-x,解得x=1.

(3)①当点P在点M的左侧时.

根据题意,得-1-x+3-x=8,解得x=-3.

②当点P在点M和点N之间时,

则x-(-1)+3-x=8,方程无解,

即点P不可能在点M和点N之间.

③当点P在点N的右侧时,

根据题意,得x-(-1)+x-3=8,解得x=5.

所以x的值是-3或5.

(4)t的值为或4.

设运动t秒时,点P到点A,点B的距离相等,即PA=PB.

根据题意,得点P对应的数是-t,点A对应的数是-1-2t,点B对应的数是3-3t.

①当点A和点B在点P同侧时,点A和点B重合,

所以-1-2t=3-3t,解得t=4,符合题意.

②当点A和点B在点P异侧时,点A位于点P的左侧,点B位于点P的右侧(因为三个点都向左运动,出发时点A在点P左侧,且点A运动的速度大于点P的速度,所以点A永远位于点P的左侧),

则PA=-t-(-1-2t)=t+1,PB=(3-3t)-(-t)=3-2t.

所以t+1=3-2t,解得t=,符合题意.

综上所述,t的值为或4.