初中数学北师大版九年级上册第二章 一元二次方程6 应用一元二次方程背景图ppt课件

这是一份初中数学北师大版九年级上册第二章 一元二次方程6 应用一元二次方程背景图ppt课件，文件包含262《一元二次方程的应用营销问题》课件PPTpptx、262《一元二次方程的应用营销问题》教案docx等2份课件配套教学资源，其中PPT共17页， 欢迎下载使用。
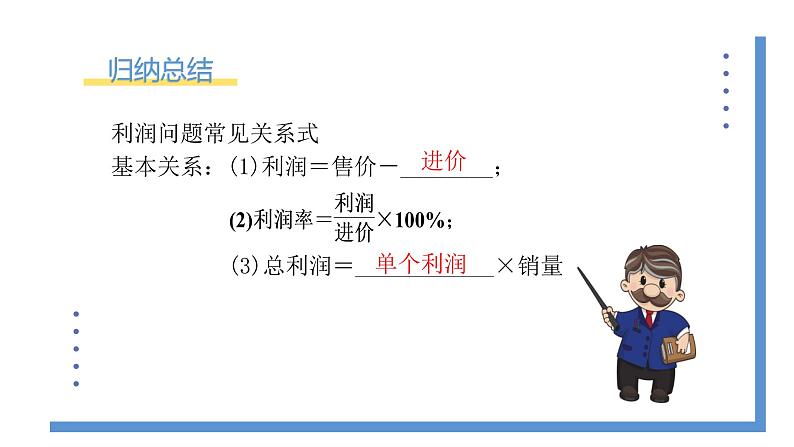
北师大版数学九年级上册《2.6.2一元二次方程的应用——营销问题》教学设计课题名2.6.2一元二次方程的应用——营销问题教学目标1.经历分析具体问题中的数量关系、建立方程模型并解决问题的过程，进一步体会方程是刻画现实世界中数量关系的一个有效的数学模型．2．总结运用方程解决实际问题的一般步骤，进一步提高分析问题、解决问题的能力.3.会建立一元二次方程模型，解决生活实际中的问题，能根据具体问题的实际意义检验结果的合理性.教学重点能够利用一元二次方程解决有关实际问题，并能根据具体问题的实际意义检验结果的合理性.教学难点能根据具体问题中的数量关系建立方程模型并解决问题.教学准备教师准备：熟悉课本和课件.学生准备：复习营销问题的数量关系和增长或降低的有关知识.教学过程一、复习问题1：小明学习非常认真，学习成绩直线上升，第一次月考数学成绩是75分，第二次月考增长了20%，第三次月考又增长了20%，问他第三次数学成绩是多少？第二次数学成绩：75×(1+20%)=90第三次数学成绩：90×(1+20%)=108或第三次数学成绩：5×(1+20%)2=108二、例题讲解例2   新华商场销售某种冰箱，每台进货价为2 500元.调查发现，当销售价为2 900元时，平均每天能售出8台；而当销售价每降低50元时，平均每天就能多售出4台.商场要想使这种冰箱的销售利润平均每天达到5 000元，每台冰箱的定价应为多少元？ 分析：本题的主要等量关系：每台冰箱的销售利润×平均每天销售冰箱的数量=5 000元如果设每台冰箱降价x元，那么每台冰箱的定价就是                 元，每台冰箱的销售利润为                              ____________________元，平均每天销售冰箱的数量为                台.解：设每台冰箱降价x元，由题意得：   解方程，得x1=x2=150.经检验x1=x2=150符合题意，是原方程的解.定价为2 900-150=2 750（元）.答：每台冰箱的定价应为2 750元.合作交流做一做：某商场将进货价为30元的台灯按40元出售，平均每月能卖600个，调查发现，售价在40元至60元范围内，这种台灯的售价每上涨1元，其销售量就要减少10个，为了实现平均每月10000元的销售利润，这种台灯的售价应定为多少？这时应购进台灯多少个？分析：设商品售价为x元，则每个商品得利润________元，因为每涨价1元，其销售会减少10个，其销售量会减少_____________个，故销售量为__________________个，根据每件商品的利润×销售量=10000，则______________________________________.解：设商品售价为x元，则销售价为(40+x)元，销售量为(600-10x)个，则[600－10（x-40）]· (x-30)=10000，整理得 x2－130x+4000=0，                             解得x1=50，x2=80（舍去）.当x=50时，600-10（x-40）=600-10（50-40）=500（个）；答：要想赚10000元，售价定为50元；这时进货量应为500个. 利润问题常见关系式基本关系：(1)利润＝售价－进价；         （2）利润率=(3)总利润＝单个利润×销量例3：为做好延迟开学期间学生的在线学习服务工作，某市教育局推出“中小学延迟开学期间网络课堂”，为学生提供线上学习，据统计，第一批公益课受益学生20万人次，第三批公益课受益学生24.2万人次．如果第二批，第三批公益课受益学生人次的增长率相同，求这个增长率.解：设增长率为x，根据题意，得20（1+x）2=24.2.解得x1=-2.1（舍去），x2=0.1=10%．答：增长率为10%.例4：前年生产1吨甲种药品的成本是5000元，随着生产技术的进步，现在生产1吨甲种药品的成本是3000元，试求甲种药品成本的年平均下降率是多少？解：设甲种药品的年平均下降率为x.根据题意，列方程，得5 000 ( 1－x )2 = 3000，解方程，得x1≈0.225，x2≈1.775.根据问题的实际意义，甲种药品成本的年平均下降率约为22.5％.三、归纳总结类似地 这种增长率的问题在实际生活中普遍存在,有一定的模式.若平均增长(或降低)百分率为x,增长(或降低)前的是a,增长(或降低)n次后的量是b,则它们的数量关系可表示为a(1±x)n=b(其中增长取“+”,降低取“－”).四、过关练习1.光彩市场其个体商户购进某种电子产品的进价是50元/个，根据市场调研发现售价是80元/个时，每周可卖出160个，若销售单价每降低2元，则每周可多卖出20个．若商户计划下周利润达到5 200元，则此电子产品的售价为每个多少元？设销售价格每个降低x元(x为偶数)，则所列方程为(　　)A．(80－x)(160＋20x)＝5 200   B．(30－x)(160＋20x)＝5 200C．(30－x)(160＋10x)＝5 200   D．(50－x)(160＋10x)＝5 200答案C2.（2022泰安中考）我国古代著作《四元玉鉴》记载“买椽多少”问题：“六贯二百一十钱，遣人去买几株椽．每株脚钱三文足，无钱准与一株椽．”其大意为：现请人代买一批椽，这批椽的价钱为6210文．如果每株椽的运费是3文，那么少拿一株椽后，剩下的椽的运费恰好等于一株椽的价钱，试问6210文能买多少株椽？设这批椽的数量为x株，则符合题意的方程是（　　）A．3(x-1)x＝6210   B．3(x-1)＝6210C．(x-1)x＝6210    D．3x=6210答案A3.（2022重庆中考）小区新增了一家快递店，第一天揽件200件，第三天揽件242件，设该快递店揽件日平均增长率为x，根据题意，下面所列方程正确的是（　　）A．200(1+x)2＝242  B．200(1-x)2＝242 C．200(1+2x)＝242    D．200(1-2x)＝242 答案A4. 某新华书店计划第一季度共发行图书122万册，其中一月份发行图书32万册，二、三月份平均每月的增长率相同.求二、三月份各应发行图书多少万册？解：设平均每月的增长率为x.    依题意，32+32(1+x)+32(1+x)2=122.    解得x1=0.25，x2=-3.25(舍去).    二月份发行图书32×(1+0.25)=40(万册)    三月份发行图书32×(1+0.25)2=50(万册)答：二月份发行图书40万册，三月份发行图书50万册. 5.百佳超市将进货单价为40元的商品按50元出售时，能卖500个，已知该商品要涨价1元，其销售量就要减少10个，为了赚8000元利润，售价应定为多少，这时应进货为多少个？解：设每个商品涨价x元，则销售价为(50+x)元，销售量为(500－10x)个，则(500－10x)· [(50+x)－40]=8000，整理得 x2－40x+300=0，                             解得x1=10，x2=30都符合题意.当x=10时，50+x =60，500－10 x=400；当x=30时，50+x =80， 500－10 x=200.答：要想赚8000元，售价为60元或80元；若售价为60元，则进货量应为400；若售价为80元，则进货量应为200个.五、课堂总结营销问题：常用公式：总利润=单件利润×销量=（售价-进价）×销量平均变化率问题：①增长率问题：a(1+x)2=b，其中a为增长前的量，x为增长率，2为增长次数，b为增长后的量.②降低率问题：a(1-x)2=b，其中a为降低前的量，x为降低率，2为降低次数，b为降低后的量.注意1与x位置不可调换. 布置作业 教材第55页习题2.10第2、3题. 板书设计课题：2.6.2 应用一元二次方程——营销问题一、解决销售问题二、平均变化率问题 教学反思设未知数(未知量成了已知量)，带着未知量去“翻译 ”题目申的有关信息，然后将这些含有的量表示成等量关系，就是应用题的解题策略。无论是例题的分析还是练习的分析，尽可能地鼓励学生动脑、动手、动口，为学生提供展示自己聪明才智的机会，并且在此过程中更利于教师发现学生分析问题解决问题的独到见解以及思维的误区，以便指导今后的教学。课堂上要把激发学生学习热情和获得学习能力放在首位，通过运用各种启发、激励的语言，以及组织小组合作学习，帮助学生形成积极主动的求知态度。