







- 1.3.1《空间直角坐标系》课件+教案 课件 76 次下载
- 1.3.2《空间向量运算的坐标表示》课件+教案 课件 78 次下载
- 1.4.1(2)《空间中直线、平面的平行》课件+教案 课件 75 次下载
- 1.4.1(3)《空间中直线、平面的垂直》课件+教案 课件 74 次下载
- 1.4.2(1)《用空间向量研究距离问题》课件+教案 课件 77 次下载
高中数学人教A版 (2019)选择性必修 第一册第一章 空间向量与立体几何1.4 空间向量的应用教学课件ppt
展开人教A版2019高中数学选修一
《空间在点、直线和平面的向量表示》教学设计
课题 | 空间中点、直线和平面的向量表示 |
教学目标 | 1.利用空间向量基本定理得到空间中点、直线、平面的向量表示,提升直观想象和逻辑推理的素养. 2.会求平面的方向向量、法向量,提升数学运算的素养. |
教学重点 | 空间中点、直线和平面的向量表示及其平面法向量的求法。 |
教学难点 | 利用对比的手法寻找空间中点、直线和平面的向量表示方法,求平面的法向量。 |
教学准备 | 教师准备:正方体、长方体、等教具,PPT课件. 学生准备:相应的教学模型。阅读课本P26—P29 |
教学过程 | 一、导入新课:
空间向量可以解决哪些立体几何问题呢?
老师通过PPT向学生展示认识知识的阶梯过渡及转化与化归思想的再认识,同时提出如何用向量法表示空间中的有关元素及怎样解决由这些元素构成的几何体的相关问题?提出问题,引起悬念,从而导出新课,进一步启发学生用对比的手法学习这节课的内容。 二、知识梳理: 通过上面的图示,提出问题,引起悬念,进一步带领学生探究空间中点、直线和平面的向量表示以及应用。阅读课本P26-P29,回答下列问题: 1.对比探讨: (1)问题起因: 点、线、面是空间的基本图形,点、线段、平面图形是组成空间几何体的基本元素.因此,为了用空间向量研究立体几何问题,首先要用向量表示空间中的点、线、面. (2)思考下列问题: ①如何用向量表示空间中的一个点? 答:坐标(x,y,z) 如图所示,在空间中,取一定点O作为基点,那么空间中任意一点可以用来表示,我们把称为点的位置向量
②如何用向量表示空间中的直线? 答:点、方向向量. 如图所示,向量是直线的方向向量,在直线上取设是直线上 的任意一点,由向量共线可知:点在直线上存在实数,使得,即=
进一步地,如图,取定空间中的任意一点O,可以得到:在直线上的充要条件是:存在实数t,使 =+t ① 或=+t ② ① 、②式称为空间直线的向量表示式. 由此可知,空间任意直线由直线上一点及直线的方向向量唯一确定. =
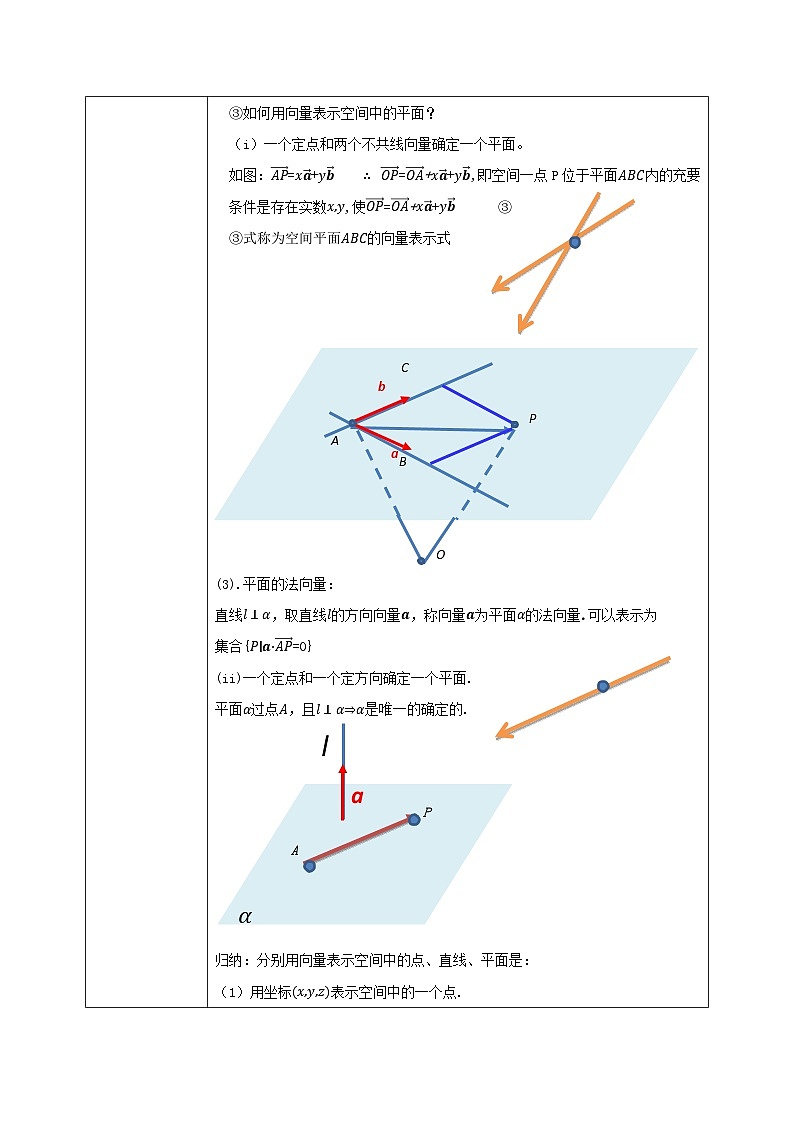
③如何用向量表示空间中的平面? (i)一个定点和两个不共线向量确定一个平面。 如图:=+ =++,即空间一点P位于平面内的充要条件是存在实数,使=++ ③ ③式称为空间平面的向量表示式
(3).平面的法向量: 直线,取直线的方向向量,称向量为平面的法向量.可以表示为 集合{=0} (ii)一个定点和一个定方向确定一个平面. 平面过点,且是唯一的确定的.
归纳:分别用向量表示空间中的点、直线、平面是: (1)用坐标表示空间中的一个点. (2)用点、方向向量表示空间中的一条直线. (3)用向量表示空间中的平面有两种方法: (i)一个定点和两个不共线向量确定一个平面; (ii)一个定点和一个定方向确定一个平面.
学以致用是每个人必备的思维模型,特别是学生,更要会化解知识体系,故请看下面的练习。 三、跟踪练习: 概念辨析: 1.判断下列命题是否正确: (1)零向量不能作为直线的方向向量和平面的法向量。( ) (2)若向量v是直线的方向向量,则也是直线的方向向量。 ( ) (3)在空间直角坐标系中是坐标平面的一个法向量。 答案:(1)√ (2)× (3)√
拓展和提升本节课的数学知识和思维方法是数学学习中必不可少的一个重要环节,请学习下一个环节。 四、课堂互动: 互动一: 1.在长方体中,,,以为原点,以 {, , }为空间的一个单位正交基底,建立空间直角坐标系求平面的一个法向量.
解:由已知,得
设平面的法向量为 则 即 令,则, 是平面的一个法向量. 互动二: 2.已知长方体A1B1C1D1中,,CC1为中点.以为原点,DD1所在直线分别为轴、轴、轴建立如图所示空间直角坐标系,(1)求平面的一个法向量.(2)求平面的一个法向量
解:(1)轴垂直于平面C1B1 )是C1B1的一个法向量. (2) CC1是的中点
设是平面A1的法向量,则 即 令,则, 是平面MCA1的一个法向量 数学核心素养价值观的形成是当今数学课改中必不可少的,请回答下列问题 五、素养形成 1.(多选题)如图,正方体中,其棱长为1,则下列结论正确的是( ) A.直线的一个方向向量为. B.直线的一个方向向量为. C.平面一个法向量为 D.平面一个法向量为 答案:A、B、C.
及时总结,归纳概括,是学习中必须学会的思维模式,进一步提升和拓展,请看: 六、课堂总结: 1.知识清单:(1)空间中点、直线和平面的向量表示: (i) 点→点+位置向量; (ii) 线→点+方向向量 (iii)平面→点+法向量或点+不共线的两个向量. (2)平面法向量的求法. 2.解题技巧:结合图形 ,巧妙建立空间直角坐标系,充分利用空间中点、直线、平面的向量表示求直线的方向向量、平面的法向量. |
课后作业 | 课本P29: 练习:1、2、3. 课本P41: 习题 1.4 1、2. |
板书设计 | 1.空间中点用向量如何表示? 课堂互动:1. 2.空间中直线用向量如何表示? 2. 3.空间中平面用向量如何表示? 素养训练:1. 跟踪练习:1. |
教学反思 | 1.对比手法在学习数学中经常出现,故应该充分体会它的优点并能灵活的应用之解决有关的数学问题。 2.数形结合思想的充分体现和提升,值得加强训练。 3.充分体会和认识数学思想及空间想象能力的拓展. |
数学人教A版 (2019)1.4 空间向量的应用课文内容ppt课件: 这是一份数学人教A版 (2019)1.4 空间向量的应用课文内容ppt课件,共16页。
高中数学人教A版 (2019)选择性必修 第一册1.4 空间向量的应用评课ppt课件: 这是一份高中数学人教A版 (2019)选择性必修 第一册1.4 空间向量的应用评课ppt课件,共54页。
人教A版 (2019)选择性必修 第一册1.4 空间向量的应用精品ppt课件: 这是一份人教A版 (2019)选择性必修 第一册1.4 空间向量的应用精品ppt课件,共49页。PPT课件主要包含了2-1-3,学习探究,求平面法向量,如何求平面法向量,激趣诱思,知识点拨,答案-1215,探究一,探究二,探究三等内容,欢迎下载使用。














