






高考数学二轮复习第2部分专题篇素养提升专题2数列第2讲数列求和及其综合应用课件
展开第2讲 数列求和及其综合应用(文理)
1 解题策略 · 明方向
2 考点分类 · 析重点
3 易错清零 · 免失误
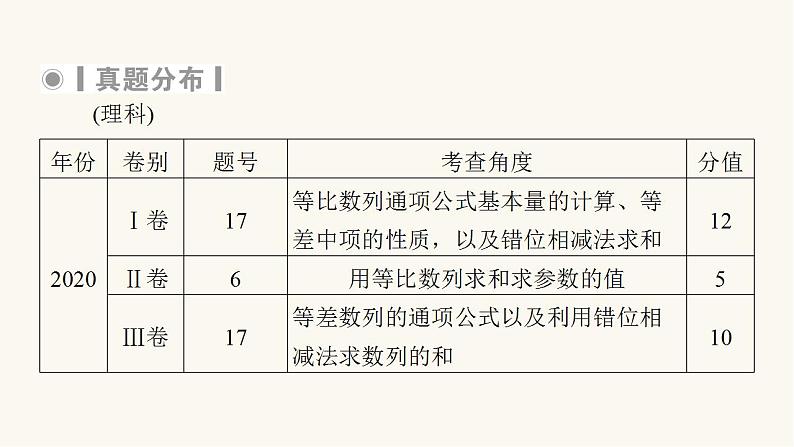
4 真题回放 · 悟高考
5 预测演练 · 巧押题
01 解题策略 · 明方向
1.高考对数列求和的考查主要以解答题的形式出现,通过分组转化、错位相减、裂项相消等方法求数列的前n项和,难度中等偏下.2.在考查数列求和的同时,将数列与函数、不等式交汇渗透.
02 考点分类 · 析重点
考点一 数列的通项公式
考点二 数列的求和问题
裂项相消法的基本思想就是把通项an分拆成an=bn+k-bn(k≥1,k∈N*)的形式,从而达到在求和时某些项相消的目的,在解题时要善于根据这个基本思想变换数列{an}的通项公式,使之符合裂项相消的条件.
考向2 错位相减法求和(2020·百校联盟联考)已知递增的等比数列{an}的前n项和为Sn,a1+a4=9,a2a3=8.(1)求数列{an}的通项公式;(2)求数列{n·Sn}的前n项和Tn.
应用错位相减法求和的关注点(1)错位相减法适用于求数列{an·bn}的前n项和,其中{an}为等差数列,{bn}为等比数列.(2)在写“Sn”与“qSn”的表达式时,应特别注意将两式“错项对齐”,以便下一步准确地写出“Sn-qSn”的表达式.
(3)公差d大于0的等差数列{an}中,2a7-a13=1,可得2a1+12d-(a1+12d)=1,即a1=1,由a1,a3-1,a6+5成等比数列,可得(a3-1)2=a1(a6+5),即为(1+2d-1)2=1+5d+5,解得d=2(负值舍去),则an=1+2(n-1)=2n-1,n∈N*,所以数列{(-1)n-1an}的前21项和为a1-a2+a3-a4+…+a19-a20+a21=1-3+5-7+…+37-39+41=-2×10+41=21.
(1)以数列为背景的不等式恒成立问题,多与数列求和相联系,最后利用数列或数列对应函数的单调性求解.(2)以数列为背景的不等式证明问题,多与数列求和有关,常转化为数列和的最值问题,同时要注意比较法、放缩法、基本不等式的应用.(3)如果是解不等式,注意因式分解的应用.(4)当已知数列关系式时,需要知道其范围时,可借助数列的单调性,即比较相邻两项的大小即可.
考点三 与数列相关的综合问题
1.求解数列与函数交汇问题注意两点:(1)数列是一类特殊的函数,其定义域是正整数集(或它的有限子集),在求数列最值或不等关系时要特别重视.(2)解题时准确构造函数,利用函数性质时注意限制条件.2.数列为背景的不等式恒成立、不等式证明,多与数列的求和相联系,最后利用数列或数列对应函数的单调性处理.
03 易错清零 · 免失误
1.忽视等比数列中的隐含条件致误各项均为实数的等比数列{an}的前n项和为Sn,若S10=10,S30=70,则S40=______.【错解】 150或-200【剖析】 数列S10,S20-S10,S30-S20,S40-S30的公比q10>0.忽略了此隐含条件,就产生了增解-200.
【解析】 (1)因为点(an+1,Sn)在直线y=x-2上,所以an+1=2+Sn(n∈N*).①当n≥2时,an=2+Sn-1.②①-②,可得an+1-an=Sn-Sn-1=an(n≥2),即an+1=2an(n≥2).当n=1时,a2=2+S1=2+a1,所以a2=4,则a2=2a1.综上,an+1=2an(n∈N*).所以数列{an}是以2为首项,2为公比的等比数列,所以an=2n(n∈N*).
3.用错位相减法求和时对项的位置处理不当(2020·合肥一中10月月考)设等比数列{an}满足a1+a3=20,a2+a4=10.(1)令Tn=a1a2a3…an,求Tn的最大值;(2)令bn=lg2an,求数列{anbn}的前n项和Sn.
【剖析】 运用错位相减法求和的一般步骤为:一是判断模型,如本题中数列{an},{bn}一个为等比数列,一个为等差数列;二是错开位置,如本题的②式,向右错开一个位置来书写,这样为两式相减不会看错项做准备;三是相减,如本题中相减时要注意②式中的最后一项的符号,学生常在此处出错,一定要小心.
04 真题回放 · 悟高考
1.(理)(2020·全国卷Ⅱ卷)数列{an}中,a1=2,am+n=aman,若ak+1+ak+2+…+ak+10=215-25,则k=( )A.2 B.3 C.4 D.5
2.(2020·全国卷Ⅰ卷)数列{an}满足an+2+(-1)nan=3n-1,前16项和为540,则a1=____.【解析】 an+2+(-1)nan=3n-1,当n为奇数时,an+2=an+3n-1;当n为偶数时,an+2+an=3n-1.设数列{an}的前n项和为Sn,
S16=a1+a2+a3+a4+…+a16=a1+a3+a5…+a15+(a2+a4)+…(a14+a16)=a1+(a1+2)+(a1+10)+(a1+24)+(a1+44)+(a1+70)+(a1+102)+(a1+140)+(5+17+29+41)=8a1+392+92=8a1+484=540,∴a1=7.
3.(文)(2020·全国卷Ⅱ卷)记Sn为等差数列{an}的前n项和.若a1=-2,a2+a6=2,则S10=_____.【解析】 ∵{an}是等差数列,且a1=-2,a2+a6=2设{an}等差数列的公差d根据等差数列通项公式:an=a1+(n-1)d可得a1+d+a1+5d=2即:-2+d+(-2)+5d=2整理可得:6d=6
4.(2018·全国卷Ⅰ)记Sn为数列{an}的前n项和.若Sn=2an+1,则S6=_______.
5.(2019·全国卷Ⅲ)记Sn为等差数列{an}的前n项和.若a3=5,a7=13,则S10=______.
6.(理)(2020·全国卷Ⅰ卷)设{an}是公比不为1的等比数列,a1为a2,a3的等差中项.(1)求{an}的公比;(2)若a1=1,求数列{nan}的前n项和.【解析】 (1)设{an}的公比为q,a1为a2,a3的等差中项,∵2a1=a2+a3,a1≠0,∴q2+q-2=0,∵q≠1,∴q=-2.
7.(理)(2020·全国卷Ⅲ卷)设数列{an}满足a1=3,an+1=3an-4n.(1)计算a2,a3,猜想{an}的通项公式并加以证明;(2)求数列{2nan}的前n项和Sn.【解析】 (1)由题意可得a2=3a1-4=9-4=5,a3=3a2-8=15-8=7,由数列{an}的前三项可猜想数列{an}是以3为首项,2为公差的等差数列,即an=2n+1,
证明如下:当n=1时,a1=3成立;假设n=k时,ak=2k+1成立.那么n=k+1时,ak+1=3ak-4k=3(2k+1)-4k=2k+3=2(k+1)+1也成立.则对任意的n∈N*,都有an=2n+1成立.
8.(2019·全国卷Ⅱ)已知{an}是各项均为正数的等比数列,a1=2,a3=2a2+16.(1)求{an}的通项公式;(2)设bn=lg2an,求数列{bn}的前n项和.【解析】 (1)设{an}的公比为q(q>0),由题设得2q2=4q+16,即q2-2q-8=0.解得q=-2(舍去)或q=4.因此{an}的通项公式为an=2×4n-1=22n-1.
9.(2019·全国卷Ⅰ)记Sn为等差数列{an}的前n项和.已知S9=-a5.(1)若a3=4,求{an}的通项公式;(2)若a1>0,求使得Sn≥an的n的取值范围.
新教材适用2024版高考数学二轮总复习第1篇核心专题提升多维突破专题2数列第2讲数列求和及其综合应用课件: 这是一份新教材适用2024版高考数学二轮总复习第1篇核心专题提升多维突破专题2数列第2讲数列求和及其综合应用课件,共60页。PPT课件主要包含了专题二数列,分析考情·明方向,真题研究·悟高考,考点突破·提能力等内容,欢迎下载使用。
2023届高考数学二轮复习专题2第2讲数列求和及其综合应用课件: 这是一份2023届高考数学二轮复习专题2第2讲数列求和及其综合应用课件,共54页。PPT课件主要包含了专题二数列,考情分析,真题热身,感悟高考,考点一数列求和,典例1,典例2,典例3,典例4等内容,欢迎下载使用。
新高考数学二轮复习专题三第2讲数列求和及其综合应用课件: 这是一份新高考数学二轮复习专题三第2讲数列求和及其综合应用课件,共60页。PPT课件主要包含了考情分析,数列求和,考点一,核心提炼,考向1分组转化法,考向2裂项相消法,选择①,当n≥2时,选择②,2求Tn等内容,欢迎下载使用。













