2021-2022学年河北省承德市平泉市七年级（下）期末数学试卷（Word解析版）

这是一份2021-2022学年河北省承德市平泉市七年级（下）期末数学试卷（Word解析版），共21页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
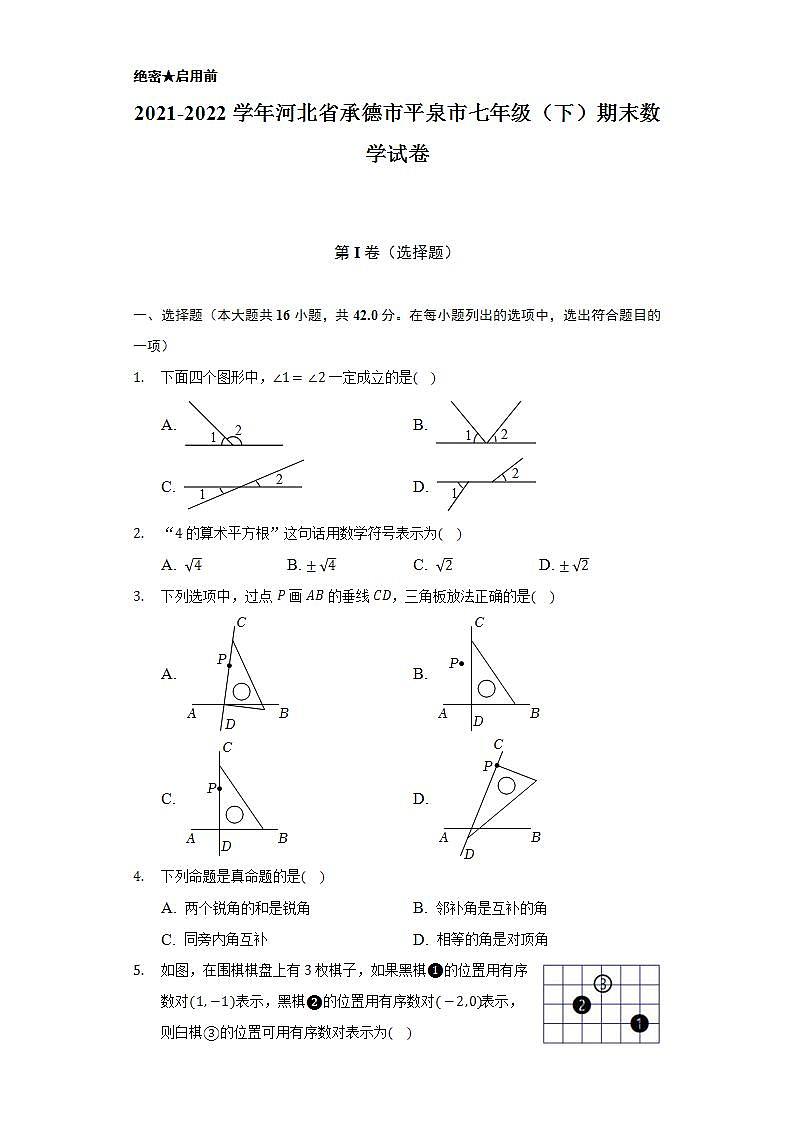
绝密★启用前2021-2022学年河北省承德市平泉市七年级（下）期末数学试卷  第I卷（选择题） 一、选择题（本大题共16小题，共42.0分。在每小题列出的选项中，选出符合题目的一项）下面四个图形中，一定成立的是(    )A.  B.
C.  D. “的算术平方根”这句话用数学符号表示为(    )A.  B.  C.  D. 下列选项中，过点画的垂线，三角板放法正确的是(    )A.  B.
C.  D. 下列命题是真命题的是(    )A. 两个锐角的和是锐角 B. 邻补角是互补的角
C. 同旁内角互补 D. 相等的角是对顶角如图，在围棋棋盘上有枚棋子，如果黑棋的位置用有序数对表示，黑棋的位置用有序数对表示，则白棋的位置可用有序数对表示为(    )
 A.  B.  C.  D. 解二元一次方程组，把代入，结果正确的是(    )A.  B.
C.  D. 某种牛奶包装盒上表明“净重，蛋白质含量”则这种牛奶蛋白质的质量是(    )A. 以上 B.  C. 及以上 D. 不足如图，直线与相交于点，平分，若，则(    )A.
B.
C.
D. 如图，数轴上有，，三点，对应的实数分别为，，以下结论正确的是(    )
A.  B.  C.  D. 如图，在平面直角坐标系中，，两点的坐标分别为，，将线段平移到线段，若点的对应点的坐标为，则的对应点的坐标为(    )
A.  B.  C.  D. 下面是投影屏上出示的抢答题，需要回答横线上符号代表的内容．如图，，求证．
证明：，
．
，
．
．则回答正确的是(    )A. 代表 B. 两直线平行，内错角相等
C. 代表 D. 两直线平行，同位角相等用代入法解方程组有以下过程，其中错误的一步是(    )
由得；
把代入得；
去分母得；
解之得，再由得．A.  B.  C.  D. 某班共有学生人．一天，该班某男生因事请假，当天的男生人数恰为女生人数的一半．若设该班男生人数为，女生人数为，则下列方程组中，能正确计算出、的是(    )A.  B.
C.  D. 如图，若数轴上点，对应的实数分别为和，用圆规在数轴上画点，则点对应的实数是(    )
A.  B.  C.  D. 年月，中共中央、国务院颁布了关于全面加强新时代大中小学劳动教育的意见承德市教育局发布了“普通中小学校劳动教育状况评价指标”为了了解某校学生一周劳动次数的情况，随机抽取若干学生进行调查，得到如图所示的统计图表：

则下列说法正确的是(    )A. 本次调查活动共抽取人
B. 的值为
C. 的值为
D. 扇形统计图中“次”部分所对的圆心角为如图，一块边长为的正方形铁板，在其内部切下一个圆，则这块铁板剩下面积的最小值与下列各数最接近的是(    )A.
B.
C.
D. 第II卷（非选择题） 二、填空题（本大题共3小题，共12.0分）已知，都是有理数，观察表格中的运算，回答下列问题：，的运算运算的结果______；
的算术平方根为______．如图，两个形状、大小完全相同的直角三角形叠放在一起，将直角三角形沿着轴正方向平移到直角三角形的位置．已知点，点，，平移距离为．
点的坐标为______；
阴影部分的面积______．如图，直线，点，是直线上的两个定点，点是直线上的动点．
若，则______；
若点在直线上从左向右运动，则三角形的面积______填“变大”、“变小”、“先变大后变小”、“先变小后变大”或“不变” 三、解答题（本大题共7小题，共66.0分。解答应写出文字说明，证明过程或演算步骤）解二元一次方程组；
解不等式组．如图，，直线分别交直线，于点，，平分交直线于点，．
求的度数；
若将分成两部分，且：：，求的度数．
某商店在第一季度的试销期内，只销售甲、乙两个品牌的洗衣机，共销售台，图一是洗衣机月销量的扇形统计图．

三月份销量占总销量的百分比是______；
根据扇形统计图完成下表：月份

销量合


品牌

一月份

二月份

三月份

四月份甲 乙 合计  在图二中补全表示乙品牌洗衣机月销量的折线统计图；
试销结束后，只能经销一种品牌，该商店应经销哪个品牌的洗衣机？某游客到特产专营店准备购买精加工的豆腐乳和猕猴桃果汁两种盒装特产．若购买盒豆腐乳和盒猕猴桃果汁共需元；购买盒豆腐乳和盒猕猴桃果汁共需元．
请分别求出每盒豆腐乳和每盒猕猴桃汁的价格；
该游客购买了盒豆腐乳和盒猕猴桃汁，共需多少元？如图，已知，．
若，求的度数；
判断与的位置关系，并说明理由；
若平分，求证：平分．
某公司计划购买，两种型号的机器人搬运材料．已知型机器人比型机器人每小时多搬运材料，型机器人用小时搬运的材料与型机器人用小时搬运的材料相等．
求，两种型号的机器人每小时分别搬运多少材料；
该公司计划采购，两种型号的机器人共台，要求每小时搬运材料不得少于，则至少购进型号机器人多少台？如图，在平面直角坐标中有一长方形，点和点的坐标分别为和，点从原点出发，以每秒个单位长度的速度沿着的路线运动到点停止，设点的运动时间为．
点的坐标为______，当时，点的坐标为______；
在点运动过程中，当点到轴的距离为个单位长度时，则点的运动时间为______；
若点出发秒时，点以每秒个单位长度的速度也沿着的路线运动到点停止，求为何值时点，在运动路线上相距的距离为个单位长度？

答案和解析 1.【答案】 【解析】解：、，但与不一定相等，本选项不符合题意；
B、与不一定相等，本选项不符合题意；
C、与是对顶角，一定相等，本选项符合题意；
D、与不一定相等，本选项不符合题意；
故选：．
根据邻补角、对顶角的性质判断即可．
本题考查的是对顶角、邻补角的概念和性质，掌握对顶角相等是解题的关键．
 2.【答案】 【解析】解：的算术平方根为，
故选：．
观察并分析题目从选项中找到的算术平方根，选出正确选项即可．
本题考查了算术平方根的基本性质，关键在于要通过题意正确选出答案．
 3.【答案】 【解析】解：三角板有一个角是直角．
三角板的一条直角边与直线重合．
过点作直线的垂线．
三角板的另一条直角边过点．
符合上述条件的图形只有选项C．
故选：．
根据过直线外一点作已知直线的垂线做法及三角板的特征直接可得．
本题考查了过直线外一点作已知直线的垂线，熟记其做法是解题的关键．
 4.【答案】 【解析】解：、两个锐角的和可能是钝角、直角或锐角，故错误，是假命题，不符合题意；
B、邻补角是互补的角，正确，是真命题，符合题意；
C、两直线平行，同旁内角互补，故错误，是假命题，不符合题意；
D、相等的角不一定是对顶角，故错误，是假命题，不符合题意．
故选：．
利用锐角的定义、邻补角的定义、平行线的性质及对顶角的定义分别判断后即可确定正确的选项．
考查了命题与定理的知识，解题的关键是了解锐角的定义、邻补角的定义、平行线的性质及对顶角的定义，难度不大．
 5.【答案】 【解析】解：建立平面直角坐标系如图，白棋的坐标为．
故选：．
根据黑棋的有序数对确定出坐标原点，然后建立平面直角坐标系，再写出白棋的有序数对即可．
本题考查了坐标确定位置，根据已知点的坐标确定出坐标原点的位置是解题的关键．
 6.【答案】 【解析】【分析】
此题考查了解二元一次方程组，熟练掌握运算法则是解本题的关键．
利用代入消元法计算得到结果，即可作出判断．
【解答】
解：解二元一次方程组，把代入，结果正确的是，
故选：．  7.【答案】 【解析】解：，蛋白质含量，
这种牛奶蛋白质的质量是及以上，
故选：．
根据蛋白质含量大于或等于判断即可．
本题考查了不等式的定义，掌握表示大于或等于是解题的关键．
 8.【答案】 【解析】解：，
，
平分，
，
．
故选：．
由平行线的性质可得，再由角平分线的定义可得，结合平角的定义，即可求的度数．
本题主要考查平行线的性质，解答的关键是熟记平行线的性质：两直线平行，内错角相等．
 9.【答案】 【解析】解：由题图可得，
且．
，．
故选项A错误；
，．
．
．
故选项B错误；
．
．
与互为相反数．
故选项C正确；
由题图可得，．
选项D中错误．
故选：．
根据实数，，在数轴上的位置确定、、的大小，符号，以及绝对值的大小，然后再进行判断．
本题考查了实数与数轴，掌握数轴上右边的数比左边的数大是解题的关键．
 10.【答案】 【解析】解：，两点的坐标分别为，，
点向左平移个单位，向上平移个单位得到点，
，
点向左平移个单位，向上平移个单位得到点，
，
故选：．
利用平移变换的规律解决问题．
本题考查坐标与图形变化平移，解题的关键是掌握平移变换的性质，属于中考常考题型．
 11.【答案】 【解析】证明：，
两直线平行，内错角相等，
，
两直线平行，同旁内角互补
．
故选：．
先根据平行线的性质，得出，且，再求得．
本题主要考查了平行线的性质，解决问题的关键是掌握：两直线平行，内错角相等；两直线平行，同旁内角互补．
 12.【答案】 【解析】解：其中错误的一步为，
正确解法为：去分母得：，
移项合并得：，
解得：．
故选：．
出错一步为，理由去分母时两边都乘以，写出正确的解法即可．
此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．
 13.【答案】 【解析】解：根据该班一男生请假后，男生人数恰为女生人数的一半，得，即；根据某班共有学生人，得．
列方程组为．
故选：．
此题中的等量关系有：
该班一男生请假后，男生人数恰为女生人数的一半；
男生人数女生人数．
列方程组解应用题的关键是找准等量关系，同时能够根据等式的性质对方程进行整理变形，从而找到正确答案．
 14.【答案】 【解析】解：点，对应的实数分别为，．
．
由题图可知，．
．
设点对应的数为．
．
解得．
点对应的数为．
故选：．
由题意可得，，因为，所以，再根据点对应的数，求出点对应的实数．
本题考查了数轴上两个点之间距离的求法，数轴上两个点，对应的实数分别为，，则线段特别的，当点在点的右侧时，．
 15.【答案】 【解析】解：这次调查活动共抽取人，说法错误，不符合题意；
B.，说法错误，不符合题意；
C.，即的值为，说法正确，符合题意；
D.扇形统计图中“次”部分所对的圆心角为：，说法错误，不符合题意．
故选：．
A.根据一周劳动次数次以下的人数和所占的百分比，即可求得本次抽取的人数；
B.用总人数乘以次的人数所占的百分比求出的值，
C.用次及以上的人数除以总人数即可得出的值；
D.用乘以劳动次数为次的人数所占的百分比即可．
本题考查条形统计图、扇形统计图，解答本题的关键是明确题意，利用数形结合的思想解答．
 16.【答案】 【解析】解：依题意当这块铁板剩下面积的取最小值时内部切下的圆最大，
当圆的面积最大的时候圆为正方形的内切圆，
所以圆的直径为正方形的边长，
即圆的半径为，
这块铁板剩下面积的最小值正方形的面积内切圆的面积．
故选：．
首先根据题意得到这块铁板剩下面积的取最小值时内部切下的圆最大，由此得到圆时正方形的内切圆，然后利用正方形的内切圆性质求解．
本题主要考查了正方形的性质，也考查了正方形的内切圆的性质，有一定的综合性．
 17.【答案】   【解析】解：根据表格得：，
得：，
解得：，
得：，
解得：，
则；
故答案为：；
的算术平方根是．
故答案为：．
根据表格列出方程组，求出方程组的解得到与的值，即可求出的值；
求出的算术平方根即可．
此题考查了解二元一次方程组，以及算术平方根，熟练掌握方程组的解法以及算术平方根定义是解本题的关键．
 18.【答案】   【解析】解：，点，
，
平移距离为，
，，
，
，
；
故答案为：；
将直角三角形沿着轴正方向平移到直角三角形的位置，
，
，
梯形的面积阴影部分的面积，


．
故答案为：．
求出，的长度即可得出答案；
根据平移的性质得，从而，梯形的面积阴影部分的面积，求梯形的面积即可得到阴影部分的面积．
本题考查了坐标与图形变化平移，掌握梯形的面积阴影部分的面积是解题的关键．
 19.【答案】  不变 【解析】解：直线，
，
，
，
故答案为：；

点在直线上从左向右运动，则三角形的面积不变，
故答案为：不变．
根据平行线的性质得出，再代入求出答案即可；
根据等底等高的三角形的面积相等得出即可．
本题考查了平行线的性质和三角形的面积，能熟记平行线的性质是解此题的关键，注意：两直线平行，内错角相等，平行线间的距离处处相等．
 20.【答案】解：，
得：，
把代入得：，
解得：，
则方程组的解为；
，
由得：，
由得：，
不等式组的解集为． 【解析】方程组利用加减消元法求出解即可；
分别求出不等式组中两不等式的解集，找出两解集的公共部分即可．
此题考查了解一元一次不等式组，以及解二元一次方程组，熟练掌握各自的解法是解本题的关键．
 21.【答案】解：，，
，
，
平分，
；
：：，
，
，
，
，
，
，
，
，
． 【解析】根据，可得，再根据平角定义和角平分线的定义即可求出的度数；
根据：：，可得，根据，可得，再根据平角定义可得，进而可得的度数．
本题考查了平行线的性质，解决本题的关键是熟练掌握平行线的性质．
 22.【答案】 【解析】解：三月份销量占总销量的百分比是：，
故答案为：；
三月份乙品牌洗衣机月销量为：台，
四月份甲品牌洗衣机月销量为台，
三月份合计销量为：台，
四月份合计销量为：台，

在图二中补全表示乙品牌洗衣机月销量的折线统计图如下：

根据这线统计图可得出：乙洗衣机销售量是上升趋势，甲洗衣机销售量是下降趋势，
故该商店应选择乙洗衣机．
用分别减去其它三个月所占百分比即可；
根据统计图数据解答即可；
根据统计表中提供的数据画图即可；
根据折线统计图，得出两种洗衣机销量的趋势，选择上升趋势的洗衣机即可．
本题考查扇形统计图和折线统计图，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．扇形统计图能清楚地表示出每一部分所占的百分比，折线统计图表示的是事物的变化情况．
 23.【答案】解：设每盒豆腐乳元，每盒猕猴桃果汁元，
可得：，
解得：，
答：每盒豆腐乳元，每盒猕猴桃果汁元；
每盒豆腐乳和每盒猕猴桃果汁的价格分别为元，元，
元，
答：该游客购买了盒豆腐乳和盒猕猴桃果汁，共需元． 【解析】设每盒豆腐乳元，每盒猕猴桃果汁元，根据若购买盒豆腐乳和盒猕猴桃果汁共需元；购买盒豆腐乳和盒猕猴桃果汁共需元，列出方程组，求解即可；
将中的每盒豆腐乳和每盒猕猴桃果汁的价格代入解得即可．
本题考查了二元一次方程组的应用，解答本题的关键是读懂题意，找出合适的等量关系，列方程求解．
 24.【答案】解：，
，
又，
；
．
理由：，
，
又，
，
．
，
．
，
．
平分，
，
．
平分． 【解析】由平行线的性质求得，然后由邻补角的定义求得的度数即可；
由平行线的性质可知：，然后由，再证得，从而可证得；
由可证明，由，可证明，由角平分线的定义可知，，从而可证明．
本题主要考查的是平行线的性质的应用，掌握平行线的性质是解题的关键．
 25.【答案】解：设型机器人每小时搬运千克材料，则型机器人每小时搬运千克材料，根据题意得：
，
解得．
当时，．
答：型机器人每小时搬运千克材料，型机器人每小时搬运千克材料；

设购进型机器人台，则购进型机器人台，根据题意得：
，
解得，
是整数，
，
答：至少购进型机器人台． 【解析】设型机器人每小时搬运千克材料，则型机器人每小时搬运千克材料，根据“型机器人用小时搬运的材料与型机器人用小时搬运的材料相同”建立方程求出其解就可以得出结论；
设购进型机器人台，根据每小时搬运材料不得少于列出不等式并解答．
本题考查了一元一次方程的运用，一元一次不等式的运用，解决问题的关键是读懂题意，找到关键描述语，进而找到所求的量的数量关系．
 26.【答案】    秒或秒 【解析】解：点和点的坐标分别为和，
，，
四边形为长方形，
，，
．
当时，点在线段上，，
，
故答案为：；；
当点在线段上时，
，
点运动的距离为个单位长度，
点从原点出发，以每秒个单位长度的速度运动，
点的运动时间为秒；
当点在线段上时，
，
．
点运动的距离为个单位长度，
点从原点出发，以每秒个单位长度的速度运动，
点的运动时间为秒；
综上，当点到轴的距离为个单位长度时，则点的运动时间为秒或秒，
故答案为：秒或秒；
当点，同在边上时，
，，
，
解得：．
此时点在点处，点在的中点；
再经过秒，点，均在线段上，此时两点的距离均不大于个单位长度；
当点，同在边上时，点在点的前面，
，，
，
解得：，
综上，为秒或秒时，点，在运动路线上相距的距离为个单位长度；
分别求得点，到坐标轴的距离即可得出结论；
利用分类讨论的方法分别得到点到坐标轴的距离即可；
利用分类讨论的方法分两种情况讨论解答：当点，同在边上时，当点，同在边上时，点在点的前面，利用已知条件列出关于的方程，解方程即可求解；
本题主要考查了矩形的性质，坐标系内点的坐标的特征，动点问题，利用点的坐标表示出相应线段的长度是解题的关键．