



人教版九年级上册第二十二章 二次函数综合与测试优秀课后作业题
展开人教版 九年级上册 第22章 单元同步强化测试卷
一.选择题:(30分)
1.已知函数:①y=2x﹣1;②y=﹣2x2﹣1;③y=3x3﹣2x2;④y=2(x+3)2-2x2;⑤y=ax2+bx+c,其中二次函数的个数为( )
A.1 B.2 C.3 D.4
2.抛物线经过两点,若点,点也在抛物线上,且满足,则的大小关系为( )
A. B. C. D.无法确定
3.已知抛物线y=ax2+bx+3中(a,b是常数)与y轴的交点为A,点A与点B关于抛物线的对称轴对称,二次函数y=ax2+bx+3中(b,c是常数)的自变量x与函数值y的部分对应值如下表:
x | … | ﹣1 | 0 | 1 | 3 | 4 | … |
y=ax2+bx+3 | … | 8 |
| 0 | 0 |
| … |
下列结论正确的是( )
A.抛物线的对称轴是x=1 B.当x=2时,y有最大值-1
C.当x<2时,y随x的增大而增大 D.点A的坐标是(0,3)点B的坐标是(4,3)
4.如图,在菱形中,,点从点出发,沿方向匀速运动,过点作交菱形的另一边于点,设点的运动路程为,的面积为,则与之间的函数图象可能为( ).
A.B.C. D.
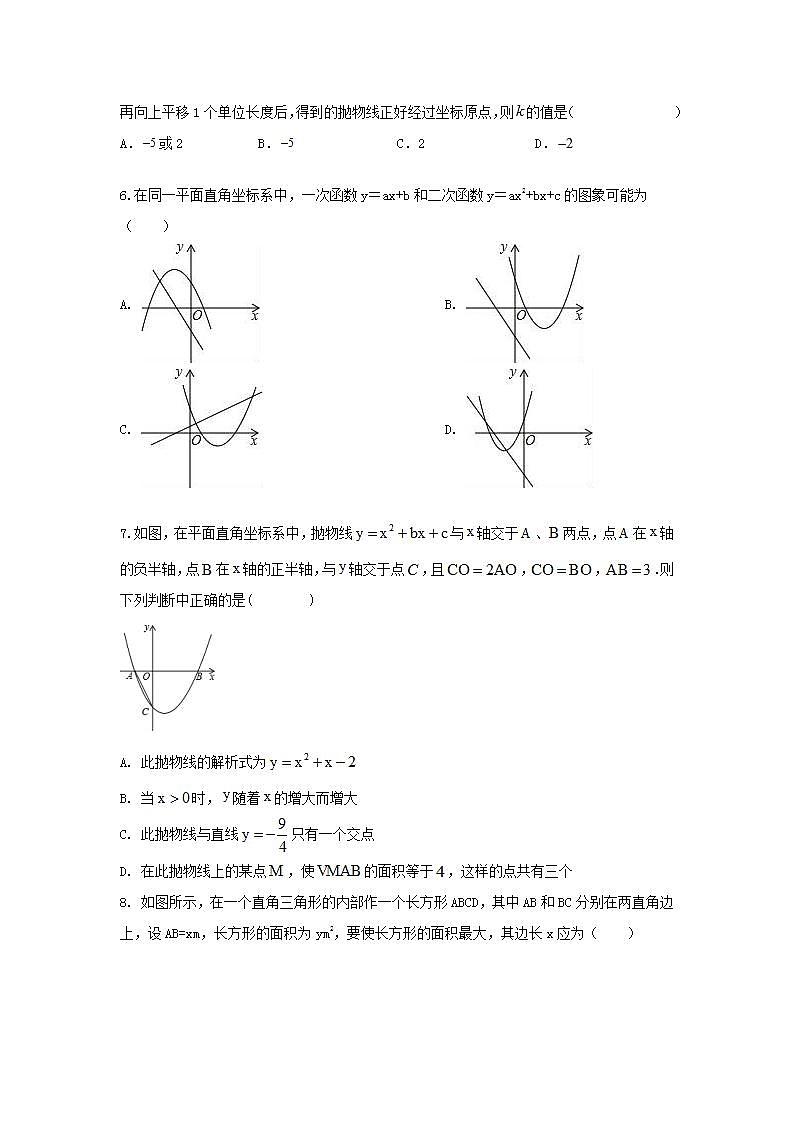
5.已知抛物线的对称轴在轴右侧,现将该抛物线先向右平移3个单位长度,再向上平移1个单位长度后,得到的抛物线正好经过坐标原点,则的值是( )
A.或2 B. C.2 D.
6.在同一平面直角坐标系中,一次函数y=ax+b和二次函数y=ax2+bx+c的图象可能为( )
A. B.
C. D.
7.如图,在平面直角坐标系中,抛物线与轴交于、两点,点在轴的负半轴,点在轴的正半轴,与轴交于点,且,,.则下列判断中正确的是( )
A. 此抛物线的解析式为
B. 当时,随着的增大而增大
C. 此抛物线与直线只有一个交点
D. 在此抛物线上的某点,使的面积等于,这样的点共有三个
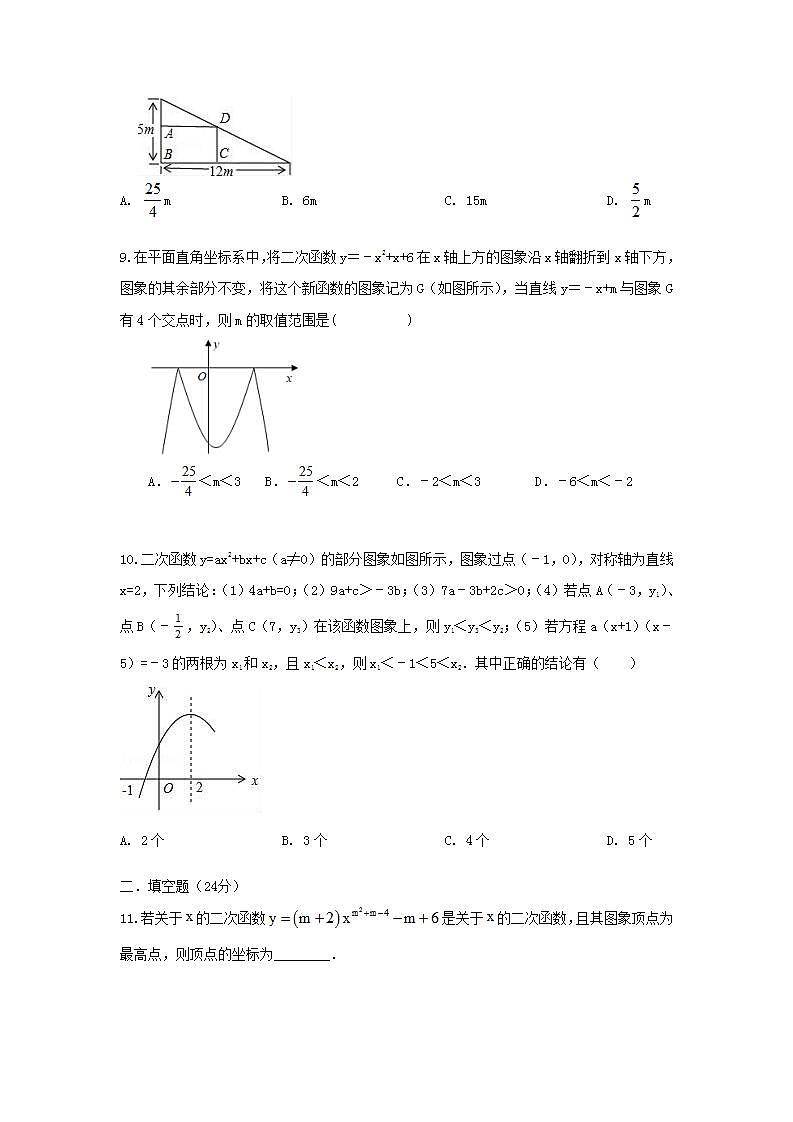
8. 如图所示,在一个直角三角形的内部作一个长方形ABCD,其中AB和BC分别在两直角边上,设AB=xm,长方形的面积为ym2,要使长方形的面积最大,其边长x应为( )
A. m B. 6m C. 15m D. m
9.在平面直角坐标系中,将二次函数y=﹣x2+x+6在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,将这个新函数的图象记为G(如图所示),当直线y=﹣x+m与图象G有4个交点时,则m的取值范围是( )
A.<m<3 B.<m<2 C.﹣2<m<3 D.﹣6<m<﹣2
10.二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>﹣3b;(3)7a﹣3b+2c>0;(4)若点A(﹣3,y1)、点B(﹣,y2)、点C(7,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )
A. 2个 B. 3个 C. 4个 D. 5个
二.填空题(24分)
11.若关于的二次函数是关于的二次函数,且其图象顶点为最高点,则顶点的坐标为________.
12.如图,抛物线y=﹣x2+2x+3与y轴交于点C,点D(0,1),点P是抛物线上的动点.若△PCD是以CD为底的等腰三角形,则点P的坐标为_____.
13.已知y=x2+2kx+k﹣1,当﹣1<x<2时,有最小值﹣1,则k的值为___.
14.如图是二次函数和一次函数的图象,当,的取值范围是________.
15.抛物线的图象如图所示,点A1,A2,A3,A4…,A2022在抛物线第一象限的图象上,点B1,B2,B3,B4...,B2022在y轴的正半轴上,、、…、都是等腰直角三角形,则________.
16.平面直角坐标系中,C(0,4),A为x轴上一动点,连接AC,将AC绕A点顺时针旋转90°得到AB,当点A在x轴上运动时,OB+BC的最小值为_____.
17.(6分)如图为二次函数y=ax2+bx+c(a≠0)的图象根据函数图象,“>”、“=”或“<”填写下列空格:
①a_________0;②4ac﹣b2 _________0;
③2a+b_________0;④a+b+c_________ 0;
⑤当﹣1<x<3时,y_________0;⑥8a+c_________0
18.(8分)如图,直线l过x轴上一点,且与抛物线相交于B、C两点.B点坐标为.
(1) 求抛物线解析式;
(2) 若抛物线上有一点D(在第一象限内),使得,求点D的坐标.
19.(8分)抛物线与x轴交于A、B两点,且点A在点B的左侧,与y轴交于点C,.
(1)求这条抛物线的解析式;
(2)若点与点在(1)中的抛物线上,且.
①求的值;
②将抛物线在下方的部分沿翻折,抛物线的其它部分保持不变,得到一个新图象.当这个新图象与x轴恰好只有两个公共点时,b的取值范围是____________________.
20.(10分)一条单车道的抛物线形隧道如图所示.隧道中公路的宽度AB=8m,隧道的最高点C到公路的距离为6m.
(1)建立适当的平面直角坐标系,求抛物线的表达式;
(2)现有一辆货车的高度是4.4m,货车的宽度是2m,为了保证安全,车顶距离隧道顶部至少0.5m,通过计算说明这辆货车能否安全通过这条隧道.
21.(10分)小红看到一处喷水景观,喷出的水柱呈抛物线形状,她对此展开研究:测得喷水头P距地面0.7m,水柱在距喷水头P水平距离5m处达到最高,最高点距地面3.2m;建立如图所示的平面直角坐标系,并设抛物线的表达式为,其中x(m)是水柱距喷水头的水平距离,y(m)是水柱距地面的高度.
(1)求抛物线的表达式.
(2)爸爸站在水柱正下方,且距喷水头P水平距离3m,身高1.6m的小红在水柱下方走动,当她的头顶恰好接触到水柱时,求她与爸爸的水平距离.
22.(12分)如图,已知抛物线y=ax2+x+c(a≠0)经过原点O,与x轴交于点A(﹣4,0),直线y=x+6交x轴于点B,交抛物线于点C(点C在第三象限).
(1) 求抛物线的解析式;
(2) 若点D是点C关于抛物线对称轴的对称点,连接CD,求CD的长;
(3) 若点P为线段AO上的一个动点,连接PD,以PD为边向右作等边△PDQ.当点P从点A开始向右运动到点O时,点Q移动路径长为______________.
23.(10分)已知抛物线
(1)若抛物线与直线交于(1,0),(5,8)两点.
①求抛物线和直线的函数解析式;
②直接写出当时自变量x的取值范围.
(2)若,线段AB的两个端点坐标分别为A(0,3),B(3,3),当抛物线与线段AB有唯一公共点时,直接写出a的取值范围.
人教版第二十五章 概率初步综合与测试精品同步达标检测题: 这是一份人教版第二十五章 概率初步综合与测试精品同步达标检测题,文件包含答案解析docx、原卷docx等2份试卷配套教学资源,其中试卷共21页, 欢迎下载使用。
2021学年第二十四章 圆综合与测试精品课后复习题: 这是一份2021学年第二十四章 圆综合与测试精品课后复习题,文件包含答案解析docx、原卷docx等2份试卷配套教学资源,其中试卷共31页, 欢迎下载使用。
人教版九年级上册24.3 正多边形和圆优秀课时训练: 这是一份人教版九年级上册24.3 正多边形和圆优秀课时训练,文件包含答案解析docx、原卷docx等2份试卷配套教学资源,其中试卷共28页, 欢迎下载使用。













