
所属成套资源:2022八年级数学上册教案新版华东师大版(42份)
华师大版八年级上册2 利用统计图表传递信息第2课时教学设计
展开
这是一份华师大版八年级上册2 利用统计图表传递信息第2课时教学设计,共7页。教案主要包含了教学重点,教学难点等内容,欢迎下载使用。
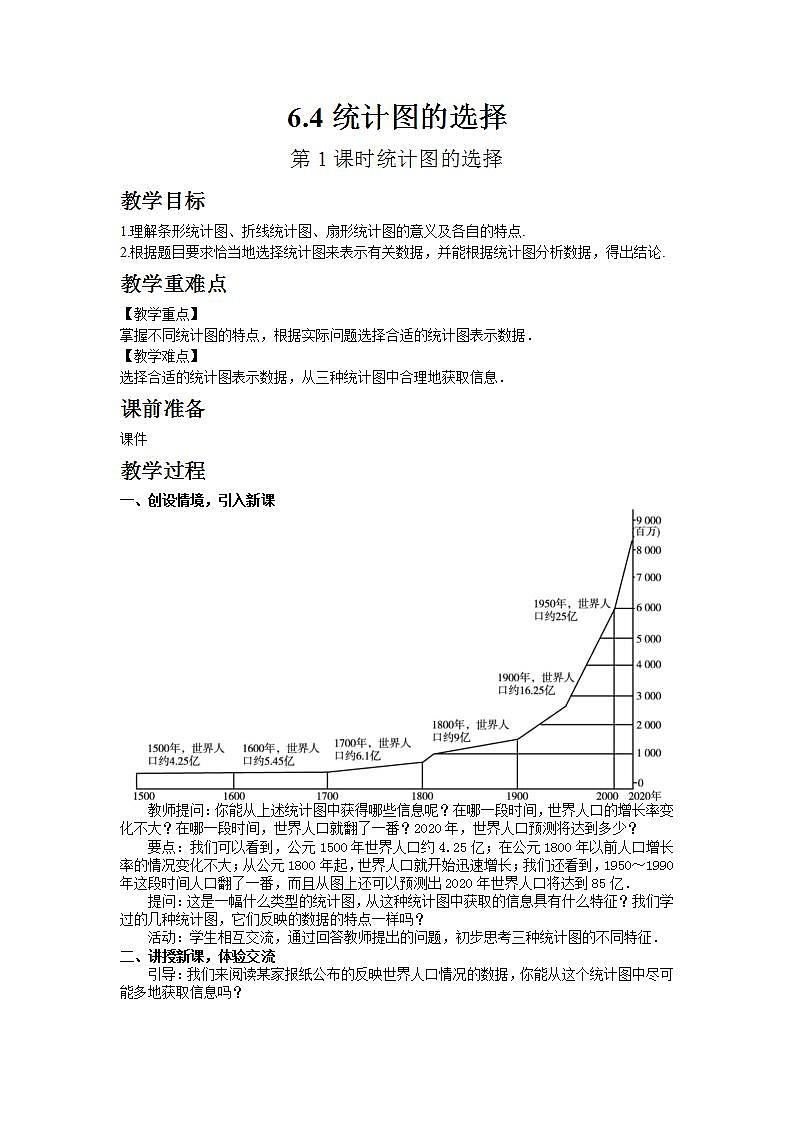
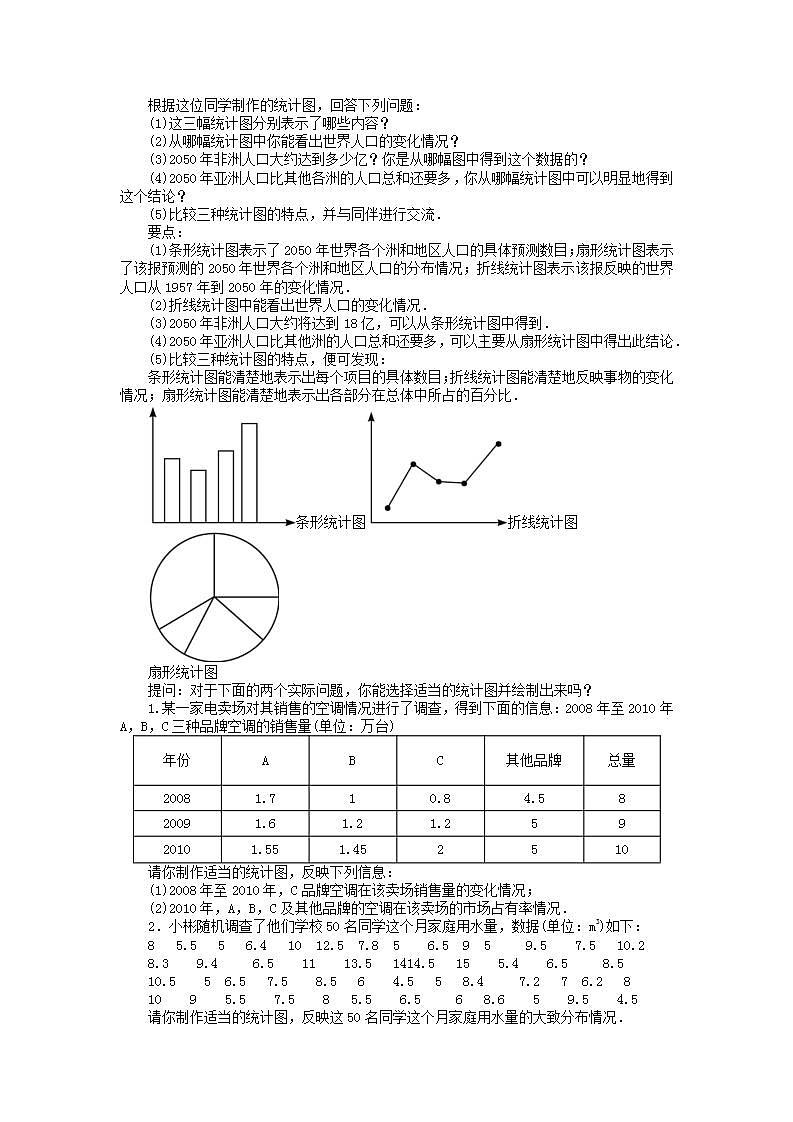
6.4统计图的选择第1课时统计图的选择教学目标1.理解条形统计图、折线统计图、扇形统计图的意义及各自的特点.2.根据题目要求恰当地选择统计图来表示有关数据,并能根据统计图分析数据,得出结论.教学重难点【教学重点】掌握不同统计图的特点,根据实际问题选择合适的统计图表示数据.【教学难点】选择合适的统计图表示数据,从三种统计图中合理地获取信息.课前准备课件教学过程一、创设情境,引入新课教师提问:你能从上述统计图中获得哪些信息呢?在哪一段时间,世界人口的增长率变化不大?在哪一段时间,世界人口就翻了一番?2020年,世界人口预测将达到多少?要点:我们可以看到,公元1500年世界人口约4.25亿;在公元1800年以前人口增长率的情况变化不大;从公元1800年起,世界人口就开始迅速增长;我们还看到,1950~1990年这段时间人口翻了一番,而且从图上还可以预测出2020年世界人口将达到85亿.提问:这是一幅什么类型的统计图,从这种统计图中获取的信息具有什么特征?我们学过的几种统计图,它们反映的数据的特点一样吗?活动:学生相互交流,通过回答教师提出的问题,初步思考三种统计图的不同特征.二、讲授新课,体验交流引导:我们来阅读某家报纸公布的反映世界人口情况的数据,你能从这个统计图中尽可能多地获取信息吗?2050年世界人口预测图活动:讨论交流,获取信息,回答要点如下:2050年世界人口预测图从1957~1974年,世界人口由30亿增加到40亿;从1974~1987年,世界人口由40亿增加到50亿;1987~1999年由50亿增加到60亿;预测1999年~2025年,世界人口从60亿要增加到80亿;2025~2050年25年间预测世界人口增长到90亿,即到2050年,世界人口达到90亿,其中亚洲人口最多,将达到52.68亿,占2050年世界人口的60%.为了更加清晰地表示数据,小明根据上面的相关数据制成了右面的统计图:提问:这是哪种类型的统计图?这位同学是如何制作出这幅统计图的?你能从中得到哪些信息?要点:这位同学是根据统计图上的数据:到2050年亚洲人口达到52.68亿;非洲人口达到17.68亿,拉美及加勒比人口达到8.09亿,欧洲达到8.28亿,北美洲达到3.92亿,得到了2050年世界人口预测的条形统计图.从这个图中可清楚地看到2050年亚洲、非洲、拉美及加勒比地区、欧洲、北美洲的人口预测的具体数目.活动:我们再来看小明制作的另外两个统计图,世界人口变化情况统计图2050年世界人口分布预测图上面的两幅统计图可让学生讨论它们是如何制作的,然后讨论如下问题.根据这位同学制作的统计图,回答下列问题:(1)这三幅统计图分别表示了哪些内容?(2)从哪幅统计图中你能看出世界人口的变化情况?(3)2050年非洲人口大约达到多少亿?你是从哪幅图中得到这个数据的?(4)2050年亚洲人口比其他各洲的人口总和还要多,你从哪幅统计图中可以明显地得到这个结论?(5)比较三种统计图的特点,并与同伴进行交流.要点:(1)条形统计图表示了2050年世界各个洲和地区人口的具体预测数目;扇形统计图表示了该报预测的2050年世界各个洲和地区人口的分布情况;折线统计图表示该报反映的世界人口从1957年到2050年的变化情况.(2)折线统计图中能看出世界人口的变化情况.(3)2050年非洲人口大约将达到18亿,可以从条形统计图中得到.(4)2050年亚洲人口比其他洲的人口总和还要多,可以主要从扇形统计图中得出此结论.(5)比较三种统计图的特点,便可发现:条形统计图能清楚地表示出每个项目的具体数目;折线统计图能清楚地反映事物的变化情况;扇形统计图能清楚地表示出各部分在总体中所占的百分比.条形统计图折线统计图扇形统计图提问:对于下面的两个实际问题,你能选择适当的统计图并绘制出来吗?1.某一家电卖场对其销售的空调情况进行了调查,得到下面的信息:2008年至2010年A,B,C三种品牌空调的销售量(单位:万台)年份ABC其他品牌总量20081.710.84.5820091.61.21.25920101.551.452510请你制作适当的统计图,反映下列信息:(1)2008年至2010年,C品牌空调在该卖场销售量的变化情况;(2)2010年,A,B,C及其他品牌的空调在该卖场的市场占有率情况.2.小彬随机调查了他们学校50名同学这个月家庭用水量,数据(单位:m3)如下:8 5.5 5 6.4 10 12.5 7.8 5 6.5 9 5 9.5 7.5 10.28.3 9.4 6.5 11 13.5 1414.5 15 5.4 6.5 8.510.5 5 6.5 7.5 8.5 6 4.5 5 8.4 7.2 7 6.2 8 10 9 5.5 7.5 8 5.5 6.5 6 8.6 5 9.5 4.5请你制作适当的统计图,反映这50名同学这个月家庭用水量的大致分布情况.活动:讨论交流,根据所获取的信息制作适当的统计图,参考答案如下:1. 某家电卖场2008年至2010年C品牌空调销售量变化统计图(1)2010年A,B,C及其他品牌空调在某家电卖场的市场占有率统计图(2)2.说明:这里的4~6表示大于等于4且小于6,其他类似.三、拓展创新、巩固新知探究点一:统计图的选择要反映某市一周大气中PM2.5的含量变化情况,宜采用()A.条形统计图 B.折线统计图 D.扇形统计图 D.频数直方图解析:因为PM2.5的含量变化没有规律,只能测出不同变化情况,应选折线统计图,故选B.方法总结:要结合三种统计图的缺点进行选择,条形统计图不能反映各部分在总体中的百分比;折线统计图除了不能反映各部分在总体中的百分比外,还不能反映每一部分的具体数量;扇形统计图也不能反映各部分的具体数量.探究点二:统计图的转换某中学七年级(1)班共有学生40人,该班开设了排球、篮球和足球三项体育兴趣课,要求每个学生必须参加,且只能参加其中一项球类运动.图①是小明同学把该班学生报名统计后,绘制成条形统计图的一部分.(1)请你帮小明同学把条形统计图补充完整;(2)请你根据条形统计图中的数据,改用扇形统计图表示出来(如图②);(3)从统计图中你可以获得哪些信息?(写出一条)解析:(1)先求出参加排球兴趣课的人数,进而可补充条形统计图;(2)从条形统计图得出各种兴趣课人数,用它们分别除以40,即可求出相应的百分比,进而可求出相应扇形圆心角度数,画出扇形统计图;(3)答案不唯一,只要合理即可.解:(1)参加排球活动的有40-20-12=8(人),补充图形如图③所示;(2)从条形统计图可知,参加足球活动的有20人,占总人数的百分比为20÷40×100%=50%,圆心角的度数为360°×50%=180°;参加排球活动的有8人,占总人数的百分比为8÷40×100%=20%,圆心角的度数为360°×20%=72°;参加篮球活动的有12人,占总人数的百分比为12÷40×100%=30%,圆心角的度数为360°×30%=108°,扇形统计图如图④所示;(3)答案不唯一,如:该班参加足球活动人数是参加排球活动人数与参加篮球活动人数之和;参加足球活动人数是参加排球活动人数的2.5倍等.方法总结:三种统计图的画法:(1)条形统计图:①画坐标;②确定单位长度;③标出高度,作出条形;(2)折线统计图:①画坐标;②确定单位长度;③描点;④连线(线段);(3)扇形统计图:①计算出总体;②算出各部分百分比;③计算各扇形的圆心角度数;④画扇形,在各部分标明名称、百分比.探究点三:统计图的误导如图所示是2010年~2014年甲、乙两个公司产品销售情况统计图.由统计图可知,销量增速较快的公司是( )A.甲公司 B.乙公司 C.一样快 D.无法确定解析:若横坐标被“压缩”,纵坐标被“放大”,则给人造成统计量的变化速度加快的错觉,反之,就会给人造成统计量的变化速度减慢的错觉.本题两个公司的增速一样快,故选C.方法总结:绘制折线统计图时要注意坐标轴单位长度所表示的量,不要造成直观产生的错觉.探究点四:综合利用不同的统计图中的信息某校为了调查学生视力变化情况,从该校2013年入校的学生中抽取了部分学生进行连续三年的视力跟踪调查,将所得数据处理,制成折线统计图和扇形统计图,如图所示:(1)该校被抽查的学生共有多少名?(2)现规定视力5.1及以上为合格,若被抽查年级共有600名学生,估计该年级在2015年有多少名学生视力合格.解析:由折线统计图可知2015年被抽取的学生人数,且扇形统计图中对应的A区所占的百分比已知,由此即可求出被抽查的学生人数;根据扇形统计图中C、D区所占的百分比,即可求出该年级在2015年有多少名学生视力合格.解:(1)该校被抽查的学生人数为80÷40%=200(人);(2)估计该年级在2015年视力合格的学生人数为600×(10%+20%)=180(人).方法总结:本题的解题技巧在于从两个统计图中获取正确的信息,并互相补充互相利用.例如求被抽查的学生人数时,由折线统计图可知2015年被抽取的学生人数是80人,与其相对应的是扇形统计图中的A区,而A区所占的百分比是40%,由此求出被抽查的学生人数为80÷40%=200(人).四、随堂练习,加强认识2008年5月12日,我国四川汶川发生了里氏8.0级的地震,全国各地纷纷捐款捐物支援灾区.从四川省人民政府每天下午5点举行的新闻发布会上,得到如下信息: 四川省财政收到的抗震救灾专项资金/亿元四川省财政共向灾区调拨救灾应急资金/亿元 中央财政下达救灾专项资金各类捐款合计截至5月18日17.739.1326.8623.97截至5月22日35.8310.9946.8256.02截至5月26日41.8317.0858.9157.5请你制作适当的统计图,反映下列信息:(1)截至5月18日、5月22日、5月26日,四川省财政收到的抗震救灾专项资金的总数情况;(2)截至5月18日、5月22日、5月26日,四川省财政共向灾区调拨救灾应急资金的变化情况;(3)截至5月22日,中央财政下达救灾专项资金和各类捐款在四川省财政收到的专项资金中的比例情况.解:(1)条形统计图截至5月18日、22日、26日四川财政收到的抗震救灾专项资金总数统计图(2)折线统计图截至5月18日、22日、26日四川财政向灾区调拨救灾应急资金变化情况统计图(3)扇形统计图截至5月22日中央财政下达救灾专项资金和各类捐款在四川财政收到的专项资金中的比例统计图五、归纳小结,反思提高三种统计图表示数据的特点,折线统计图一定表示同一对象的发展趋势,不同对象是不能利用折线统计图的;涉及具体数目的一般利用条形统计图;有具体数目但主要关注比例时利用扇形统计图.六、评价与反思教学过程中,应鼓励学生积极参与教学活动,在活动中,体会数学的实用性,从而产生对数学的好奇心和求知欲.七、板书设计
相关教案
这是一份数学八年级上册1 数据有用吗第1课时教案及反思,共3页。教案主要包含了知识与技能,过程与方法,情感态度价值观,教学重点,教学难点等内容,欢迎下载使用。
这是一份初中第15章 数据的收集与表示15.2 数据的表示1 扇形统计图第1课时教学设计,共7页。教案主要包含了知识与技能,过程与方法,情感态度价值观,教学重点,教学难点等内容,欢迎下载使用。
这是一份数学八年级上册2 数据的收集第2课时教案设计,共2页。










