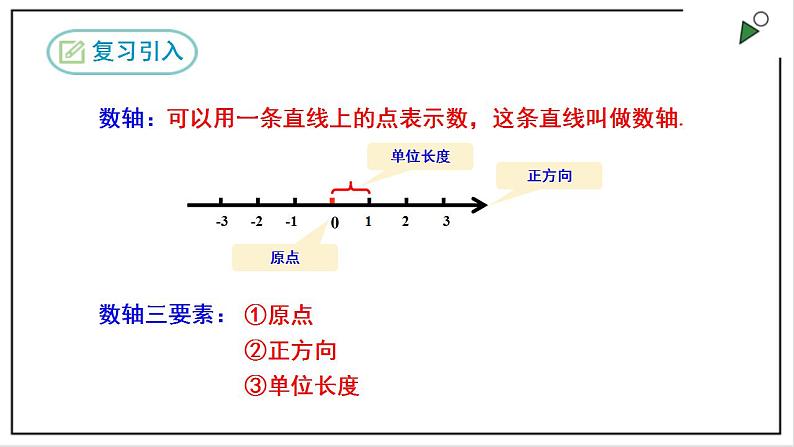
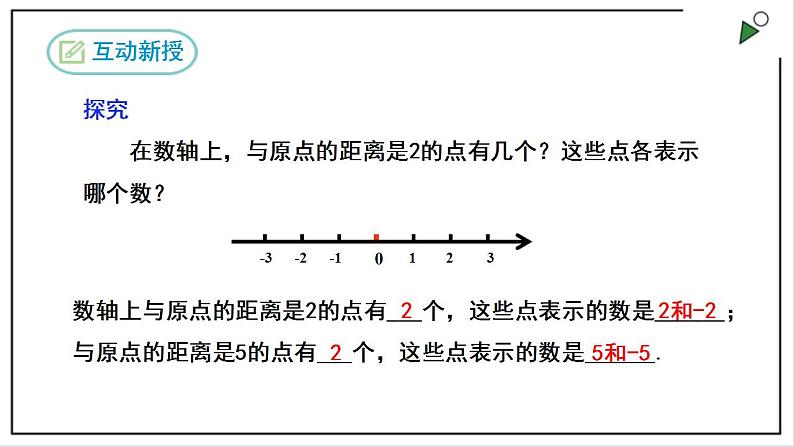
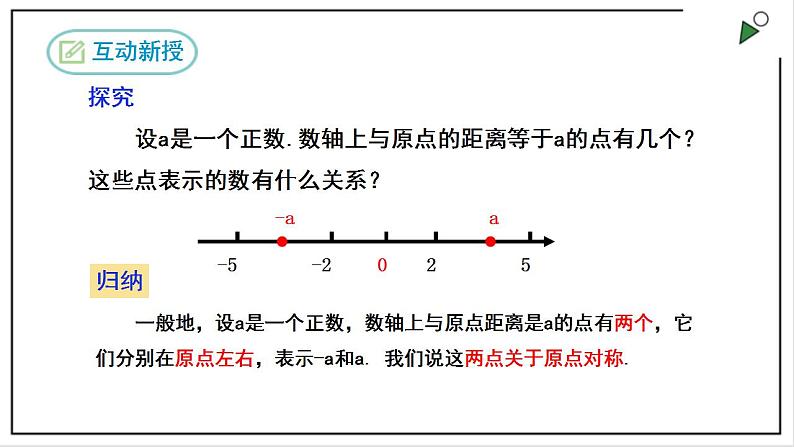
数学七年级上册第一章 有理数1.2 有理数1.2.3 相反数精品ppt课件

1.2.3《相反数》

精选练习

一、单选题

1．（2022·江苏常州·中考真题）2022的相反数是（       ）

A．2022 B． C． D．

【答案】B

【分析】

根据相反数的定义直接求解．

【详解】

解：实数2022的相反数是，

故选：B．

【点睛】

本题主要考查相反数的定义，解题的关键是熟练掌握相反数的定义．

2．（2022·湖南湘潭·中考真题）如图，点、表示的实数互为相反数，则点表示的实数是（       ）

A．2 B．－2 C． D．

【答案】A

【分析】

根据互为相反数的两个数的和为0即可求解．

【详解】

解：因为数轴上两点A，B表示的数互为相反数，点A表示的数是-2，

所以点B表示的数是2，

故选：A．

【点睛】

此题考查了相反数的性质，数轴上两点间的距离，解题的关键是利用数形结合思想解答．

3．（2021·吉林长春·中考真题）的值为（       ）

A． B．2 C． D．

【答案】B

【分析】

根据相反数概念求解即可．

【详解】

化简多重负号，就看负号的个数，此时有两个符号，偶数个则为正，

故选：B．

【点睛】

本题考查了多重负号的化简问题，掌握基本法则是解题关键．

4．（2020·山东淄博·中考真题）若实数a的相反数是﹣2，则a等于（        ）

A．2 B．﹣2 C． D．0

【答案】A

【详解】

解：∵2的相反数是﹣2，

∴a＝2，

故选：A．

5．（2020·湖南郴州·中考真题）如图表示互为相反数的两个点是（ ）

A．点与点 B．点与点 C．点与点 D．点与点

【答案】B

【分析】

根据一个数的相反数定义求解即可．

【详解】

解：在-3，-1,2,3中，3和-3互为相反数，则点A与点D表示互为相反数的两个点．

故选：B．

【点睛】

本题考查了相反数的意义，一个数的相反数就是在这个数前面添上“-”号：一个正数的相反数是负数，一个负数的相反数是正数，0的相反数是0．

6．（2020·山东济宁·中考真题）的相反数是（     ）

A． B． C． D．

【答案】D

【分析】

根据相反数的概念解答即可．

【详解】

解：的相反数是，

故选D.

【点睛】

本题考查了相反数的意义，一个数的相反数就是在这个数前面添上“-”号；一个正数的相反数是负数，一个负数的相反数是正数，0的相反数是0．

二、填空题

7．（2021·山东烟台·期末）若3a+2与－8互为相反数，则a的值为________．

【答案】2

【分析】

根据相反数的性质：互为相反数的两个数的和为列方程求解即可．

【详解】

解：由题意，得，

解得，

故答案为：．

【点睛】

本题考查了一元一次方程，相反数的性质，互为相反数的两个数的和为是解题关键．

8．（2022·河北石家庄·一模）若a，b互为相反数，则（1）______；（2）当，则______．

【答案】     0     或

【分析】

根据相反数的性质计算即可．

【详解】

∵a，b互为相反数，则（1）0，

故答案为：0．

（2）∵，则0-a= -()=，

故答案为：．

【点睛】

本题考查了相反数的性质，熟练掌握相反数的性质是解题的关键．

9．（2022·云南昆明·一模）的相反数是______．

【答案】x

【分析】

根据相反数的定义解答．

【详解】

解：的相反数是x，

故答案为：x．

【点睛】

此题考查了相反数的定义：只有符号不同的两个数叫互为相反数．

10．（2022·广西钦州·七年级期末）相反数等于它本身的数是________．

【答案】0

【分析】

根据相反数的定义，0的相反数仍是0．

【详解】

解：0的相反数是其本身．

故答案为：0．

【点睛】

主要考查相反数的定义，解题的关键是掌握只有符号相反的两个数互为相反数．0的相反数是其本身．

11．若a与b互为相反数，则________．

【答案】1

【分析】

根据相反数的性质可得，代入代数式求解即可．

【详解】

解：∵互为相反数

∴

故答案为：1

【点睛】

本题考查了相反数的性质，掌握互为相反数的两数和为0是解题的关键．

12．（2022·湖南常德·七年级期末）点A在数轴上的位置如图所示，则点A表示的数的相反数是________．

【答案】-3

【分析】

数轴上的点能表示实数，从点在数轴上位置可得出A表示的数．只有符号不同的两个数互为相反数，求一个数的相反数，直接在前面添上“-”号即可，由此可得出本题答案．

【详解】

从图上可知点A表示的数是3，而3的相反数是-3．

故答案为：-3．

【点睛】

本题考察了数轴上的点表示实数和相反数的定义，能正确求已知数的相反数是做出本题的关键．

三、解答题

13．（2022·湖南娄底·七年级期末）已知下列有理数：－4，－2，4，－1，2.5，3

(1)在给定的数轴上表示这些数：

(2)这些数中是否存在互为相反数的两个数？若存在，请指出来，并写出这两个数之间所有的整数；

(3)这些数在数轴上表示的点中是否存在两点之间的距离等于7的两个数？若存在，请指出来．

【答案】(1)见解析

(2)存在，和互为相反数，这两个数之间所有的整数有：－2，－1，0，1，2

(3)存在；－4和3；和

【分析】

（1）将已知数表示在数轴上即可；

（2）根据相反数的定义，找出互为相反数的两个数，并写出这两个数之间的所有整数即可；

（3）根据数轴上两点的距离等于7，即可求得．

(1)

解：将－4，，，－1，2.5，3表示在数轴上，如图所示：

(2)

存在，和互为相反数，这两个数之间所有的整数有：－2，－1，0，1，2．

(3)

存在；

∵，，

∴两点之间的距离等于7的有：－4和3，和．

【点睛】

本题主要考查了用数轴上的点表示有理数，相反数的定义，数轴上两点间的距离，进行数形结合是解题的关键．

14．已知a，b，c为有理数，且它们在数轴上对应点的位置如图所示．

（1）试判断a，b，c的正负性．

（2）在数轴上标出a，b，c的相反数的对应点的位置．

【答案】（1）a＜0，b＞0，c＞0；（2）作图见解析

【分析】

（1）根据数轴的性质分析，即可得到答案；

（2）根据相反数、数轴的性质作图，即可得到答案．

【详解】

（1）结合题意，在原点左侧，b，c在原点右侧

∴a＜0，b＞0，c＞0；

（2）如图所示：

．

【点睛】

本题考查了有理数的知识；解题的关键是熟练掌握相反数、正负数、数轴的性质，从而完成求解．

15．（2021·河北石家庄·七年级阶段练习）化简下列各数：

（1）+（﹣3）；

（2）﹣（+5）；

（3）﹣（﹣3.4）；

（4）﹣[+（﹣8）]；

（5）﹣[﹣（﹣9）]．

【答案】（1）-3；（2）-5；（3）3.4；（4）8；（5）－9

【分析】

多重符号的化简：与“＋”个数无关，有奇数个“−”负，有偶数个“−”号结果为正．

【详解】

解：（1）；

（2）；

（3）；

（4）；

（5）．

【点睛】

本题考查了相反数中多重符号的化简，主要看准“−”号的个数．

16．如果字母a表示一个有理数，那么它的相反数如何表示？如果a的相反数比a大，那么a是什么数？

【答案】；a是负数

【分析】

根据相反数的定义：只有符号不同的两个数叫做互为相反数，知负数的相反数为正数，因为a的相反数比a大，可知a是负数．

【详解】

如果字母a表示一个有理数，那么它的相反数为；

如果a的相反数比a大，即，则a为负数．

【点睛】

本题考查了相反数的定义，敢于用代数式表示有理数及其相反数，正确理解相反数的定义是解决本题的关键．

17．如图所示，已知A，B，C，D四个点在一条没有标明原点的数轴上．

（1）若点A和点C表示的数互为相反数，则原点为　 　；

（2）若点B和点D表示的数互为相反数，则原点为　 　；

（3）若点A和点D表示的数互为相反数，则在数轴上表示出原点O的位置．

【答案】（1）B；（2）C；（3）见解析

【分析】

【详解】

（1）（2）根据相反数的定义可求原点；

（3）根据相反数的定义可求原点，再在数轴上表示出原点O的位置即可．

（1）若点A和点C表示的数互为相反数，则原点为B；

（2）若点B和点D表示的数互为相反数，则原点为C；

（3）如图所示：

故答案为：B；C．

18．写出下列各数的相反数

原数：6，－8，－0.9，，，100，0

【答案】－6，＋8， ＋0.9，，，－100，0

【分析】

【详解】

解：，8，9，，，，0.3

19．如图所示，数轴上的一个单位长度表示2，观察下图，回答问题：

（1）若点与点表示的数互为相反数，则点表示的数是多少？

（2）若点与点表示的数互为相反数，则点表示的数的相反数是多少？

【答案】（1）点表示的数为5；（2）点表示的数的相反数为

【分析】

（1）先确定原点，即可确定点表示的数；

（2）先确定原点，可确定点表示的数，再确定点表示的数的相反数．

【详解】

（1）如图：

∵AD=10，点与点表示的数互为相反数，

∴点表示的数为5；

（2）如图：

∵点与点表示的数互为相反数，

∴点表示的数为2；

∴点表示的数的相反数为．

【点睛】

本题主要考查了数轴和相反数的应用，要注意两点，一是单位长度是多少，二是要注意找好原点，利用原点确定所表示的数．

20．已知数a，b表示的点在数轴上的位置如图所示．

（1）在数轴上表示出a，b的相反数的位置，并将这四个数从小到大排列；

（2）若数b与其相反数相距16个单位长度，则b表示的数是多少？

（3）在（2）的条件下，若数a与数b的相反数表示的点相距4个单位长度，则a表示的数是多少？

【答案】（1）数轴见解析，；（2）-8；（3）4

【分析】

（1）根据相反数的定义作图，再根据数轴右边的数大于左边的数排列即可；

（2）先得到b表示的点到原点的距离为8，然后根据数轴表示数的方法即可确定b表示的数；

（3）先得到-b表示的点到原点的距离为8，再利用数a表示的点与数的相反数表示的点相距4个单位长度，则a表示的点到原点的距离为4，然后根据数轴表示数的方法确定a表示的数．

【详解】

解：（1）a，b的相反数的位置表示如图：

∴；

（2）∵数b与其相反数相距16个单位长度，则b表示的点到原点的距离为8

∴b表示的数是-8；

（3）∵-b表示的点到原点的距离为8，而数a表示的点与数b的相反数表示的点相距4个单位长度

∴a表示的点到原点的距离为8-4=4

∴a表示的数是4．

【点睛】

本题考查了相反数和数轴的应用，灵活应用相反数的定义和数形结合思想是解答本题的关键．

21．（2020·江西宜春·七年级期末）如图，在一条不完整的数轴上一动点向左移动5个单位长度到达点，再向右移动9个单位长度到达点．

（1）①若点表示的数为0，则点、点表示的数分别为：       、       ；

②若点表示的数为1，则点、点表示的数分别为：       、       ；

（2）如果点、表示的数互为相反数，求点表示的数．

【答案】（1）①-5,4；②-3，-8；（2）点B表示的数为-7

【分析】

（1）①根据题意分别列出算式0−5和0−5+9，求得的值分别是点B、点C表示的数；②根据题意分别列出算式1−9+5和1−9，求得的值分别是点B、点A表示的数；

（2）可设点A表示的数为x，则点B、点C表示的数分别为x−5和x+4，根据题意可列出方程x+ x+4=0，求出x，从而可求出x−5，即点B表示的数．

【详解】

解：（1）①因为点表示的数为0，点向左移动5个单位长度到达点，

则有：0−5=−5，

所以点B表示的数为−5，

因为点向左移动5个单位长度到达点，再向右移动9个单位长度到达点，

则有：0−5+9=4，

所以点C表示的数为4；

②因为点表示的数为1，点B向右移动9个单位长度到达点，

所以点C向左移动9个单位长度到达点，

则有：1−9=−8，

所以点B表示的数为−8，

同理可得：−8+5=−3，

所以点A表示的数为−3；

（2）解：设点A表示的数为x，则点B表示的数为x−5，点C表示的数为x+4，

由题意得：x+x+4=0，

解得：x=−2，

则x−5=−7，

所以点B表示的数为−7．

【点睛】

本题考查了数轴、相反数的定义和有理数的运算，解题的关键是根据题意列出算式和方程，题目属于基础题，但容易出错，需要注意数轴上动点的移动方向．

22．（1)化简下列各式：①；②；③；④.

(2)根据(1)中的化简结果，猜想：

①当2019前面有2019个正号时，化简的结果为______；

②当2019前面有2020个负号时，化简的结果为______；

③当2019前面有2019个负号时，化简的结果为______.

【答案】（1）①2019，②-2019,③2019，④-2019；（2）①2019,②2019，③-2019

【分析】

（1）根据相反数的定义分别进行化简即可；

（2）根据（1）的计算结果猜想即可得解．

【详解】

（1)化简各式：①=2019；②=-2019；③=2019；④=-2019.

(2)根据(1)中的化简结果，可得，结果的正负由负号的个数决定：偶正奇负.

①当2019前面有2019个正号时，化简的结果为2019；

②当2019前面有2020个负号时，化简的结果为2019；

③当2019前面有2019个负号时，化简的结果为-2019.

故答案为（1）①2019，②-2019,③2019，④-2019；（2）①2019,②2019，③-2019

【点睛】

本题考查了利用相反数的定义化简，熟记概念并仔细观察化简结果与负号的关系是解题的关键．

23．（2021·江苏·七年级专题练习）操作与探究.对数轴上的任意一点P．

①作出点N使得N和P表示的数互为相反数，再把N对应的点向右平移1个单位，得到点P的对应点P′．我们称P′是P的N变换点；

②把P点向右平移1个单位，得到点M，作出点P′′使得P′′和M表示的数互为相反数，我们称P′′是P的M变换点．

（1）如图，若点P表示的数是－4，则P的N变换点P′表示的数是   ________   ；

（2）若P的M变换点P′′表示的数是2，则点P表示的数是  ________  ；

（3）若P′，P′′分别为P的N变换点和M变换点，且OP′＝2OP′′，求点P表示的数．

【答案】（1）5；（2）-3；（3） 或 ．

【分析】

（1）根据①的操作步骤可得出P′表示的数；

（2）设点P表示的数为x，根据②的操作步骤则-（x+1）=2，得出点P表示的数；

（3）设点P表示的数为y，则P′表示的数是-y+1，P′′表示的数是-（y+1），根据OP′＝2OP′′列方程解出即可得出点P表示的数．

【详解】

解：（1）由①得，若点P表示的数是-4，则点P′表示的数是-（-4）+1=5；

（2）设点P表示的数为x，根据②的操作步骤则-（x+1）=2，

解得：x=-3；

则点P表示的数是-3；

（3）设点P表示的数为y，则P′表示的数是-y+1，P′′表示的数是-（y+1），

∵OP′＝2OP′′，

∴

解得： ， ，

∴点P表示的数是 或 ．

故答案为（1）5；（2）-3；（3） 或 ．

【点睛】

本题考查数轴的知识，注意掌握题意要求的操作步骤，运用方程思想求解．