初中数学人教版七年级上册1.4.1 有理数的乘法优质课课件ppt

这是一份初中数学人教版七年级上册1.4.1 有理数的乘法优质课课件ppt，文件包含141有理数的乘法练习解析版docx、141有理数的乘法练习原卷版docx、141有理数的乘法第二课时pptx等3份课件配套教学资源，其中PPT共0页， 欢迎下载使用。
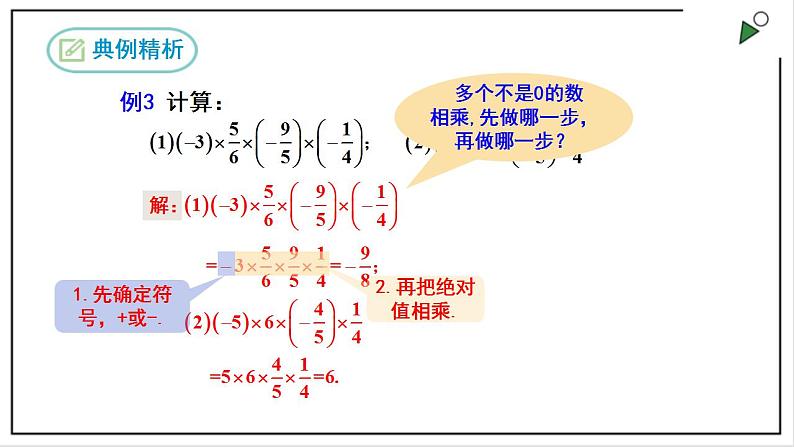
1.4.1《有理数的乘法》精选练习一、单选题1．（2022·湖南·中考真题）的倒数是（       ）A．2022 B． C． D．【答案】D【分析】根据倒数定义解答．【详解】解：-2022的倒数是，故选：D．【点睛】此题考查了倒数的定义，熟记定义是解题的关键．2．（2022·浙江台州·中考真题）计算的结果是（       ）A．6 B． C．5 D．【答案】A【分析】根据有理数乘法法则计算即可．【详解】解：．故选：A．【点睛】本题考查了有理数乘法：两个数相乘，同号得正，异号得负，再将两个数字的绝对值相乘．3．（2021·广西百色·一模）下列说法①若，则、互为相反数；②若，则、互为倒数；③若，则、均大于；④若，则一定为正数，其中正确的为(       )A．①④ B．①② C．①②④ D．①③④【答案】B【分析】分别利用有理数的加法、相反数的定义，倒数的定义、有理数乘法运算，绝对值的性质分别分析得出答案．【详解】解：若，则、互为相反数是正确的；若，则、互为倒数是正确的；若，则、均大于或均小于，题干的说法是错误的；若，则一定为非负数，题干的说法是错误的．∴正确的有①②，故选：B．【点睛】此题主要考查了相反数、倒数的定义、有理数的乘法运算，绝对值的性质等知识，正确掌握相关性质是解题关键．4．（2022·浙江丽水·三模）如图，运算中的（       ）处，填写的理由是（       ）（乘法交换律）（                 ）． A．乘法交换律 B．乘法结合律 C．分配律 D．加括号【答案】B【分析】根据运算过程可知是根据乘法结合律．【详解】解： (乘法交换律)(乘法结合律) 故选：B．【点睛】本题考查了有理数的乘法运算律，熟练掌握和运用有理数的乘法运算律是解决本题的关键．5．（2022·山东济南·一模）实数a，b在数轴上对应点位置如图所示，则下列不等式正确的是（       ）A． B． C． D．【答案】C【分析】由题意可知a＜b＜0，故a、b同号，且|a|＞|b|．根据有理数加减法乘除法法则可推断出各式的符号．【详解】解：由题意可知a＜b＜0，故a、b同号，且|a|＞|b|．∴＞0，a-b=a+|b|＜0，ab＞0，a+b＜0；∴选项A、B、D错误，选项C正确，故选：C．【点睛】此题主要考查了不等式的基本性质和实数和数轴的基本知识点，比较简单．6．（2020·江西景德镇·七年级期中）下面是关于0的一些说法，其中正确说法的个数是（       ）①0既不是正数也不是负数；②0的绝对值最小；③0是最小的整数；④0的绝对值、相反数、倒数都是它本身．A．0 B．1 C．2 D．3【答案】C【分析】根据有理数的分类，绝对值，相反数，倒数的定义逐一判断即可．【详解】解：①0既不是正数也不是负数，说法正确，符合题意；②0的绝对值最小，说法正确，符合题意；③0不是最小的整数，说法错误，不符合题意；④0的绝对值、相反数都是它本身，0没有倒数，说法错误，不符合题意；∴说法正确的一共有2个，故选C．【点睛】本题主要考查了有理数的分类，绝对值，相反数和倒数，熟知相关定义是解题的关键．二、填空题7．（2022·江苏南京·一模）-的绝对值是 _____相反数是 ______倒数是 ______【答案】               【分析】根据绝对值是数轴上的点到原点的距离，只有符号不同的两个数互为相反数，乘积为1的两个数互为倒数，可得答案．【详解】解：-的绝对值是；相反数是，倒数是-．故答案为：，，．【点睛】本题主要考查的是倒数、相反数、绝对值的定义，熟练掌握相关概念是解题的关键．8．如果a＜0，b＞0，那么ab____0．【答案】＜【分析】根据有理数乘法法则，同号为正，异号为负，进行判断即可．【详解】解：∵a＜0，b＞0，∴ab＜0，故答案为：＜．【点睛】本题考查了有理数乘法运算法则，正确理解有理数乘法运算法则是解题的关键．9．若﹣2减去一个有理数的差是﹣5，则﹣2乘这个有理数的积是 ____．【答案】【分析】先根据减数等于被减数减去差求出这个数，再根据有理数的乘法运算法则进行计算即可得解．【详解】解：﹣2﹣（﹣5）＝﹣2+5＝3，﹣2×3＝﹣6，故答案为：﹣6．【点睛】本题主要考查了有理数的减法，有理数的乘法，是基础题，熟记运算法则是解此题的关键，难点在于求出这个数．10．在2，﹣3，4，﹣5这四个数中，任取两个数相乘，所得的积最大是______．【答案】15【分析】两个数相乘，同号得正，异号得负，且正数大于一切负数，所以找积最大的应从同号的两个数中寻找即可．【详解】解：2×4＝8，（﹣3）×（﹣5）＝15，15＞8．∴积最大是15．故答案为：15．【点睛】本题主要考查的知识点是有理数的乘法及有理数大小比较，关键要明确不为零的有理数相乘的法则：两数相乘，同号得正，异号得负，并把绝对值相乘．11．计算：﹣99×18＝______．【答案】﹣1799【详解】利用乘法分配律计算，即可求解．解：原式＝（﹣100+）×18，＝﹣100×18+×18，＝﹣1800+1，＝﹣1799故答案为：﹣1799【点睛】本题主要考查了有理数的乘法运算律，熟练掌握有理数的乘法运算律是解题的关键．12．已知，且a、b、c都不等于零，那么a、b、c三个数中，_______最大，_______最小．【答案】     a     b【分析】求出a、b、c的比值即可判断大小．【详解】解：∵，∴a：b＝7：5，∵，∴b：c＝5：6，∴a：b：c＝7：5：6，故a最大，b最小，故答案为：a，b．【点睛】本题考查有理数的乘法，解题的关键是求出a：b：c的值，本题属于基础题型．三、解答题13．（﹣8）×4×（﹣1）×（﹣3）．【答案】【分析】根据有理数的乘法法则即可求出．【详解】解：（﹣8）×4×（﹣1）×（﹣3）＝﹣（8×4×1×3）＝﹣96．【点睛】本题主要考查了有理数的乘法，熟练掌握有理数的乘法法则是解决此题的关键．14．（2020·河北保定·一模）计算下列各式的值．（1）（﹣53）+（+21）﹣（﹣69）﹣（+37）（2）﹣3.61×0.75+0.61×+（﹣0.2）×75%．【答案】（1）0；（2）-2.4【分析】（1）根据有理数的加减运算法则，先省略括号，再进行计算即可得解；（2）逆运用乘法分配律进行计算即可得解．【详解】解：（1）（﹣53）+（+21）﹣（﹣69）﹣（+37）＝﹣53+21+69﹣37＝﹣90+90＝0；（2）＝﹣3.61×0.75+0.61×0.75+（﹣0.2）×0.75＝0.75×（﹣3.61+0.61﹣0.2）＝0.75×（﹣3.2）＝﹣2.4．【点睛】本题考查了有理数的乘法，有理数的加减混合运算，熟记运算法则是解题的关键，（2）利用运算定律可以使计算更加简便．15．已知，|a|＝3，|b|＝2，且ab＞0，求a﹣b的值．【答案】a﹣b=1或-1【分析】直接利用绝对值的性质得出a，b的值，进而得出答案．【详解】解：∵|a|＝3，|b|＝2，∴a＝±3，b＝±2，∵ab＞0，∴a＝3时，b＝2；a＝﹣3时，b＝﹣2，故a﹣b＝3﹣2＝1或a﹣b＝﹣3﹣（﹣2）＝﹣1．【点睛】此题主要考查了有理数的乘法以及绝对值，正确得出a、b的值是解题关键．16．（2021·云南·景谷傣族彝族自治县教育体育局教研室七年级期末）在我市创建“卫生城市”过程中，某天市交警大队的一辆警车在东西方向的街上巡视，警车从某广场A处出发，规定向东方向为正，当天行驶纪录如下（单位：千米）：，，，，，，，．(1)最后警车是否回到广场A处？若没有，在广场A处何方？距广场A处多远？(2)若警车行驶1千米耗油0.2升，出发时油箱中有油8升，问在当天巡视中，油箱中的油够不够？若不够，途中还需补充多少升油？【答案】(1)没有；西方；5千米(2)不够；4.6升【分析】（1）将各数相加即可确定警车所在的方向及距离；（2）将所有路程相加，然后乘以每千米油耗，最后进行加减计算即可．(1)没有，（千米）．答：警车在广场A的西方，距广场A处5千米处．(2)（千米），（升）（升）．答：途中还需补充4.6升．【点睛】题目主要考查正负数的意义及有理数的加减运算及乘法运算的应用，理解题意是解题关键．17．（2022·江西吉安·七年级期末）某汽车制造厂计划每周生产400辆新能源汽车，由于工人实行轮休，每日上班人数不一定相等，实际每日产量与计划量相比情况如下表（增加的车辆数为正数，减少的车辆数为负数）：星期一二三四五六日增减（辆）+15+17-2+11+14-15-12 (1)本周实际产量与计划产量相比，是增加了还是减少了？是多少？(2)若生产此款新能源汽车每辆利润约为0.2万元，求本周该厂家生产车辆的总利润．【答案】(1)本周实际产量与计划产量相比，是增加了，本周的实际产量为428辆车(2)本周该厂家生产车辆的总利润是85.6万元【分析】（1）把这七天的数据相加，如果结果为正则实际产量产量增加，如果结果为负，则实际产量减小，然后根据计划每天产量为400辆求出实际产量即可；（2）根据利润=单件利润×数量求解即可．(1)解：∵，∴本周实际产量与计划产量相比，是增加了，∵，∴本周的实际产量为428辆车；(2)解：万元，∴本周该厂家生产车辆的总利润是85.6万元．【点睛】本题主要考查了有理数混合计算的应用，有理数乘法的应用，有理数加法的应用，正确理解题意是解题的关键．18．（2020·黑龙江齐齐哈尔·期中）某品牌的微波炉搞促销活动，在甲商场每满200元减40元，在乙商场打八折出售．妈妈要买一台标价为450元的这种微波炉．在甲、乙哪个商场买合算？【答案】在乙商场买合算【分析】根据促销活动得到两个商场买一台标价为450元的微波炉钱数，比较大小即可求解．【详解】甲商场450-40×2=370（元）乙商场450×80%=360（元）360元＜370元答：在乙商场买合算【点睛】考查了有理数的混合运算，关键是理解两个商场的促销活动的规则． 19．（2020·广东·东莞市东城中学七年级期中）小明妈妈在某玩具厂工作，厂里规定每个工人生产某种玩具，原计划每天生产20个，但由于种种原因，实际每天生产个数与原计划每天生产个数相比有出入．下表是小明妈妈十天内的生产情况记录表（超过记为正、不足记为负）：天数12214增、减产值+6﹣7﹣4+5﹣1 (1)与原计划相比，小明妈妈十天生产玩具总计超过或不足多少个？(2)该厂实行“每日计件工资制”，每生产一个玩具可得工资5元，求小明妈妈这十天的工资总额是多少元？【答案】(1)司机最后在原地的东边，离原地3千米(2)925元【分析】（1）根据有理数的加法运算法则和乘法运算法则列式计算即可；（2）用小明妈妈十天生产玩具的总数乘5即可．【详解】解：（1）（+6）×1+（﹣7）×2+（﹣4）×2+（+5）×1+（﹣1）×4＝﹣15（个）， 故与原计划相比，小明妈妈十天生产玩具总计不足15个；（2）5×（20×10﹣15）＝925（元）．故小明妈妈这一周的工资总额是925元．【点睛】本题主要考查了正负数的意义以及有理数的混合运算，理解正负数的意义是解答此题的关键．20．（2020·河南·焦作市第十八中学七年级阶段练习）观察下列等式＝1﹣，＝﹣，＝﹣，将以上三个等式两边分别相加得++＝1﹣+﹣+﹣＝1﹣＝．（1）猜想并写出     ；（2）+++…+＝     ；（3）探究并计算：；（4）计算：．【答案】（1）；（2）；（3）；（4）．【分析】（1）观察已知等式，进行归纳类推即可得；（2）根据（1）中的猜想进行计算即可得；（3）先根据乘法分配律提取，再参照（2）进行计算即可得；（4）先根据乘法分配律提取，再参照（2）进行计算即可得．【详解】（1），，，归纳类推得：，故答案为：；（2），，，，故答案为：；（3），，，，，；（4），，，，，，．【点睛】本题考查了有理数乘法与加减法的规律性问题，依据题意，正确归纳类推出一般规律是解题关键．21．（2021·江西·新余市第一中学七年级阶段练习）从2开始，连续的偶数相加，它们的和的情况如下表：加数m的个数和S12＝1×222+4＝6＝2×332+4+6＝12＝3×442+4+6+8＝20＝4×552+4+6+8+10＝30＝5×6 （1）按这个规律，当m＝6时，和S为　   　；（2）从2开始，m个连续偶数相加，它们的和S与m之间的关系，用公式表示出来为：S＝　   　．（3）应用上述公式计算：①2+4+6+…+100②1002+1004+1006+…+1100③1+3+5+7+…+99【答案】（1）；（2）；（3）①；②；③．【分析】（1）根据规律列出运算式子，计算有理数的乘法即可得；（2）根据表格归纳类推出一般规律即可得；（3）①根据（2）的结论列出运算式子，计算有理数的乘法即可得；②利用的值减去的值即可得；③将运算中的每个加数都加上1可变成（3）①的运算式子，再减去50即可得．【详解】（1）根据规律得：当时，和，故答案为：42；（2）由表可知，当时，，当时，，当时，，当时，，归纳类推得：，故答案为：；（3）①，，；②，，，，，；③，，，，．【点睛】本题考查了有理数加减法与乘法的规律型问题，正确归纳类推出一般规律是解题关键．22．有张写着不同数字的卡片：，，，，，，如果从中任意抽取张．使这张卡片上的数字的积最小，应该如何抽？积又是多少？使这张卡片上的数字的积最大，应该如何抽？积又是多少？【答案】(1) 抽数据、、,最小值－80；（2）抽数据；；，最大值120【分析】(1)根据几个不等于0的数相乘，积的符号由负因数的个数决定，当负因数有奇数个时，积为负可得应该抽取抽数据-8、5、2；(2) 几个不等于0的数相乘，积的符号由负因数的个数决定，当负因数有偶数个时，积为正可得抽数据-8、-3、5.【详解】解：抽数据、、；；抽数据；；，．【点睛】此题主要考查了有理数的乘法，关键是掌握多个有理数相乘的法则.23．（2021·北京市第一六一中学七年级期中）在数轴上，点A向右移动1个单位得到点B，点B向右移动（n+1）（n为正整数）个单位得到点C，点A，B，C分别表示有理数a，b，c．（1）当n＝1时，①点A，B，C三点在数轴上的位置如图所示，a，b，c三个数的乘积为正数，数轴上原点的位置可能 ．A．在点A左侧或在A，B两点之间   B．在点C右侧或在A，B两点之间C．在点A左侧或在B，C两点之间   D．在点C右侧或在B，C两点之间②若这三个数的和与其中的一个数相等，求a的值；（2）将点C向右移动（n+2）个单位得到点D，点D表示有理数d，a、b、c、d四个数的积为正数，这四个数的和与其中的两个数的和相等，且a为整数，请用含n的代数式表示a．【答案】（1）①C；②a的值为或或；（2）当为奇数时，，当为偶数时，．【分析】（1）①把代入即可得出，，再根据、、三个数的乘积为正数即可选择出答案；②分三种情况逐个计算即可求得答案；（2）分两种情况讨论：当为奇数时；当为偶数时；用含的代数式表示即可．【详解】解：（1）①把代入即可得出，，、、三个数的乘积为正数，从而可得出原点在点左侧或在、两点之间．故选：C；②由题意可得：，，当时，则，当时，则，当时，则，综上所述：a的值为或或；（2）依据题意得，，，．、、、四个数的和与其中的两个数的和相等，∴这个四个数中有两个数互为相反数，又、、、这四个数的积为正数， ∴、为负数，、为正数，原点在之间，或或和，当时，由于，即，原点在、之间，不合题意舍去；当时，由于，原点在上，不合题意舍去，或，或，或；为整数，当为奇数时，，当为偶数时，．【点睛】本题考查了数轴的应用、有理数的乘法，把数和点对应起来，也就是把“数”和“形”结合起来，二者互相补充，相辅相成，把很多复杂的问题转化为简单的问题，在学习中要注意培养数形结合的数学思想．