初中数学1 用树状图或表格求概率优秀课件ppt

这是一份初中数学1 用树状图或表格求概率优秀课件ppt，文件包含311《用树状图或表格求概率》课件PPTpptx、311《用树状图或表格求概率》教案docx等2份课件配套教学资源，其中PPT共16页， 欢迎下载使用。
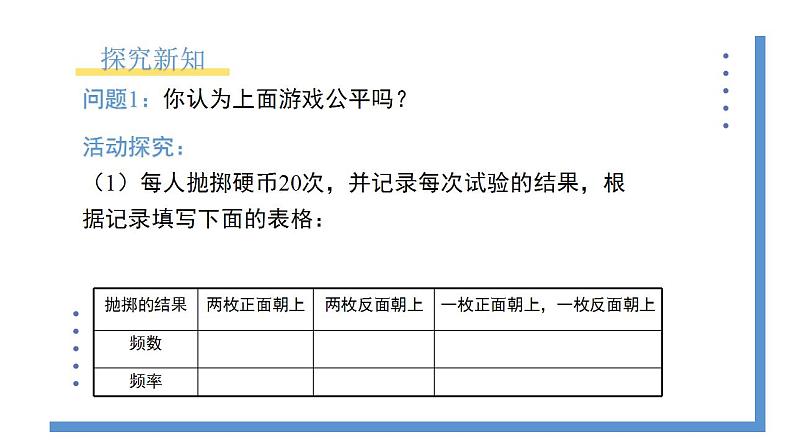
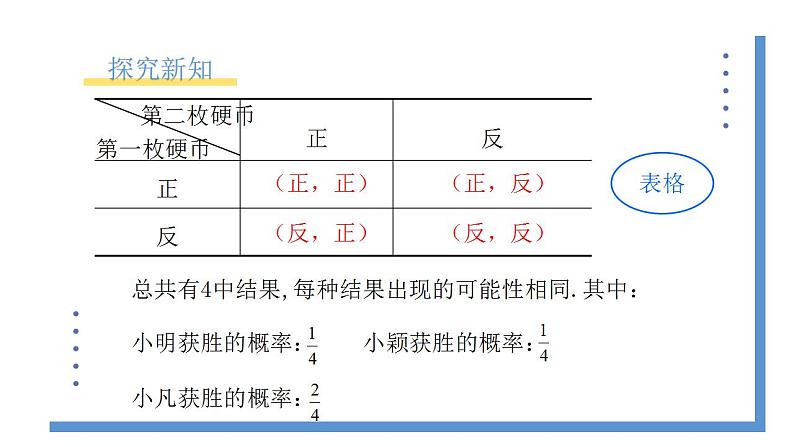
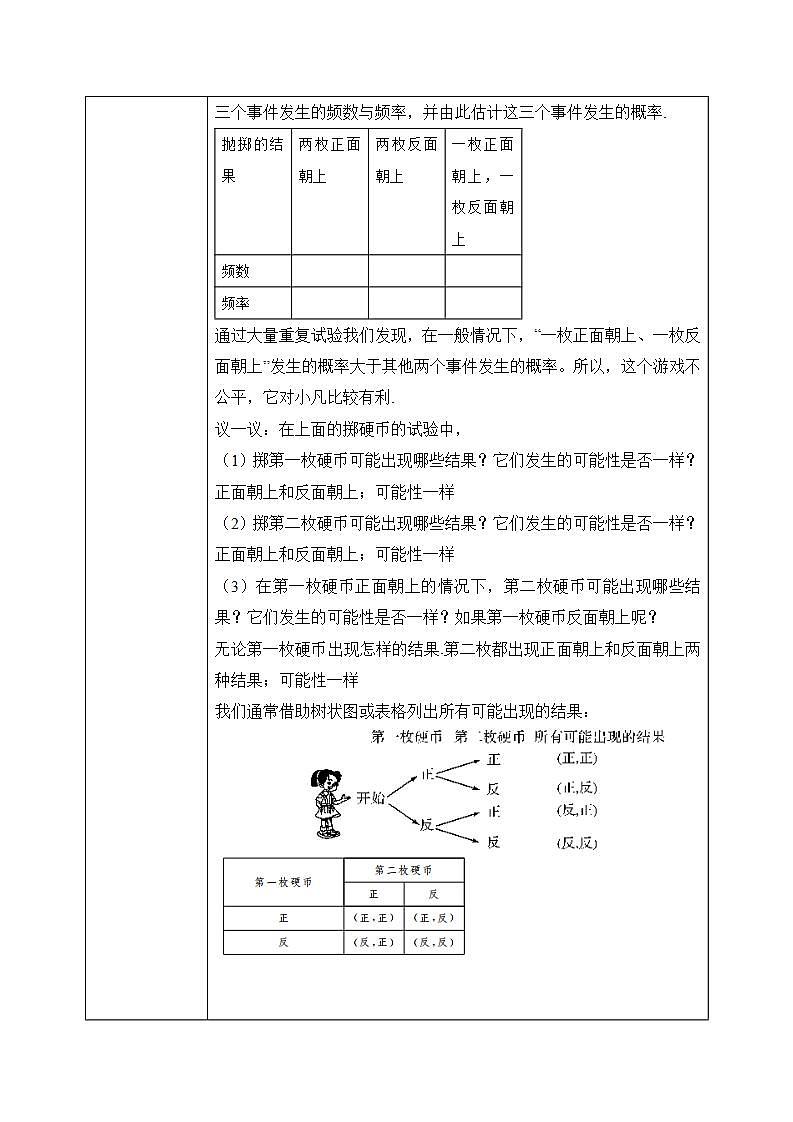
北师大版数学九年级上册《3.1.1用树状图或表格求概率》教学设计课题名3.1.1用树状图或表格求概率教学目标1.经历猜测、试验、收集试验数据、分析试验结果等活动过程，进一步体验数据的随机性，积累数学活动经验．2．会用列表或画树状图等方法计算简单事件发生的概率.3.会通过试验进一步感受随机事件发生的频率的稳定性，理解事件发生的频率与概率的关系.教学重点用列表或画树状图等方法计算简单事件发生的概率.教学难点用列表或画树状图等方法列举简单事件发生的所有结果.教学准备教师准备：熟悉课本和课件.学生准备：复习概率与统计的相关知识.教学过程一、复习1.什么叫事件的概率？2.一般地，如果在一次试验中有n种可能结果，并且它们发生的可能性都相等，事件A包含其中的m种结果，那么事件A发生的概率P（A）= 二、探究新知小明、小颖和小凡都想去看周末电影，但是只有一张电影票，三人决定一起做游戏，谁获胜谁就去看电影.游戏规则如下：     连续掷两枚质地均匀的硬币，若两枚正面朝上，则小明获胜；若两枚反面朝上，则小颖获胜；若一枚正面朝上、一枚反面朝上，则小凡获胜.   师：这个游戏公平吗？连续掷两枚质地均勺的硬币, “两枚正面朝上” “两枚反面朝上” "一枚正面朝上、一枚反面朝上”这三个事件发生的概率相同吗?合作交流：分小组进行试验，然后累计各组的试验数据，分别计算这三个事件发生的频数与频率，并由此估计这三个事件发生的概率.抛掷的结果两枚正面朝上两枚反面朝上一枚正面朝上，一枚反面朝上频数   频率   通过大量重复试验我们发现，在一般情况下，“一枚正面朝上、一枚反面朝上”发生的概率大于其他两个事件发生的概率。所以，这个游戏不公平，它对小凡比较有利.议一议：在上面的掷硬币的试验中，（1）掷第一枚硬币可能出现哪些结果？它们发生的可能性是否一样？正面朝上和反面朝上；可能性一样（2）掷第二枚硬币可能出现哪些结果？它们发生的可能性是否一样？正面朝上和反面朝上；可能性一样（3）在第一枚硬币正面朝上的情况下，第二枚硬币可能出现哪些结果？它们发生的可能性是否一样？如果第一枚硬币反面朝上呢？无论第一枚硬币出现怎样的结果.第二枚都出现正面朝上和反面朝上两种结果；可能性一样我们通常借助树状图或表格列出所有可能出现的结果：        通过观察树状图或者是表格你能发现什么？掷硬币的试验总共有4种结果，每种结果出现的可能性相同.    （正，正）出现了______次，所以小明获胜的概率是_______；（反，反）出现了______次，所以小颖获胜的概率是_______；（正，反）出现了______次，所以小凡获胜的概率是_______.总结归纳利用树状图或表格，我们可以不重复、不遗漏地列出所有可能的结果，从而比较方便地求出某些事件发生的概率.求概率的“四个步骤”：1.定:确定该试验的几个步骤、顺序、每一步可能产生的结果.2.画:列举或画树状图每一环节可能产生的结果.3.数:数出全部均等的结果数m和该事件出现的结果数n.4.算:代入公式P(A)=   .三、过关练习1.小颖有两件上衣，分别为红色和白色，有两条裤子，分别为黑色和白色，她随机拿出一件上衣和一条裤子穿上，恰好是白色上衣和白色裤子的概率是多少？    .总共有4种结果，每种结果出现的可能性相同，恰好白色上衣和白色裤子的概率为2.有5张看上去无差别的卡片，上面分别写着1，2，3，4，5，随机抽取3张，用抽到的三个数字作为边长，恰能构成三角形的概率是(　　)答案A 三张外观相同的卡片分别标有数字1，2，3，从中随机一次抽出两张，这两张卡片上的数字恰好都小于3的概率是(　　)答案A4.经过某十字路口的汽车，可能直行，也可能左转或者右转，如果这三种可能性大小相同，则经过这个十字路口的两辆汽车一辆左转、一辆右转的概率是(　　)答案C（2022盐城中考）某社区举行新冠疫情防控核酸检测大演练，卫生防疫部门在该社区设置了三个核酸检测点A、B、C，甲、乙两人任意选择一个检测点参加检测．求甲、乙两人不在同一检测点参加检测的概率．（用画树状图或列表的方法求解）解：画树状图如下：共有9种等可能的结果，其中甲、乙两人不在同一检测点参加检测的结果有6种，∴甲、乙两人不在同一检测点参加检测的概率为＝．四、课堂总结本节课你学到了什么？利树状图或表格，我们可以不重复、不遗漏地列出所有可能性相同的结果，从而比较方便地求出某些事件发生的概率.求概率的“四个步骤”：1.定:确定该试验的几个步骤、顺序、每一步可能产生的结果.2.画:列举或画树状图每一环节可能产生的结果.3.数:数出全部均等的结果数m和该事件出现的结果数n.4.算:代入公式P(A)= .  布置作业 教材第62页习题3.1第1、2题. 板书设计课题：3.1.1  用树状图法或表格求概率一、树状图二、列表法三、解决问题教学反思在教学时要反复强调：在借助于树状图或表格求事件发生的概率时,应注意到各种情况出现的等可能性．以免学生忽略这个条件错误使用树状图或表格求事件发生的概率.