

所属成套资源:【最新版】高中数学高三培优小题练【共96套】
【最新版】高中数学高三培优小题练第84练 用样本估计总体
展开
这是一份【最新版】高中数学高三培优小题练第84练 用样本估计总体,共8页。
考点一 用样本的数字特征估计总体
1.在某次测量中得到A的样本数据如下:42,43,46,52,42,50,若B样本数据恰好是A样本数据每个都减5后所得数据,则A,B两样本的下列数字特征对应相同的是( )
A.平均数 B.标准差
C.众数 D.中位数
答案 B
解析 由B样本数据恰好是A样本数据每个都减5后所得数据,可得平均数、众数、中位数分别是原来结果减去5,即与A样本不相同,标准差不变,故选B.
2.对某商店一个月内每天的顾客人数进行了统计,得到样本数据如下所示,则该样本的中位数、众数、极差分别是( )
样本:12,15,20,22,23,23,31,32,34,34,38,39,45,45,45,47,47,48,48,49,50,50,51,51,54,57,59,61,67,68
A.46,45,56 B.46,45,53
C.47,45,56 D.45,47,53
答案 A
解析 由题意可知共有30个数值,所以中位数为第15个数和第16个数的平均值,即eq \f(45+47,2)=46;众数是45;极差为68-12=56.
3.某地区某村前三年的经济收入分别为100,200,300万元,其统计数据的中位数为x,平均数为y.经过今年政府新农村建设后,该村经济收入在上年基础上翻番,则在这四年里收入的统计数据中,下列说法正确的是( )
A.中位数为x,平均数为1.5y
B.中位数为1.25x,平均数为y
C.中位数为1.25x,平均数为1.5y
D.中位数为1.5x,平均数为2y
答案 C
解析 依题意,前三年经济收入的中位数x=200,
平均数y=eq \f(100+200+300,3)=200,
第四年收入为600万元,
故这四年经济收入的中位数为eq \f(200+300,2)=250=1.25x,平均数为eq \f(100+200+300+600,4)=300=1.5y.
考点二 频率分布直方图
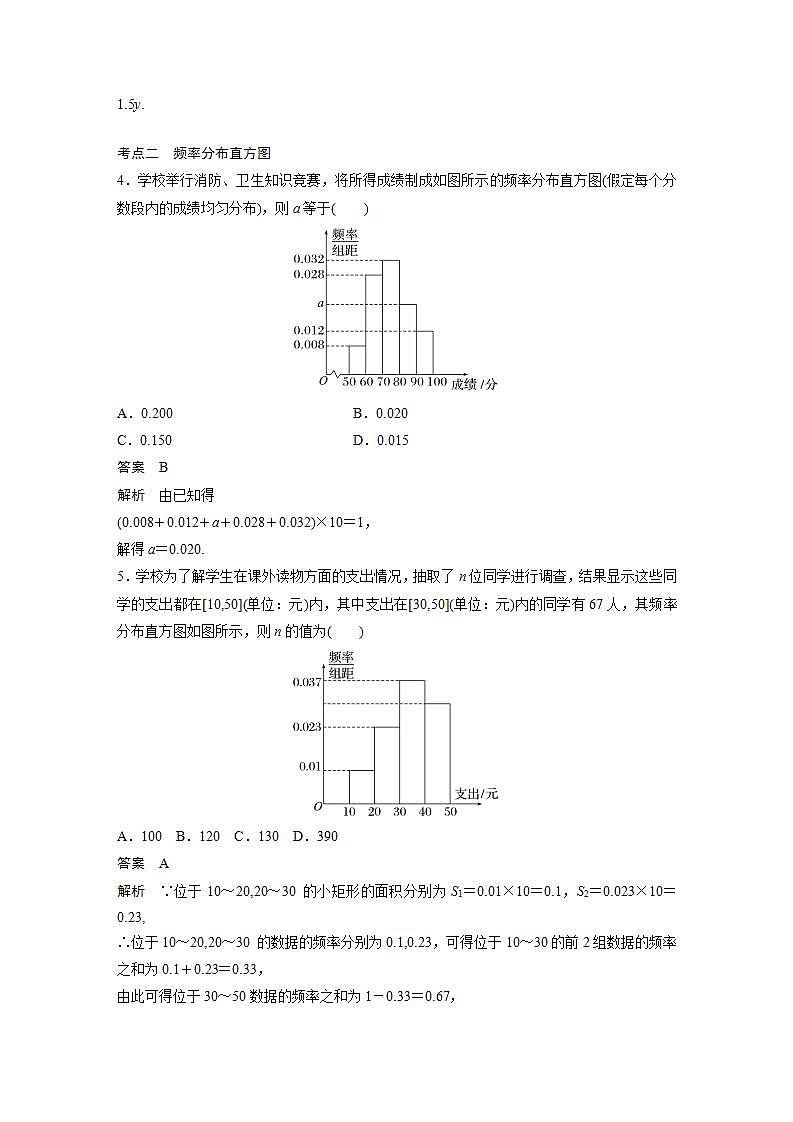
4.学校举行消防、卫生知识竞赛,将所得成绩制成如图所示的频率分布直方图(假定每个分数段内的成绩均匀分布),则a等于( )
A.0.200 B.0.020
C.0.150 D.0.015
答案 B
解析 由已知得
(0.008+0.012+a+0.028+0.032)×10=1,
解得a=0.020.
5.学校为了解学生在课外读物方面的支出情况,抽取了n位同学进行调查,结果显示这些同学的支出都在[10,50](单位:元)内,其中支出在[30,50](单位:元)内的同学有67人,其频率分布直方图如图所示,则n的值为( )
A.100 B.120 C.130 D.390
答案 A
解析 ∵位于10~20,20~30 的小矩形的面积分别为S1=0.01×10=0.1,S2=0.023×10=0.23,
∴位于10~20,20~30 的数据的频率分别为0.1,0.23,可得位于10~30的前2组数据的频率之和为0.1+0.23=0.33,
由此可得位于30~50数据的频率之和为1-0.33=0.67,
∵支出在[30,50]的同学有 67人,即位于30~50的频数为67,
根据频率计算公式,可得eq \f(67,n)=0.67,解得n=100.
6.(2022·大连模拟)供电部门对某社区1 000位居民2021年12月份人均用电情况进行统计后,按人均用电量分为[0,10),[10,20),[20,30),[30,40),[40,50]五组,整理得到如下的频率分布直方图,则下列说法错误的是( )
A.12月份人均用电量人数最多的一组有400人
B.12月份人均用电量不低于20度的有500人
C.12月份人均用电量为25度
D.在这1 000位居民中任选1位协助收费,选到的居民用电量在[30,40)内的概率为eq \f(1,10)
答案 C
解析 对于A,根据频率分布直方图知,人数最多的一组是[10,20),
有0.04×10×1 000=400(人),故选项A正确;
对于B,12月份用电量不低于20度的频率是(0.03+0.01+0.01)×10=0.5,
有1 000×0.5=500(人),故选项B正确;
对于C,12月份人均用电量为
(5×0.01+15×0.04+25×0.03+35×0.01+45×0.01)×10=22(度),故选项C错误;
对于D,用电量在[30,40)的有0.01×10×1 000=100(人),
所以1 000位居民中任选1位,选到的居民用电量在[30,40)内的概率为P=eq \f(100,1 000)=eq \f(1,10),故选项D正确.
7.200辆汽车通过某一段公路时的时速的频率分布直方图如图所示,则时速的众数、中位数的估计值分别为( )
A.62,62.5 B.65,62
C.65,62.5 D.62.5,62.5
答案 C
解析 ∵最高的矩形为第三个矩形,
∴时速的众数的估计值为65.前两个矩形的面积为(0.01+0.03)×10=0.4.
∵0.5-0.4=0.1,eq \f(0.1,0.4)×10=2.5,
∴中位数的估计值为60+2.5=62.5.
考点三 茎叶图、条形图、扇形图、折线图等统计图
8.已知甲、乙两名篮球运动员进行罚球训练,每人练习10组,每组罚球40个,每组命中个数的茎叶图如图所示,则下列结论错误的是( )
A.甲命中个数的极差是29
B.乙命中个数的众数是21
C.甲的命中率比乙高
D.甲命中个数的中位数是25
答案 D
解析 由茎叶图可知甲命中个数的极差为37-8=29,故A正确;易知乙命中个数的众数是21,故B正确;
甲的命中率为
eq \f(8+12+13+20+22+24+25+26+27+37,40×10)=0.535,
乙的命中率为
eq \f(9+11+13+14+18+19+20+21+21+23,40×10)=0.422 5,
所以甲的命中率比乙高,C正确;甲命中个数的中位数为eq \f(22+24,2)=23,D不正确.
9.若干年前,某教师刚退休的月退休金为6 000元,月退休金各种用途占比统计的条形图如图1,该教师退休后加强了体育锻炼,目前月退休金各种用途占比统计的折线图如图2.已知目前的月就医费比刚退休时少100元,则目前该教师的月退休金为( )
图1 图2
A.6 500元 B.7 000元
C.7 500元 D.8 000元
答案 D
解析 由条形图可知,刚退休时的月就医费为6 000×15%=900(元),则目前的月就医费为900-100=800(元),再由折线图可知,目前月就医费占退休金的10%,所以目前该教师的月退休金为eq \f(800,10%)=8 000(元).
10.(2022·洛阳模拟)在全国人民的共同努力下,特别是医护人员的奋力救治下,“新冠肺炎”疫情得到了有效控制.如图是国家卫健委给出的全国疫情通报,甲、乙两个省份从2月7日到2月13日一周的新增“新冠肺炎”确诊人数的折线图.
则下列关于甲、乙两省新增确诊人数的说法,不正确的是( )
A.甲省的平均数比乙省低
B.甲省的方差比乙省大
C.甲省的中位数是27
D.乙省的极差是12
答案 C
解析 对于A项,由折线图数据计算可得甲省的平均数比乙省低,故A项正确;
对于B项,由折线图可知,乙省数据的波动范围小于甲省数据的波动范围,
故乙省方差小于甲省的方差,故B项正确;
对于C项,由折线图数据可得甲省的数据从小到大排列为9,11,13,24,27,28,28,
故甲省的中位数为24,故C项错误;
对于D项,由折线图数据可得乙省的极差为29-17=12,故D项正确.
11.为了更好地支持“中小微企业”发展,某市决定对部分企业的税收进行适当减免.某机构调查了当地的中小微企业的年收入情况,根据所得的数据画出了样本频率分布直方图,下面有三个结论:
①样本数据落在区间eq \b\lc\[\rc\)(\a\vs4\al\c1(300,500))的频率为0.45;
②如果规定年收入在500万元以内的企业才能享受税收减免政策,那么估计当地有55%的中小微企业能享受到这一政策;
③样本的中位数为480万元,
其中正确结论的个数为( )
A.0 B.1 C.2 D.3
答案 D
解析 由频率分布直方图可得
eq \b\lc\(\rc\)(\a\vs4\al\c1(0.001+0.002+2a+0.001 5+0.000 5))×100
=1,
∴a=0.002 5.
①∵样本数据落在区间eq \b\lc\[\rc\)(\a\vs4\al\c1(300,500))的频率为eq \b\lc\(\rc\)(\a\vs4\al\c1(0.002+0.002 5))×100=0.45,∴①正确.
②∵年收入在500万元以内的频率为
(0.001+0.002+0.002 5)×100=0.55,
∴估计当地有55%的中小微企业能享受到税收减免政策,∴②正确.
③∵样本的中位数为400+eq \f(0.5-0.3,0.25)×100=480,∴③正确.
∴正确结论的个数为3.
12.(2022·云南师大附中模拟)袁隆平院士是中国杂交水稻事业的开创者,是当代神农.50多年来,他始终在农业科学的第一线辛勤耕耘,不懈探索,为人类运用科技手段战胜饥饿带来了绿色的希望和金色的收获.袁老的科研团队在发现“野败”后,将其带回实验,设计了试验田一、二.通过随机抽样法在两块试验田中分别抽取20株水稻,并统计每株水稻的稻穗数(单位:颗),得到如图所示的茎叶图,则下列说法错误的是( )
A.试验田二的中位数是246
B.试验田一的标准差小于试验田二的标准差
C.试验田一的平均数eq \x\t(x)1小于试验田二的平均数eq \x\t(x)2.
D.试验田一的众数是215
答案 B
解析 根据茎叶图知试验田二稻穗数的中位数是246,故A正确;
试验田一数据的离散程度较大,所以试验田一稻穗数的标准差大于试验田二稻穗数的标准差,故B错误;
试验田一的数据集中于区间(200,220),而试验田二的数据集中于区间(240,260),所以eq \x\t(x)1
相关试卷
这是一份【最新版】高中数学高三培优小题练第15练 函数小题综合练,共6页。
这是一份【最新版】高中数学高三培优小题练第14练 函数小题易错练,共6页。试卷主要包含了已知a>0,则化为等内容,欢迎下载使用。
这是一份【最新版】高中数学高三培优小题练第20练 导数小题易错练,共7页。试卷主要包含了函数f=x2的单调递减区间是,已知过点A作曲线C等内容,欢迎下载使用。










