
湘教版九年级上册第1章 反比例函数综合与测试单元测试巩固练习
展开湘教版初中数学九年级上册第一章《反比例函数》单元测试卷
考试范围:第一章;考试时间:120分钟;总分120分
学校:___________姓名:___________班级:___________考号:___________
第I卷(选择题)
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
1. 下列函数中,表示y是x的反比例函数的是( )
A. y=3x B. y=ax C. y=8x2 D. y=13x
2. 下面关系式,中x与y不成正比例(x、y均不为零).( )
A. x:y=3 B. 5x=6y C. 4x=y D. x=13y
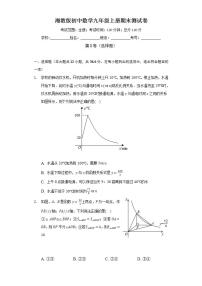
3. 如图,在平面直角坐标系xOy中,点A的坐标是(5,0),点B是函数y=6x(x>0)图象上的一个动点,过点B作BC⊥y轴交函数y=−2x(x<0)的图象于点C,点D在x轴上(D在A的左侧),且AD=BC,连接AB,CD.
有如下四个结论:
①四边形ABCD可能是菱形;
②四边形ABCD可能是正方形;
③四边形ABCD的周长是定值;
④四边形ABCD的面积是定值.
所有正确结论的序号是( )
A. ①② B. ③④ C. ①③ D. ①④
4. 如图,四边形OABC和四边形BDEF都是正方形,反比例函数y=kx在第一象限的图象经过点E,若两正方形的面积差为12,则k的值为( )
A. 12
B. 6
C. −12
D. 8
5. 如图,菱形ABCD的四个顶点均在坐标轴上,对角线AC、BD交于原点O,AE⊥BC于E点,交BD于M点,反比例函数y=33x(x>0)的图象经过线段DC的中点N,若BD=4,则ME的长为( )
A. ME=53 B. ME=43 C. ME=1 D. ME=23
6. 将一块含30°角的三角板ABC按如图所示摆放在平面直角坐标系中,直角顶点C在x轴上,AB // x轴.反比例函数y=kxx>0的图象恰好经过点A,且与直角边BC交于点D.若AB=63,BD=2 CD,则k的值为( )
A. 923 B. 63 C. 2033 D. 2743
7. 如图,在平面直角坐标系中,平行四边形OABC的边OA在y轴的正半轴上,反比例函数y=kx(x>0)的图象分别交AB于中点D,交OC于点E,且CE:OE=1:2,连接AE,DE,若S△ADE=2,则k的值为( )
A. 5 B. 367 C. 6 D. 647
8. 如图,反比例函数y=kx(k>0)与一次函数y=12x+b的图象相交于两点A(x1,y1),B(x2,y2),线段AB交y轴于C,当|x1−x2|=2且AC=2BC时,k、b的值分别为( )
A. k=12,b=2
B. k=49,b=1
C. k=13,b=13
D. k=49,b=13
9. 如图,在平面直角坐标系中,直线y=3x+3与x轴、y轴分别交于A、B两点,以AB为边在第二象限作正方形ABCD,将过点D的双曲线y=k1x(x<0)沿y轴对折,得到双曲线y=k2x(x>0),则k2的值是( )
A. 3 B. 4 C. 6 D. 8
10. 春季是传染病多发的季节,积极预防传染病是学校高度重视的一项工作,为此,某校对学生宿舍采取喷洒药物的措施进行消毒.在对某宿舍进行消毒的过程中,先经过5min的集中药物喷洒,再封闭宿舍10min,然后打开门窗进行通风.室内空气中含药量y(mg/m3)与药物在空气中的持续时间x(min)之间的函数关系,在打开门窗通风前分别满足两个一次函数,在通风后又成反比例,图像如图所示.下列选项中,错误的是( )
A. 经过5min的集中药物喷洒,室内空气中的含药量最高达到10mg/m3
B. 室内空气中的含药量不低于8mg/m3的持续时间达到了11min
C. 若室内空气中的含药量不低于5mg/m3且持续时间不低于35min,才能有效杀灭某种传染病毒,则此次消毒完全有效
D. 当室内空气中的含药量低于2mg/m3时,对人体才是安全的,所以从室内空气中的含药量达到2mg/m3开始,需经过59min后,学生才能进入室内
11. 教室里的饮水机接通电源就进入自动程序,开机加热时每分钟水温上升10°C,加热到100°C,停止加热,水温开始下降,此时水温(°C)与开机后用时(min)成反比例函数关系.直至水温降至30°C,饮水机关机,饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30°C时,接通电源后,水温y(°C)和时间x(min)的关系如图所示,为了在上午第一节下课时(8:45)能喝到不超过50°C的水,则接通电源的时间可以是当天上午的( )
A. 7:20 B. 7:30 C. 7:45 D. 7:50
12. 如图,在直角坐标系中,矩形OABC的顶点A、B在双曲线y=kx(x>0)上,BC与x轴交于点D.若点A的坐标为(2,4),则点D的坐标为( )
A. (223,0)
B. (152,0)
C. (689,0)
D. (485,0)
第II卷(非选择题)
二、填空题(本大题共4小题,共12.0分)
13. 函数y=(m+1)xm2−2m−4是y关于x的反比例函数,则m=______.
14. 若是反比例函数,则a的取值为______.
15. 如图,反比例函数y=3x与一次函数y=x−2在第三象限交于点A,点B的坐标为(−3,0),点P是y轴左侧的一点,若以A,O,B,P为顶点的四边形为平行四边形,则点P的坐标为______.
16. 如图,直线y=x+n与y轴的正半轴交于点A,与双曲线y=6x交于点P,Q(点Q在第一象限内),过点Q作QB⊥x轴于点B,若S△AOP−S梯形AOBQ=6,则n的值为______.
三、解答题(本大题共9小题,共72.0分。解答应写出文字说明,证明过程或演算步骤)
17. (本小题8.0分)
为加强生态文明建设,某市环保局对一企业排污情况进行检测,结果显示:所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1.0mg/L.环保局要求该企业立即整改,在15天内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度y(mg/L)与时间x(天)的变化规律如图所示,其中线段AC表示前3天的变化规律,第3天时硫化物的浓度降为4.5mg/L.从第3天起,所排污水中硫化物的浓度y与时间x满足下面表格中的关系:
时间x(天)
3
5
6
9
……
硫化物的浓度y(mg/L)
4.5
2.7
2.25
1.5
……
(1)在整改过程中,当0≤x<3时,硫化物的浓度y与时间x的函数表达式;
(2)在整改过程中,当x≥3时,硫化物的浓度y与时间x的函数表达式;
(3)该企业所排污水中硫化物的浓度能否在15天以内不超过最高允许的1.0mg/L?为什么?
18. (本小题8.0分)
小涂在课余时间找到了几副度数不同的老花镜,让镜片正对着太阳光,并上下移动镜片,直到地上的光斑最小(可以认为是焦点),此时他测了镜片与光斑的距离(可以当做焦距),得到如下数据:
老花镜的度数D/度
100
120
200
250
300
焦距f/m
1
0.8
0.5
0.4
0.3
(1)老花镜镜片是______(凸的、凹的、平的),度数越高镜片的中心______(越薄、越厚、没有变化);
(2)观察表中的数据,可以找出老花镜的度数D与镜片焦距f的关系,用关系式表示为:______;
(3)如果按上述方法测得一副老花镜的焦距为0.7m,可求出这幅老花镜的度数为______.
19. (本小题8.0分)
某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y (℃)与时间x(h)之间的函数关系,其中线段AB、BC表示恒温系统开启阶段,双曲线的一部分CD表示恒温系统关闭阶段.
请根据图中信息解答下列问题:
(1)求这天的温度y与时间x(0≤x≤24)的函数关系式;
(2)求恒温系统设定的恒定温度;
(3)若大棚内的温度低于10℃时,蔬菜会受到伤害.问这天内,恒温系统最多可以关闭多少小时,才能使蔬菜避免受到伤害?
20. (本小题8.0分)
已知函数y=y1+y2,y1与x成正比例,y2与x成反比例.当x=1时,y=2;当x=2时,y=−2,求当x=−1时y的值.
21. (本小题8.0分)
如图,直线y=x−1与反比例函数y=kx的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(−1,m).
(1)求反比例函数的解析式;
(2)若点P(n,−1)是反比例函数图象上一点,过点P作PE⊥ x轴于点E,延长EP交直线AB于点F,求△ CEF的面积.
22. (本小题8.0分)
如图,已知一次函数y1=kx+b的图象与x轴相交于点A,与反比例函数y2=cx相交于B(−1,5),C(52,d)两点.
(1)利用图中条件,求反比例和一次函数的解析式;
(2)连接OB,OC,求△BOC的面积.
(3)根据图像直接写出不等式kx+b>cx>0的解集.
23. (本小题8.0分)
如图,在平面直角坐标系xOy中,点A(a,−72)在直线y=−32x−12上,AB // y轴,且点B的纵坐标为1,双曲线y=mx经过点B.
(1)求a的值及双曲线y=mx的解析式;
(2)经过点B的直线与双曲线y=mx的另一个交点为点C,且△ABC的面积为274.
①求直线BC的解析式;
②过点B作BD // x轴交直线y=−32x−12于点D,点P是直线BC上的一个动点.若将△BDP以它的一边为对称轴进行翻折,翻折前后的两个三角形所组成的四边形为正方形,直接写出所有满足条件的点P的坐标.
24. (本小题8.0分)
如图,在平面直角坐标系中,四边形ABCD为正方形,已知点A(−6,0)、D(−7,3),点B、C在第二象限内.
(1)点B的坐标____;
(2)将正方形ABCD以每秒2个单位的速度沿x轴向右平移t秒,若存在某一时刻t,使在第一象限内点B、D两点的对应点Bˈ、Dˈ正好落在某反比例函数的图象上,请求出此时t的值以及这个反比例函数的解析式;
(3)在(2)的情况下,问是否存在y轴上的点P和反比例函数图象上的点Q,使得以P、Q、Bˈ、Dˈ四个点为顶点的四边形是平行四边形?若存在,请直接写出符合题意的点P、Q的坐标;若不存在,请说明理由.
25. (本小题8.0分)
新冠肺炎疫情发生后,社会各界积极行动,以各种方式倾情支援湖北疫区,某车队需要将一批生活物资运送至湖北疫区.已知该车队计划每天运送的货物吨数y(吨)与运输时间x(天)之间满足如图所示的反比例函数关系.
(1)求该车队计划每天运送的货物吨数y(吨)与运输时间x(天)之间的函数关系式;(不需要写出自变量x的取值范围)
(2)根据计划,要想在5天之内完成该运送任务,则该车队每天至少要运送多少吨物资?
(3)为保证该批生活物资的尽快到位,该车队实际每天运送的货物吨数比原计划多了25%,最终提前了1天完成任务,求实际完成运送任务的天数.
答案和解析
1.【答案】D
【解析】
【分析】
本题考查的是反比例函数的定义,解题关键是掌握反比例函数的定义:形如y=kx(k为常数,k≠0)的函数称为反比例函数.解题时,根据反比例函数的定义对各选项进行逐一分析即可得出答案.
【解答】
解:A.y=3x不符合反比例函数的定义,故本选项不符合题意;
B.y=ax中的a可能为0,因此不符合反比例函数的定义,故本选项不符合题意;
C.y=8x2,不符合反比例函数的定义,故本选项不符合题意.
D.y=13x符合反比例函数的定义,是反比例函数,故本选项符合题意.
故选D.
2.【答案】C
【解析】
【分析】
本题考查正比例和反比例的意义,判断x与y是否成正比例,就看这两种量是否是对应的比值一定,如果是比值一定,就成正比例,如果不是比值一定(或比值不一定),就不成正比例.据此进行逐项分析再选择.
【解答】
解:A.因为xy=3 ,则比值一定,所以x与y成正比例;
B. 因为5x=6y,则有xy=65 (一定),是比值一定,所以x与y成正比例;
C. 因为4x=y ,则有xy=4(一定),是乘积一定,所以x与y成反比例;
D. 因为x=13y ,则有xy=13(一定),是比值一定,所以x与y成正比例. 故选C.
3.【答案】D
【解析】解:①∵BC⊥y轴,
∴AD//BC,
又∵AD=BC,
∴四边形ABCD是平行四边形,
设点B(a,6a),则C(−a3,6a),
∴BC=a−(−a3)=43a,AB=(5−a)2+(6a)2,
当a=5时,BC=203,AB=65,
此时,AB
∴四边形ABCD可能是菱形,故①正确,符合题意;
②由①得,当x=5时,BC=203,AB=65,
∴BC≠AB,
∴四边形ABCD不为正方形,故②错误,不符合题意;
③由①得,当点B的横坐标为5时,BC=203,AB=65,
∴C四边形ABCD=2×(BC+AB)=2×(203+65)=23615,
当点B的横坐标为1时,B(1,6),C(−13,6),
∴BC=43,AB=(5−1)2+62=213,
∴C四边形ABCD=2(BC+AB)=2(43+213)=83+413≠23615,
∴四边形ABCD的周长不为定值,故③错误,不符合题意;
④如图,过点C作CE⊥x轴于点E,过点B作BF⊥x轴于点F,则四边形EFBC为矩形,
∵BC//AD,
∴S四边形ABCD=S四边形EFBC=|−2|+|6|=8,
∴四边形ABCD的面积为定值,故④正确,符合题意;
故选:D.
①由BC⊥y轴得到AD//BC,结合AD=BC,得到四边形ABCD是平行四边形,设点B(a,6a),则C(−a3,6a),得到BC的长,再表示AB的长,利用菱形的性质列出方程求得a的值,即可判断结论;
②当x=5时,求得点B的坐标,然后判断四边形ABCD是否为正方形;
③任取两个点B的坐标,求得AB和BC的长,然后判断四边形ABCD的周长是否为定值;
④过点C作CE⊥x轴于点E,过点B作BF⊥x轴于点F,将四边形ABCD的面积转化为四边形EFBC的面积,进而利用反比例系数k的几何意义判断四边形ABCD的面积是否为定值.
本题考查了反比例函数图象上点的坐标特征,平行四边形的判定与性质,菱形的性质,正方形的性质,解题的关键是熟知反比例函数图象上点的坐标特征.
4.【答案】A
【解析】
【分析】
本题考查了反比例函数比例系数k的几何意义:在反比例函数y=kx图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.也考查了正方形的性质.
设正方形OABC、BDEF的边长分别为a和b,则可表示出D(a,a−b),F(a+b,a),根据反比例函数图象上点的坐标特征得到E(a+b,ka+b),由于点E与点D的纵坐标相同,所以ka+b=a−b,则a2−b2=k,然后利用正方形的面积公式易得k=12,即可解答.
【解答】
解:设正方形OABC、BDEF的边长分别为a和b,则D(a,a−b),F(a+b,a),
所以E(a+b,ka+b),
所以ka+b=a−b,
∴(a+b)(a−b)=k,
∴a2−b2=k,
∵两正方形的面积差为12,
∴k=12.
故选:A.
5.【答案】D
【解析】
【分析】
此题主要考查了反比例函数和菱形的综合运用,关键是掌握菱形的性质:菱形对角线互相垂直平分,且平分每一组对角,反比例函数图象上的点横纵坐标之积=k.
过N作y轴和x轴的垂线NG,NH,证明四边形NGOH是矩形,设N(b,a),根据反比例函数图象上点的坐标特点可得ab=33,进而可计算出CO长,根据三角函数可得∠CDO=30°,再根据菱形的性质可得∠ABC=∠ADC=2∠CDO=60°,∠ACD=60°,进而即可证得△ABC是等边三角形,得出AE=OB=2,由∠BAE=30°=∠ABO,得出AM=BM,则EM=OM,从而得到3EM=OB=2,进而可得EM的长.
【解答】
解:过N作y轴和x轴的垂线NG,NH,
设N(b,a),
∵反比例函数y=33x(x>0)的图象经过点N,
∴ab=33,
∵四边形ABCD是菱形,
∴BD⊥AC,DO=12BD=2,
∵NH⊥x轴,NG⊥y轴,
∴四边形NGOH是矩形,
∴NG//x轴,NH//y轴,
∵N为CD的中点,
∴DO⋅CO=2a⋅2b=4ab=433,
∴CO=233,
∴tan∠CDO=OCDO=33.
∴∠CDO=30°,
∴∠DCO=60°,
∵四边形ABCD是菱形,
∴∠ADC=∠ABC=2∠CDO=60°,∠ACB=∠DCO=60°,
∴△ABC是等边三角形,
∵AE⊥BC,BO⊥AC,
∴AE=BO=2,∠BAE=30°=∠ABO,
∴AM=BM,
∴OM=EM,
∵∠MBE=30°,
∴BM=2EM=2OM,
∴3EM=OB=2,
∴ME=23.
6.【答案】D
【解析】
【分析】
本题考查了反比例函数图象上点的坐标特征,平行线的性质,含30°角直角三角形的性质.
过点A作AE⊥x轴,垂足为E,过点D作DF⊥x轴,垂足为F,求得AE,CE,CF,DF,设OE=x,求得A(x,92),D(x+33,32),然后根据反比例函数图象上点的坐标特征得出92x=(x+33)×32,解出x的值,求出A(332,92),再计算k的值.
【解答】
解:如图,过点A作AE⊥x轴,垂足为E,过点D作DF⊥x轴,垂足为F,
在Rt△ABC中,∠B=30°,AB//x轴,AB=63,BD=2CD,
∴AC=33,BC=9,∠DCF=30°,∠EAC=30°,
∴EC=12AC=332,DC=3,
DF=12DC=32,
∴CF=332,AE=92,
设OE=x,则OF=OE+EC+CF=x+332+332=x+33,
∴A(x,92),D(x+33,32),
又∵点A、D都在反比例函数的图象上,
∴92x=(x+33)×32,
解得,x=332,
∴A(332,92),
∴k=332×92=2743.
7.【答案】D
【解析】解:如图,连接AC,BE.
∵AD=DB,
∴S△ADE=S△BDE=2,
∵四边形AOCB是平行四边形,
∴S△AOC=12S平行四边形AOBC=S△AEB=4,
∵OE=2EC,
∴S△AOE=23S△AOC=83,
设A(0,b),C(a,t),则B(a,b+t),D(12a,2b+t2),E(23a,23t),
∵D,E在反比例函数的图象上,
∴12⋅a⋅2b+t2=49at,
整理得t=187b,
∴E(23a,127b),
∴12×b×23a=83,
∴ab=8,
∴k=23a×127b=647,
故选:D.
如图,连接AC,BE.首先确定S△AOE=23S△AOC=83,设A(0,b),C(a,t),则B(a,b+t),D(12a,2b+t2),E(23a,23t),因为D,E在反比例函数的图象上,所以12⋅a⋅2b+t2=49at,整理得t=187b,推出E(23a,127b),利用面积关系求出ab的值,可得结论.
本题考查反比例函数的性质,平行四边形的性质,三角形的面积等知识,解题的关键是学会利用参数解决问题,属于中考选择题中的压轴题.
8.【答案】D
【解析】
【分析】
此题综合考查了反比例函数、一次函数的性质,注意通过解方程求出k、b的值.此题难度稍大,综合性比较强,注意对各个知识点的灵活应用.
首先由AC=2BC,可得出A点的横坐标的绝对值是B点横坐标绝对值的两倍.再由|x1−x2|=2,可求出A点与B点的横坐标,然后根据点A、点B既在一次函数y=12x+b的图象上,又在反比例函数y=kx(k>0)的图象上,可求出k、b的值.
【解答】
解:∵AC=2BC,点C在y轴上,
∴A点的横坐标的绝对值是B点横坐标绝对值的两倍.
∵点A、点B都在一次函数y=12x+b的图象上,
∴可设B(m,12m+b),则A(−2m,−m+b).
∵|x1−x2|=2,
∴m−(−2m)=2,
∴m=23;
又∵点A、点B都在反比例函数y=kx(k>0)的图象上,
∴23(13+b)=(-43)(-23+b),
∴b=13,
∴k=23(13+13)=49.
故选D.
9.【答案】B
【解析】解:如图,过点D作DE⊥x轴于点E,则∠AED=∠AOB=90°
在y=3x+3中,令x=0,得y=3,∴B(0,3),
令y=0,得0=3x+3,解得x=−1,∴A(−1,0),
∴OA=1,OB=3,
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°
∴∠BAO+∠ABO=∠BAO+∠DAE=90°
∴∠ABO=∠DAE
在△ABO和△DAE中
∠ABO=∠DAE∠AOB=∠AEDAB=AD
∴△ABO≌△DAE(AAS)
∴DE=OA=1,AE=OB=3
∴OE=OA+AE=1+3=4
∴D(−4,1)
把D(−4,1)代入y=k1x中,得1=k1−4
∴k1=−4
∴y=−4x(x<0);
∵双曲线y=k1x(x<0)沿y轴对折,得到双曲线y=k2x(x>0),
即双曲线y=k1x(x<0)与双曲线y=k2x(x>0)关于y轴对称,
∴k2=4.
故选:B.
先求出点A、B的坐标,根据正方形性质证明△ABO≌△DAE(AAS),即可求得点D坐标,进而可求得k1的值,再利用双曲线y=k1x(x<0)与双曲线y=k2x(x>0)关于y轴对称,即可求得k2.
本题考查了一次函数图象与坐标轴交点,正方形性质,全等三角形判定和性质,反比例函数图象和性质,翻折变换的性质,关于y轴对称的反比例函数解析式的关系等知识点,是一道综合性较强,涉及知识点较多的代数几何综合题,解题关键是利用正方形性质构造全等三角形.
10.【答案】C
【解析】
【分析】
本题考查反比例函数的应用、一次函数的应用等知识,解题的关键是读懂图象信息,属于中考常考题型.利用图中信息一一判断即可.
【解答】
解:由图象可得当x≤5时,函数关系式为y=2x,当x>15时,函数关系式为y=120x ,
A.正确.不符合题意.
B.对一次函数y=2x,当x=4时,y=8,∴室内空气中的含药量不低于8mg/m3的持续时间达到了15−4=11min,正确,不符合题意;
C.对一次函数y=2x,当y=5时,x=2.5,对反比例函数y=120x,当y=5时,x=24,24−2.5=21.5<35,故本选项错误,符合题意;
D.当x≤5时,函数关系式为y=2x,y=2时,x=1;
当x>15时,函数关系式为y=120x ,y=2时,x=60;60−1=59,
故当室内空气中的含药量低于2mg/m3时,对人体才是安全的,
所以从室内空气中的含药量达到2mg/m3开始,需经过59min后,学生才能进入室内,正确.不符合题意,
故选C.
11.【答案】A
【解析】
【分析】
本题主要考查了一次函数及反比例函数的应用题,同学们在解答时要读懂题意,才不易出错 解决分段函数问题,要根据自变量的取值范围选择相应的函数表达式.
第1步:求出两个函数的解析式;
第2步:求出饮水机完成一个循环周期所需要的时间;
第3步:求出每一个循环周期内,水温不超过50℃的时间段;
第4步:结合4个选择项,逐一进行分析计算,得出结论.
【解答】
解:开机加热时水温每分钟上升10°C,
∴水温从30°C升到100°C需要7min.
当0≤x≤7时,设y=k1x+b,将(0,30),(7,100)代入y=k1x+b,得k1=10,b=30,
∴当0≤x≤7时,y=10x+30;
设水温第一次降至30°C时的时间为amin,当7
∴703min为一个循环周期.
当在上午7:20接通电源时,7:20∼8:45共85min,85−703×3=15(min),y=70015=1403<50,符合题意.同理可验证B,C,D选项均不符合题意.
故选A.
12.【答案】B
【解析】
【分析】
本题考查的是一次函数图象上点的坐标特点,矩形的性质,待定系数法求一次函数的解析式和反比例函数的解析式,由矩形OABC的顶点A、B在双曲线y=kx( x>0)上,BC与x轴交于点D.若点A的坐标为(2,4),利用待定系数法即可求得反比例函数与直线OA的解析式,又由OA⊥AB,可得直线AB的系数为−12,继而可求得直线AB的解析式,将直线AB与反比例函数联立,即可求得点B的坐标,设直线BD的解析式为y=2x+c,代入求出解析式,再求出直线和x轴的交点坐标即可.
【解答】
解:∵矩形OABC的顶点A、B在双曲线y=1k( x>0)上,点A的坐标为(2,4),
∴4=k2,
解得:k=8,
∴双曲线的解析式为:y=8x,直线OA的解析式为:y=2x,
∵OA⊥AB,
∴设直线AB的解析式为:y=−12x+b,
∴4=−12×2+b,
解得:b=5,
∴直线AB的解析式为:y=−12x+5,
将直线AB与反比例函数联立得出:y=8xy=−12x+5,
解得:x=2y=4或x=8y=1.
∴点B(8,1),
∵四边形AOCB是矩形,
∴AO//BD,
∵直线OA的解析式为y=2x,
∴设直线BD的解析式为y=2x+c,
把B的坐标代入得:1=16+c,
解得c=−15,
即y=2x−15,
当y=0时,x=152,
即D的坐标为(152,0).
故选B.
13.【答案】3
【解析】
【分析】
本题考查的反比例函数的定义有关知识,根据题意可得:m+1≠0,m2−2m−4=−1即可解答.
【解答】
解:由题意可得m+1≠0,m2−2m−4=−1
解得:m=3.
故答案为3.
14.【答案】1
【解析】
【分析】
本题考查了反比例函数的定义,重点是知道y=kx−1(k≠0)是反比例函数.根据反比例函数的定义直接解答即可.
【解答】
解:∵若y=a+1xa2−2是反比例函数,
∴a2−2=−1,
解得,a2=1,
a=±1,
∵a+1≠0,
∴a≠−1,
所以a=1.
故答案为1.
15.【答案】(−4,−3),(−2,3)
【解析】解:由题意得y=x−2y=3x,解得x=3y=1或x=−1y=−3,
∵反比例函数y=3x与一次函数y=x−2在第三象限交于点A,
∴A(−1,−3).
当以AB为对角线时,AB的中点坐标M为(−2,−1.5),
∵平行四边形的对角线互相平分,
∴M为OP中点,
设P点坐标为(x,y),
则x+02=−2,y+02=−1.5,
解得x=−4,y=−3,
∴P(−4,−3).
当OB为对角线时,
由O、B坐标可求得OB的中点坐标M(−32,0),设P点坐标为(x,y),
由平行四边形的性质可知M为AP的中点,
结合中点坐标公式可得x−12=−32,y−32=0,解得x=−2,y=3,
∴P(−2,3);
当以OA为对角线时,
由O、A坐标可求得OA的中点坐标M(−12,−32),设P点坐标为(x,y),
由平行四边形的性质可知M为BP中点,
结合中点坐标公式可得x−32=−12,y+02=−32,解得x=2,y=−3,
∴P(2,−3)(舍去).
综上所述,P点的坐标为(−4,−3),(−2,3).
故答案为:(−4,−3),(−2,3).
联立直线和反比例函数解析式可求出A点的坐标,再分以AB为对角线、以OA为对角线和以OB为对角线三种情况,利用平行四边形的性质可分别求得满足条件的P点的坐标.
本题考查的是反比例函数与一次函数的交点问题,熟知反比例函数图象上点的坐标特点、平行四边形的判定与性质及中点坐标公式是解答此题的关键.
16.【答案】32
【解析】解:设:点P、Q的坐标分别为(x1,y1)、(x2、y2),则x2y2=6,
直线y=x+n与y轴的正半轴交于点A,则OA=n,
联立直线与反比例函数表达式并整理得:x2+nx−6=0,
则x1+x2=−n,
S△AOP−S梯形AOBQ=6,
即:12×OA×x1+(AO+y2)x2=6,
即:AO(x1+x2)+x2y2=−12,
即−n2=−18,
解得:n=32(舍去负值),
故答案为:32.
联立直线与反比例函数表达式并整理得:x2+nx−6=0,则x1+x2=−n,由S△AOP−S梯形AOBQ=6得:AO(x1+x2)+x2y2=−12,即可求解.
本题考查的是反比例函数与一次函数的交点问题,要熟悉图象上的点与图象的关系,本题解题的难点在于利用韦达定理处理复杂数据.
17.【答案】解:(1)设线段AC的函数表达式为:y=kx+b,
∴b=123k+b=4.5,
∴b=12k=−2.5,
∴线段AC的函数表达式为:y=−2.5x+12(0≤x<3);
(2)∵3×4.5=5×2..7=...=13.5,
∴y是x的反比例函数,
∴y=13.5x(x≥3);
(3)当x=15时,y=13.515=0.9,
∵13.5>0,
∴y随x的增大而减小,
∴该企业所排污水中硫化物的浓度可以在15天以内不超过最高允许的1.0mg/L.
【解析】(1)设AC的函数关系式为:y=kx+b,将A和C代入,从而求得k,b,进而求得的结果;
(2)可推出x⋅y=13.5为定值,所以当x≥3时,y是x的反比例函数,进而求得结果;
(3)将x=15代入反比例函数关系式,从而求得y的值,进而根据反比例函数图象性质,从而得出结论.
本题考查了求一次函数关系式,反比例函数及其图象的性质等知识,解决问题的关键是熟练掌握反比例函数及其图象性质.
18.【答案】凸的 越厚 f=100D 143度
【解析】解:(1)老花镜镜片是凸的,度数越高镜片的中心越厚,
故答案为:凸的;越厚;
(2)根据表中数据可得:100×1=100,120×0.8=96,200×0.5=100,250×0.4=100,300×0.3=90,
则老花镜的度数D与镜片焦距f的关系可近似的看作f=100D,
故答案为:f=100D;
(3)当f=0.7m时,0.7=100D,
解得D≈143,
即这幅老花镜的度数是143度.
故答案为:143度.
(1)根据题意及常识可求解;
(2)利用表格中的数据可求解D与f的关系式;
(3)将f值代入计算可求解.
本题主要考查反比例函数的应用,根据数据找函数关系是解题的关键.
19.【答案】解:(1)设线段AB所在直线的解析式为y=k1x+b(k1≠0),
∵线段AB过点(0,10),(2,14),
代入得b=102k1+b=14,
解得k1=2b=10,
∴AB解析式为:y=2x+10(0≤x<5);
∵B在线段AB上,当x=5时,y=20,
∴点B的坐标为(5,20),
∴线段BC所在直线的解析式为:y=20(5≤x<10);
设双曲线CD的解析式为:y=k2x(k2≠0),
∵C(10,20),
∴k2=200,
∴双曲线CD解析式为:y=200x(10≤x≤24),
∴y关于x的函数解析式为:
y=2x+10(0≤x<5)20(5≤x<10)200x(10≤x≤24)
(2)由(1)恒温系统设定恒温为20℃;
(3)把y=10代入y=200x中,解得x=20,
∴20−10=10,
答:恒温系统最多关闭10小时,蔬菜才能避免受到伤害.
【解析】本题为实际应用背景的函数综合题,考查求一次函数、反比例函数和常函数关系式.解答时应注意临界点的应用.
(1)应用待定系数法分段求函数解析式;
(2)观察图象可得;
(3)代入临界值y=10即可.
20.【答案】解:设y1=k1x,y2=k2x,
则y=y1+y2=k1x+k2x,
把x=1时,y=2;x=2时,y=−2分别代入y=k1x+k2x中,
得:k1+k2=22k1+k22=−2
解得:k1=−2k2=4
∴函数关系式为y=−2x+4x,
当x=−1时,y=−2×(−1)+4−1=−2.
【解析】本题主要考查待定系数法求函数关系式以及求函数值,理解题中几个量之间的关系是解决问题的关键.先分别设出y1与x、y2与x的关系式,然后用已知xy的值代入关系式,用待定系数法求出k1、k2的值,从而得到y与x的关系式,最后把x=−1代入关系式求出y值即可.
21.【答案】解:(1)将点A的坐标代入y=x−1,可得:m=−1−1=−2,
将点A(−1,−2)代入反比例函数y=kx,可得:k=−1×(−2)=2,
故反比例函数解析式为:y=2x.
(2)将点P的纵坐标y=−1,代入反比例函数关系式可得:x=−2,
将点F的横坐标x=−2代入直线解析式可得:y=−3,
故可得EF=3,CE=OE+OC=2+1=3,
故可得S△CEF=12CE×EF=92.
【解析】本题考查了一次函数与反比例函数的交点问题,解答本题的关键是确定点A的坐标,要求同学们能结合图象及直角坐标系,将点的坐标转化为线段的长度.
(1)将点A的坐标代入直线解析式求出m的值,再将点A的坐标代入反比例函数解析式可求出k的值,继而得出反比例函数关系式;
(2)将点P的纵坐标代入反比例函数解析式可求出点P的横坐标,将点P的横坐标和点F的横坐标相等,将点F的横坐标代入直线解析式可求出点F的纵坐标,将点的坐标转换为线段的长度后,即可计算△CEF的面积.
22.【答案】解:(1)将B(−1,5)代入y2=cx得,c−1=5,
解得c=−5,
所以,反比例函数解析式为y=−5x,
将点C(52,d)代入y=−5x得d=−552=−2,
所以,点C的坐标为(52,−2),
将点B(−1,5),C(52,−2)代入一次函数y1=kx+b得,
−k+b=552k+b=−2,
解得k=−2b=3,
所以,一次函数y1=−2x+3;
(2)令y=0,则−2x+3=0,
解得x=32,
所以,点A的坐标为(32,0),
所以,OA=32,
S△BOC=S△AOB+S△AOC,
=12×32×5+12×32×2,
=214;
(3)x<−1.
∵B(−1,5),
∴由图象可得:不等式kx+b>cx>0的解集是x<−1,
故答案为x<−1.
【解析】本题考查了反比例函数与一次函数的交点,待定系数法求一次函数解析式,三角形的面积,利用点B的坐标先求出反比例函数解析式是解题的关键.
(1)将点B的坐标代入反比例函数解析式求出c,从而得解,再将点C的坐标代入反比例函数解析式求出d,从而得到点C的坐标,然后利用待定系数法求一次函数解析式求解;
(2)根据一次函数解析式求出点A的坐标,再根据S△BOC=S△AOB+S△AOC列式计算即可得解;
(3)根据点B的坐标结合图象即可得到答案.
23.【答案】解:(1)∵点A(a,−72)在直线y=−32x−12上,
∴−32a−12=72,解得a=2,
则A(2,−72),
∵AB//y轴,且点B的纵坐标为1,
∴点B的坐标为(2,1).
∵双曲线y=mx经过点B(2,1),
∴m=2×1=2,
∴反比例函数的解析式为y=2x;
(2)①设C(t,2t),
∵A(2,−72),B(2,1),
∴12×(2−t)×(1+72)=274,
解得t=−1,
∴点C的坐标为(−1,−2),
设直线BC的解析式为y=kx+b,
把B(2,1),C(−1,−2)代入得2k+b=1−k+b=−2,
解得k=1b=−1,
∴直线BC的解析式为y=x−1;
②当y=1时,−32x−12=1,解得x=−1,则D(−1,1),
∵直线BCy=x−1为直线y=x向下平移1个单位得到,
∴直线BC与x轴的夹角为45°,
而BD//x轴,
∴∠DBC=45°,
当△PBD为等腰直角三角形时,以它的一边为对称轴进行翻折,翻折前后的两个三角形所组成的四边形为正方形,
若∠BPD=90°,则点P在BD的垂直平分线上,P点的横坐标为12,当x=12时,y=x−1=−12,此时P(12,−12),
若∠BDP=90°,则PD//y轴,P点的横坐标为−1,当x=−1时,y=x−1=−2,此时P(−1,−2),
综上所述,满足条件的P点坐标为(−1,−2)或(12,−12).
【解析】本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.也考查了待定系数法求函数解析式和正方形的判定方法.
(1)根据一次函数图象上点的坐标特征可得到−32a−12=72,解得a=2,则A(2,−72),再确定点B的坐标为(2,1),然后把B点坐标代入y=mx中求出m的值即可得到反比例函数的解析式;
(2)①设C(t,2t),根据三角形面积公式得到12×(2−t)×(1+72)=274,解得t=−1,则点C的坐标为(−1,−2),再利用待定系数法求直线BC的解析式;
②先确定D(−1,1),根据直线BC解析式的特征可得直线BC与x轴的夹角为45°,而BD//x轴,于是得到∠DBC=45°,根据正方形的判定方法,只有△PBD为等腰直角三角形时,以它的一边为对称轴进行翻折,翻折前后的两个三角形所组成的四边形为正方形,分类讨论:若∠BPD=90°,则点P在BD的垂直平分线上,易得此时P(12,−12);若∠BDP=90°,利用PD//y轴,易得此时P(−1,−2).
24.【答案】解:(1)(−3,1);
(2)由(1)知,B(−3,1),
∵D(−7,3)
∴运动t秒时,点D′(−7+2t,3)、B′(−3+2t,1),
设反比例函数解析式为y=kx,
∵点B′,D′在反比例函数图象上,
∴k=(−7+2t)×3=(−3+2t)×1,
∴t=92,k=6,
∴反比例函数解析式为y=6x;
(3)存在,理由:
由(2)知,点D′(−7+2t,3)、B′(−3+2t,1),t=92,
∴D′(2,3)、B′(6,1),
由(2)知,反比例函数解析式为y=6x,
设点Q(m,6m),点P(0,s),
以P、Q、B′、D′四个点为顶点的四边形是平行四边形,
∴①当PQ与B′D′是对角线时,
∴12(0+m)=12(2+6),12(s+6m)=12(3+1),
∴m=8,s=134,
∴Q(8,34),P(0,134),
②当PB′与QD′是对角线时,
∴12(0+6)=12(2+m),12(s+1)=12(6m+3),
∴m=4,s=72,
∴Q(4,32),P(0,72).
③当PD′与QB′是对角线时,
∴12(0+2)=12(m+6),12(s+3)=12(6m+1),
∴m=−4,s=−72,
∴Q(−4,−32),P(0,−72),
综上:Q(8,34),P(0,134)或Q(4,32),P(0,72)或Q(−4,−32),P(0,−72).
【解析】
【分析】
此题是反比例函数综合题,主要考查了待定系数法,全等三角形的判定和性质,平行四边形的性质,用分类讨论的思想和方程的思想解决问题是解本题的关键.
(1)先求出OA=6,OG=7,DG=3,再判断出△DGA≌△AHB(AAS),得出DG=AH=3,BH=AG=1,即可得出结论;
(2)先根据运动表示出点B′,D′的坐标,进而求k,t,即可得出结论;
(3)先求出点B′,D′的坐标,再分三种情况,利用平行四边形的对角线互相平分建立方程求解即可得出结论.
【解答】
解:(1)如图,
过点B、D分别作BH⊥x轴、DG⊥x轴交于点H、G,
∵点A(−6,0)、D(−7,3),
∴OA=6,OG=7,DG=3,
∴AG=OG−OA=1,
∵∠DAG+∠BAH=90°,∠DAG+∠GDA=90°,
∴∠GDA=∠BAH,
又∠DGA=∠AHB=90°,AD=AB,
∴△DGA≌△AHB(AAS),
∴DG=AH=3,BH=AG=1,
∴点B坐标为(−3,1);
(2)见答案;
(3)见答案.
25.【答案】解:(1)∵y与x满足反比例函数关系,
∴设y=kx,将点(2,100)代入,
解得k=200,
∴y=200x.
(2)设该车队每天至少要运送m吨物资,
则5m≥200,
则m≥40,
∴该车队每天至少要运送40吨物资.
(3)设该车队原计划每天运送的货物n吨,
则实际每天运送的货物为(1+25%)n吨,
根据题意列方程得,
200(1+25%)n+1=200n,
解得n=40,
经检验,n=40是原方程的根,
∴原计划每天运送货物40吨,实际每天运送货物50吨,
∴实际完成运送任务的天数是20050=4(天).
【解析】(1)设反比函数的解析式,代入(2,100)即可求解;
(2)设该车队每天至少要运送m吨物资,根据题意列不等式,解不等式即可;
(3)设原计划每天运送货物n吨,根据题意列分式方程,即可求出.
本题考查了反比例函数、不等式和分式方程,通过反比例函数确定总的运送任务再根据题意列出相应的分式方程,是解决问题的关键,本题综合性很强.
数学九年级上册1.1 反比例函数优秀单元测试同步达标检测题: 这是一份数学九年级上册1.1 反比例函数优秀单元测试同步达标检测题,共31页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
初中第3章 图形的相似综合与测试单元测试课后测评: 这是一份初中第3章 图形的相似综合与测试单元测试课后测评
初中数学第1章 反比例函数综合与测试单元测试课后作业题: 这是一份初中数学第1章 反比例函数综合与测试单元测试课后作业题