必修 第一册4.5 函数的应用（二）教学课件ppt

这是一份必修 第一册4.5 函数的应用（二）教学课件ppt，文件包含452用二分法求方程的近似解pptx、452用二分法求方程的近似解DOCX等2份课件配套教学资源，其中PPT共44页， 欢迎下载使用。

1.探索用二分法求方程近似解的思路.2.能借助计算工具用二分法求方程近似解.
通过本节内容的学习，使学生体会“逐步逼进”的方法，提升学生数学抽象、逻辑推理、数学运算素养.
问题导学预习教材必备知识探究
互动合作研析题型关键能力提升
拓展延伸分层精练核心素养达成
WEN TI DAO XUE YU XI JIAO CAI BI BEI ZHI SHI TAN JIU
问题导学预习教材 必备知识探究
一、二分法1.问题　在一档娱乐节目中，主持人让选手在规定时间内猜某物品的价格， 若猜中了，就把物品奖给选手.某次竞猜的物品为价格在1 000元之内的一款手机，选手开始报价，选手说“800”，主持人说“高了”；选手说“400”，主持人说“低了”.(1)如果是你，你知道接下来如何竞猜吗？提示　接下来应猜“600”，即区间[400，800]的中点值.(2)通过这种方法能猜到具体价格吗？提示　可以，通过不断地缩小价格所在的区间，直接猜到手机的价格.
2.填空　对于在区间[a，b]上图象连续不断且_______________的函数y＝f(x)，通过不断地把它的零点所在区间__________，使所得区间的两个端点______________，进而得到零点近似值的方法叫做二分法.温馨提醒　二分法的依据是零点存在定理，仅适用于函数的变号零点(函数图象通过零点时函数值的符号变号，如求函数f(x)＝(x－1)2的零点近似值就不能用二分法).
f(a)·f(b)<0
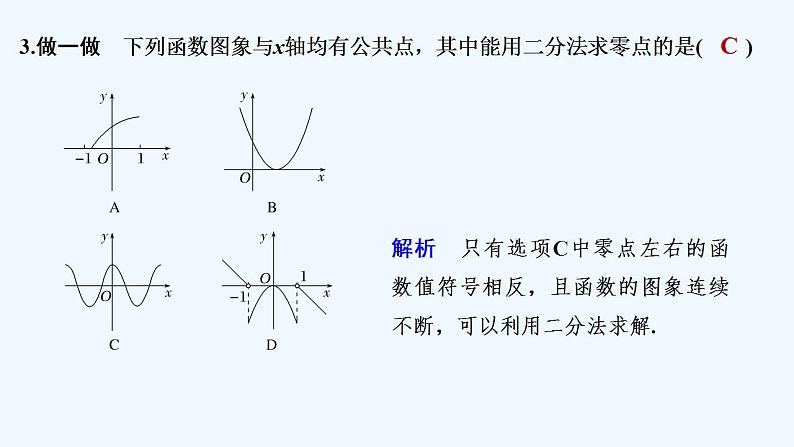
3.做一做　下列函数图象与x轴均有公共点，其中能用二分法求零点的是(　　)
解析　只有选项C中零点左右的函数值符号相反，且函数的图象连续不断，可以利用二分法求解.
二、用二分法求方程的近似解1.问题　假设已知函数f(x)＝ex－3x的零点在区间(1，2)内，如何缩小零点所在区间的范围？提示　取区间(1，2)的中点值1.5；计算f(1.5)的值；验证f(1.5)·f(2)<0是否成立，若成立，则f(x)的零点在区间(1.5，2)内，否则在区间(1，1.5)内.
2.填空　给定精确度ε，用二分法求函数y＝f(x)零点x0的近似值的步骤：(1)确定零点x0的初始区间[a，b]，验证_______________；(2)求区间(a，b)的中点____；(3)计算f(c)，进一步确定零点所在的区间：①若f(c)＝0(此时x0＝c)，则____就是函数的零点；②若f(a)·f(c)<0(此时x0∈_______)，则令b＝c；③若f(c)·f(b)<0(此时x0∈_______)，则令a＝c.(4)判断是否达到精确度ε：若|a－b|<ε，则得到零点近似值a(或b)；否则重复(2)～(4).
温馨提醒　二分法采用逐步逼近的思想，使函数零点所在的范围逐步缩小，也就是逐渐逼近函数的零点.要根据函数的性质尽可能地找到含有零点的更小的区间，注意两点：(1)初始区间的确定要包含函数的变号零点；(2)精确度ε表示当区间的长度小于ε时停止二分.
3.做一做　用二分法求函数f(x)的一个正实数零点时，经计算f(0.64)<0，f(0.72)>0，f(0.68)<0，则函数的一个精确度为0.1的正实数零点的近似值为(　　)A.0.9 B.0.7 C.0.5 D.0.4解析　由题意可知函数的零点在(0.68，0.72)内，四个选项中只有0.7，满足|0.7－0.68|<0.1.
4.思考辨析　正确的在后面的括号内打“√”，错误的打“×”.(1)二分法所求出的方程的解都是近似解.( )(2)函数f(x)＝|x|可以用二分法求零点.( )(3)用二分法求函数零点的近似值时，每次等分区间后，零点必定在右侧区间内.( )(4)若给定的精确度为0.001，则当|a－b|<0.001时即可得到零点近似值.( )
HU DONG HE ZUO YAN XI TI XING GUAN JIAN MENG LI TI SHENG
互动合作研析题型 关键能力提升
例1　(1)(多选)下列函数图象与x轴均有交点，能用二分法求函数零点近似值的是(　 　)
题型一　二分法概念的理解
解析　根据二分法的定义，知函数f(x)在区间[a，b]上的图象连续不断，且f(a)·f(b)<0，即函数的零点是变号零点，才能将区间[a，b]一分为二，逐步得到零点的近似值.对各图象分析可知，选项A，B，C都符合条件，而选项D不符合，因为零点左右两侧的函数值不变号，所以不能用二分法求函数零点的近似值.
(2)用二分法求函数f(x)＝2x＋3x－7在区间[0，4]上的零点近似值，取区间的中点2，则下一个存在零点的区间为(　　)A.(0，1) B.(0，2)C.(2，3) D.(2，4)解析　因为f(0)＝20＋0－7＝－6<0，f(4)＝24＋12－7>0，f(2)＝22＋6－7>0，所以f(0)f(2)<0.所以零点所在区间为(0，2).
运用二分法求函数的零点应具备的条件(1)函数图象在零点附近连续不断.(2)在该零点左右函数值异号.只有满足上述两个条件，才可用二分法求函数零点.
训练1 已知函数f(x)的图象如图，其中零点的个数与可以用二分法求解的零点个数分别为(　　)
A.4，4 B.3，4C.5，4 D.4，3解析　因为图象与x轴有4个交点，所以零点的个数为4；又因为左、右函数值异号的有3个零点，所以可以用二分法求解的零点个数为3.
例2 用二分法求方程2x3＋3x－3＝0的一个正实数近似解(精确度是0.1).解　令f(x)＝2x3＋3x－3，经计算，f(0)＝－3<0，f(1)＝2>0，f(0)·f(1)<0，所以函数f(x)在(0，1)内存在零点，即方程2x3＋3x－3＝0在(0，1)内有解.取(0，1)的中点0.5，经计算f(0.5)<0，又f(1)>0，所以方程2x3＋3x－3＝0在(0.5，1)内有解.如此继续下去，得到方程的正实数解所在的区间，如下表：
题型二　用二分法求方程的近似解
由于|0.687 5－0.75|＝0.062 5<0.1，所以方程2x3＋3x－3＝0的一个精确度为0.1的正实数近似解可取为0.75.
用二分法求方程的近似解，首先要选好计算的初始区间，这个区间既要包含所求的根，又要使其长度尽量小，其次要依据给定的精确度，及时检验所得区间的长度是否达到要求(达到给定的精确度)，以决定是停止计算还是继续计算.
训练2 用二分法求方程ln(2x＋6)＋2＝3x的解的近似值时，令f(x)＝ln(2x＋6)＋2－3x，并用计算器得到下表：
由表中的数据，求方程ln(2x＋6)＋2＝3x的一个近似解.(精确度为0.1)解　因为f(1.25)·f(1.375)<0，所以根据二分法的思想，可知函数f(x)的零点在区间(1.25，1.375)内.但区间(1.25，1.375)的长度为0.125>0.1，因此需要取区间(1.25，1.375)的中点1.312 5，两个区间(1.25，1.312 5)和(1.312 5，1.375)中必有一个满足区间端点的函数值符号相异.又区间的长度为0.062 5<0.1，因此1.312 5是一个近似解.
题型三　二分法的实际应用
例3 某市A地到B地的电话线路发生故障，这是一条10 km长的线路，每隔50 m有一根电线杆，如何迅速查出故障所在？解　如图，可首先从中点C开始查起，用随身携带的工具检查，若发现AC段正常，则断定故障在BC段；
再到BC段的中点D检查，若CD段正常，则故障在BD段；再到BD段的中点E检查，如此，每检查一次就可以将待查的线路长度缩短一半，经过7次查找，即可将故障范围缩小到50 m～100 m之间，即可迅速找到故障所在.
二分法的思想在实际生活中应用十分广泛，二分法不仅可用于线路、水管、煤气管道故障的排查，还能用于实验设计、资料查询、资金分配等.
训练3 在12枚崭新的金币中，有一枚外表与真币完全相同的假币(质量小一点)，现在只有一台天平，则应用二分法的思想，最多称________次就可以发现这枚假币.解析　将12枚硬币平均分成两份，放在天平上，假币在轻的那6枚硬币里面；将这6枚平均分成两份，则假币一定在轻的那3枚硬币里面；将这3枚硬币任拿出2枚放在天平上，若平衡，则剩下的那一枚即是假币；若不平衡，则轻的那一枚即是假币.依据上述分析，最多称3次就可以发现这枚假币.
1.二分法就是通过不断地将所选区间一分为二，使区间的两个端点逐步逼近零点，直至找到零点附近足够小的区间，根据所要求的精确度，用此区间的某个数值近似地表示真正的零点.2.并非所有函数都可以用二分法求其零点，只有满足：(1)在区间[a，b]上连续不断；(2)f(a)·f(b)<0.上述两条的函数，方可采用二分法求得零点的近似值.
TUO ZHAN YAN SHEN FEN CENG JING LIAN HE XING SU YANG DA CHENG
拓展延伸分层精练 核心素养达成
1.已知定义在R上的函数f(x)的图象是连续不断的，且有如下对应值表：
那么函数f(x)一定存在零点的区间是(　　)A.(0，1) B.(1，2) C.(2，3) D.(3，＋∞)解析　因为f(1)f(2)<0，所以f(x)在(1，2)内一定存在零点.
2.以下每个图象表示的函数都有零点，但不能用二分法求函数零点的是(　　)
解析　根据二分法的思想，函数f(x)在区间[a，b]上的图象连续不断，且f(a)·f(b)<0，即函数的零点是变号零点，才能将区间[a，b]一分为二，逐步得到零点的近似值，对各图象分析可知，A，B，D都符合条件.而选项C不符合，因为图象经过零点时函数值不变号，因此不能用二分法求函数零点.
3.在用“二分法”求函数f(x)零点近似值时，第一次所取的区间是[－2，4]，则第三次所取的区间可能是(　　)
解析　∵第一次所取的区间是[－2，4]，∴第二次所取的区间可能为[－2，1]，[1，4]，
4.(多选)用二分法求函数f(x)＝5x＋7x－2的一个零点，其参考数据如下：
根据上述数据，可得f(x)＝5x＋7x－2的一个零点近似值(精确度0.05)为(　 　) 75 解析　已知f(0.093 75)<0，f(0.125)>0，则函数f(x)的零点的初始区间为(0.093 75，0.125)，所以零点在区间(0.093 75，0.125)上，|0.125－0.093 75|＝0.031 25<0.05，所以0.093 75，0.096，0.125都符合题意.
6.用二分法求方程x3－2x－5＝0在区间(2，4)上的实数根时，取中点x1＝3，则下一个有根区间是________.解析　设函数f(x)＝x3－2x－5，∵f(2)＝－1<0，f(3)＝16>0，f(4)＝51>0，∴下一个有根区间是(2，3).
7.用二分法求函数f(x)＝ln x＋2x－6在区间(2，3)内的零点近似值，至少经过________次二分后精确度达到0.1.
8.函数f(x)＝x2＋ax＋b有零点，但不能用二分法求出，则a，b的关系是_____________.解析　∵函数f(x)＝x2＋ax＋b有零点，但不能用二分法求出，∴函数f(x)＝x2＋ax＋b的图象与x轴相切，∴Δ＝a2－4b＝0，∴a2＝4b.
9.用二分法求2x＋x＝4在[1，2]内的近似解(精确度为0.2).参考数据：
解　令f(x)＝2x＋x－4，则f(1)＝2＋1－4<0，f(2)＝22＋2－4>0.用二分法的思想，列表如下：
∵|1.375－1.5|＝0.125<0.2，∴2x＋x＝4在[1，2]内的近似解可取为1.375.
10.从A地到B地的海底电缆有15个接点，现某一个接点发生故障，需及时修理，为了尽快找到故障的发生点，一般最多需要检查多少个接点？解　先检查中间的1个接点，若正常，则可断定故障在其另一侧的7个接点中；然后检查这一段中间的1个接点，若仍正常，则可断定故障在其另一侧的3个接点中；最后只需检查这3个接点中间的1个，即可找出故障所在.故一般最多只需检查3个接点.
11.在用二分法求函数f(x)的一个正实数零点时，经计算f(0.64)<0，f(0.72)>0，f(0.68)<0，则函数的一个精确度为0.05的正实数零点的近似值不可以为(　　) C.0.7 D.0.6解析　已知f(0.64)<0，f(0.72)>0，
所以零点在区间(0.68，0.72)上，|0.72－0.68|＝0.04<0.05，所以0.68，0.7，0.72都符合.
∴f(x)的零点x0∈(1，2)，故n＝1.设至少需等分n次，
解得n≥7，故至少需等分7次.
13.某同学在借助计算器求方程lg x＝2－x的近似解(精确度为0.1)时，设f(x)＝lg x＋x－2，算得f(1)<0，f(2)>0，然后他用二分法又取了4个x的值，计算了函数值，并得出判断：方程的近似解x≈1.8，那么他之后取的x的4个值依次是____________________________.解析　第一次用二分法计算得区间(1.5，2)，第二次得区间(1.75，2)，第三次得区间(1.75，1.875)，第四次得区间(1.75，1.812 5)，此时|1.812 5－1.75|＝0.062 5<0.1，且1.812 5≈1.8，1.75≈1.8，故他之后取的x的4个值依次是1.5，1.75，1.875，1.812 5.
1.5，1.75，1.875，1.812 5
14.已知函数f(x)＝3ax2＋2bx＋c，a＋b＋c＝0，f(0)>0，f(1)>0，证明a>0，并利用二分法证明方程f(x)＝0在区间[0，1]内有两个实根.证明　∵f(1)>0，∴3a＋2b＋c>0，则3(a＋b＋c)－b－2c>0.∵a＋b＋c＝0，∴－b－2c>0，则－b－c>c，即a>c.∵f(0)>0，∴c>0，则a>0.
∵f(0)>0，f(1)>0，
又f(x)最多有两个零点.故方程f(x)＝0在区间[0，1]内有两个实根.