









高中人教A版 (2019)3.2 函数的基本性质教学演示课件ppt
展开人教A版(2019)高中数学必修第一册
3.2.2 第1课时奇偶性概念教学设计
课题名 | 3.2.2 第1课时奇偶性概念 | |||||||||
教学目标 | 1.了解函数奇偶性的含义. 2.掌握判断函数奇偶性的方法,了解奇偶性与函数图象对称性之间的关系. 3.会利用函数的奇偶性解决简单问题. | |||||||||
教学重点 | 会利用函数的奇偶性解决简单问题 | |||||||||
教学难点 | 了解函数奇偶性的含义 | |||||||||
教学准备 | 教师准备:幻灯片、黑板、投影 学生准备:笔、纸、课本 | |||||||||
教学过程 | 一、 新课引入
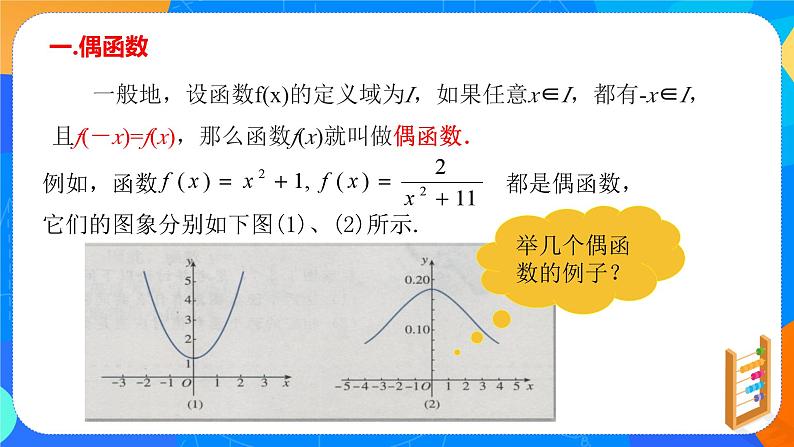
观察以上函数图象,从图象对称的角度把这些函数图象分类 二、讲授新课 偶函数 一般地,设函数f(x)的定义域为I,如果任意x∈I,都有-x∈I, 且f(-x)=f(x),那么函数f(x)就叫做偶函数.
奇函数 一般地,设函数f(x)的定义域为I,如果任意x∈I,都有-x∈I,且f(-x)=-f(x),那么函数f(x)就叫做奇函数. 1、函数的奇偶性是函数的整体性质(单调性是局部性质) 2、由函数的奇偶性定义可知,任意x∈I,都有-x∈I(即定义域关于原点对称). 3、若f(x)为奇函数, 0∈I,一定有f(0)=0. 【小试牛刀】 1.思辨解析(正确的打“√”,错误的打“×”) (1)对于函数y=f(x),若存在x,使f(-x)=-f(x),则函数y=f(x)一定是奇函数.( ) (2)不存在既是奇函数,又是偶函数的函数.( ) (3)若函数的定义域关于原点对称,则这个函数不是奇函数,就是偶函数.( ) (4)函数f(x)=x2,x∈[0,+∞)是偶函数. ( ) (1)× (2)× (3)× (4)×
2.下列图象表示的函数是奇函数的是________,是偶函数的是________.(填序号)
题型一 函数奇偶性的判断 函数奇偶性判断的方法: (1)定义法:
(2)图象法:
例1 判断下列函数的奇偶性: (1)f(x)=x3+x; (2)f(x)=+; (3)f(x)=; (4)f(x)= 解:(1)函数的定义域为R,关于原点对称. 又f(-x)=(-x)3+(-x)=-(x3+x)=-f(x), 因此函数f(x)是奇函数. (2)由得x2=1,即x=±1. 因此函数的定义域为{-1,1},关于原点对称. 又f(1)=f(-1)=-f(-1)=0, 所以f(x)既是奇函数又是偶函数. (3)函数f(x)的定义域是(-∞,-1)∪(-1,+∞), 不关于原点对称,所以f(x)既不是奇函数也不是偶函数. (4)函数f(x)的定义域为R,关于原点对称. f(-x)= 即f(-x)= 于是有f(-x)=-f(x). 【跟踪训练】1 判断下列函数的奇偶性: (1)f(x)=x2(x2+2); (2)f(x)=|x+1|-|x-1|; (3)f(x)=; (4)f(x)= 解:(1)∵x∈R,∴-x∈R. 又∵f(-x)=(-x)2[(-x)2+2]=x2(x2+2)=f(x), ∴f(x)为偶函数. (2)∵x∈R,∴-x∈R.又∵f(-x)=|-x+1|-|-x-1| =|x-1|-|x+1|=-(|x+1|-|x-1|)=-f(x), ∴f(x)为奇函数. (3)f(x)的定义域为[-1,0)∪(0,1].即有-1≤x≤1且x≠0, 则-1≤-x≤1,且-x≠0, 又∵f(-x)==-=-f(x), ∴f(x)为奇函数. (4)f(x)的定义域是(-∞,0)∪(0,+∞),关于原点对称. 当x>0时,-x<0,f(-x)=1-(-x)=1+x=f(x); 当x<0时,-x>0,f(-x)=1+(-x)=1-x=f(x). 综上可知,对于x∈(-∞,0)∪(0,+∞), 都有f(-x)=f(x),f(x)为偶函数. 题型二 奇、偶函数的图象问题 点拨:根据奇偶函数在原点一侧的图象求解与函数有关的值域、定义域、不等式问题时,应根据奇偶函数图象的对称性作出函数在定义域另一侧的图象,根据图象特征求解问题. 例2 已知奇函数f(x)的定义域为[-5,5],且在区间[0,5]上的图象如图所示. (1)画出f(x)在区间[-5,0]上的图象; (2)写出使f(x)<0的x的取值集合. 解 (1)因为函数f(x)是奇函数,所以y=f(x)在[-5,5]上的图象关于原点对称.由y=f(x)在[0,5]上的图象,可知它在[-5,0]上的图象,如图所示. (2)由图象知,使函数值f(x)<0的x的取值集合为(-2,0)∪(2,5). 【跟踪训练】2 如图,给出了偶函数y=f(x)的局部图象,试比较f(1)与f(3)的大小. 解:方法一 因函数f(x)是偶函数, 所以其 图象关于y轴对称,补全图 如图.
由图象可知f(1)<f(3). 方法二 由图象可知f(-1)<f(-3). 又函数y=f(x)是偶函数,所以f(-1)=f(1),f(-3)=f(3), 故f(1)<f(3). 题型三 函数奇偶性的应用 例3-1 (利用奇偶性求函数值)已知f(x)=x5+ax3+bx-8,若f(-3=10,则f(3)=( ) A.26 B.18 C.10 D.-26 解析 由f(x)=x5+ax3+bx-8,得f(x)+8=x5+ax3+bx. 令G(x)=x5+ax3+bx=f(x)+8, ∵G(-x)=(-x)5+a(-x)3+b(-x) =-(x5+ax3+bx)=-G(x), ∴G(x)是奇函数,∴G(-3)=-G(3), 即f(-3)+8=-f(3)-8.又f(-3)=10, ∴f(3)=-f(-3)-16=-10-16=-26. 例3-2 (利用奇偶性求参数值) 若函数f(x)=为奇函数,则a=________. 解析∵f(x)是奇函数,∴f(-x)=-f(x),即=-,显然x≠0,整理得x2-(a+1)x+a=x2+(a+1)x+a,故a+1=0,解得a=-1. 【跟踪训练】3 (1)已知f(x)=x7-ax5+bx3+cx+2,若f(-3)=-3,则f(3)=________. (2)若函数f(x)=ax2+bx+3a+b是偶函数,定义域为[a-2,2a],则a=_____,b=______。 解析: (1)令g(x)=x7-ax5+bx3+cx,则g(x)是奇函数, ∴f(-3)=g(-3)+2=-g(3)+2,又f(-3)=-3, ∴g(3)=5.又f(3)=g(3)+2,所以f(3)=5+2=7. (2)由f(x)为偶函数知,其定义域关于原点对称, 故有a-2+2a=0,解得a=. 又f(x)为偶函数,所以其图象关于y轴对称, 即-=0,解得b=0. 三、课堂小结 1.函数的奇偶性 (1)定义域特点:关于原点对称; (2)图象特点:偶函数关于y轴对称;奇函数关于原点对称; (3)解析式特点:偶函数满足f(-x)=f(x)或f(x)-f(-x)=0,奇函数 满足f(-x)=-f(x)或f(x)+f(-x)=0. 2.判断函数奇偶性的方法 (1)定义法;(2)图象法. 四、当堂检测 1.函数f(x)=|x|+1是( ) A.奇函数 B.偶函数 C.既是奇函数又是偶函数 D.非奇非偶函数 解析:∵f(-x)=|-x|+1=|x|+1=f(x),∴f(x)为偶函数. 2.f(x)=x3+的图象关于( ) A.原点对称 B.y轴对称 C.y=x对称 D.y=-x对称 解析:f(x)的定义域为(-∞,0)∪(0,+∞),关于原点对称. 又f(-x)=(-x)3+=-x3-=-(x3+)=-f(x), ∴f(x)是奇函数,∴其图象关于原点对称. 3.(多选题)设函数f(x),g(x)的定义域都为R,且f(x)是奇函数,g(x)是偶函数,则下列结论中正确的是( ) A.f(x)g(x)是奇函数 B.|f(x)|g(x)是偶函数 C.f(x)|g(x)|是偶函数 D.|f(x)g(x)|是偶函数 解析:∵f(x)是奇函数,g(x)是偶函数,∴|f(x)|为偶函数, |g(x)|为偶函数. 再根据两个奇函数的积是偶函数、两个偶函数的积还是偶 函数、一个奇函数与一个偶函数的积是奇函数,可得A为奇函数,B为偶函数,C为奇函数;D为偶函数.] 4.已知函数f(x)=x2+(2-m)x+m2+12为偶函数,则m的值是( ) A.4 B.3 C.2 D.1 解析:因为函数f(x)=x2+(2-m)x+m2+12为偶函数, 所以f(x)=f(-x),即x2+(2-m)x+m2+12 =(-x)2-(2-m)x+m2+12, 即4-2m=0,所以m=2. 5.已知函数f(x)是定义域为R的奇函数,且f(-1)=2,则f(0)+f(1)= . 解析:∵f(x)为R上的奇函数,∴f(0)=0,f(1)=-f(-1)=-2, ∴f(0)+f(1)=0-2=-2. 6.已知函数y=f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图象,如图所示. (1)请补出完整函数y=f(x)的图象; (2)根据图象写出函数y=f(x)的增区间; (3)根据图象写出使f(x)<0的x的取值集合. 解:(1)由题意作出函数图象如图: (2)据图可知,单调增区间为(-1,0),(1,+∞). (3)据图可知,使f(x)<0的x的取值集合为(-2,0)∪(0,2). | |||||||||
布置作业 | 完成对应的课后练习 | |||||||||
板书设计 |
| |||||||||
教学反思 | 学生总体上都可以掌握这次内容,不过课后还需要多加练习去巩固所学的知识。 |
高中数学人教A版 (2019)必修 第一册3.2 函数的基本性质图片ppt课件: 这是一份高中数学人教A版 (2019)必修 第一册3.2 函数的基本性质图片ppt课件,共25页。PPT课件主要包含了f-3f3,f-2f2,f-1f1,g-3g3,g-2g2,g-1g1,定义域关于原点对称,1fxx4,2fxx5,方法总结等内容,欢迎下载使用。
高中数学3.2 函数的基本性质图文ppt课件: 这是一份高中数学3.2 函数的基本性质图文ppt课件,共50页。PPT课件主要包含了新知初探课前预习,-Fx,答案C,答案B,题型探究课堂解透,-26,acb,答案D,易错警示,答案AD等内容,欢迎下载使用。
高中数学人教A版 (2019)必修 第一册3.2 函数的基本性质完美版ppt课件: 这是一份高中数学人教A版 (2019)必修 第一册3.2 函数的基本性质完美版ppt课件,文件包含322第1课时奇偶性的概念ppt、322第1课时奇偶性概念教学设计docx等2份课件配套教学资源,其中PPT共32页, 欢迎下载使用。














