数学第21章二次函数与反比例函数21.1 二次函数优秀教学课件ppt

展开

这是一份数学第21章二次函数与反比例函数21.1 二次函数优秀教学课件ppt，共20页。PPT课件主要包含了导入新课，向上平移3个单位，y-2x2+3，向左平移2个单位，y-2x+22，讲授新课，解先列表，直线x－1，直线xh，顶点式等内容，欢迎下载使用。

1.会用描点法画出二次函数y=a(x+h)²+k的图象；2.掌握形如y=a(x+h)²+k的二次函数图象的性质，并会应用；（重点）3.理解y=a(x+h)²+k与 y=ax²之间的联系.（难点）
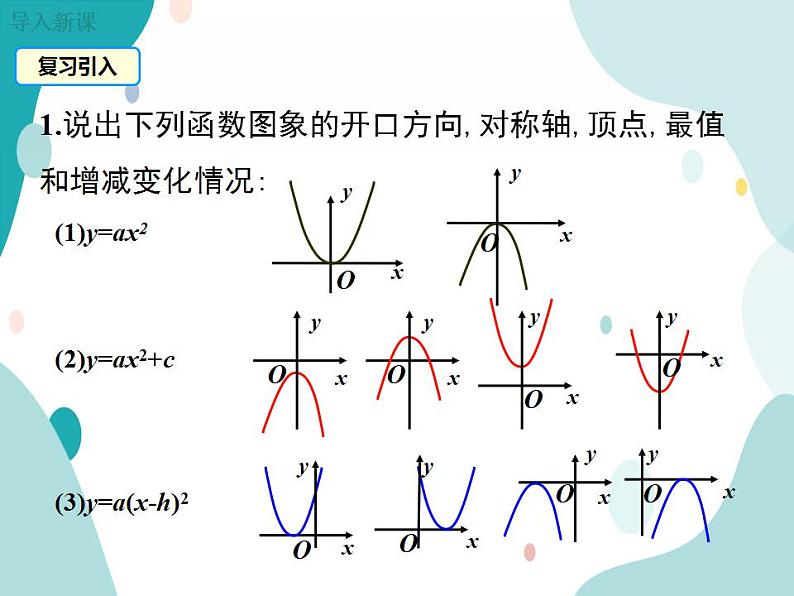
1.说出下列函数图象的开口方向,对称轴,顶点,最值和增减变化情况:
(1)y=ax2(2)y=ax2+c(3)y=a(x-h)2
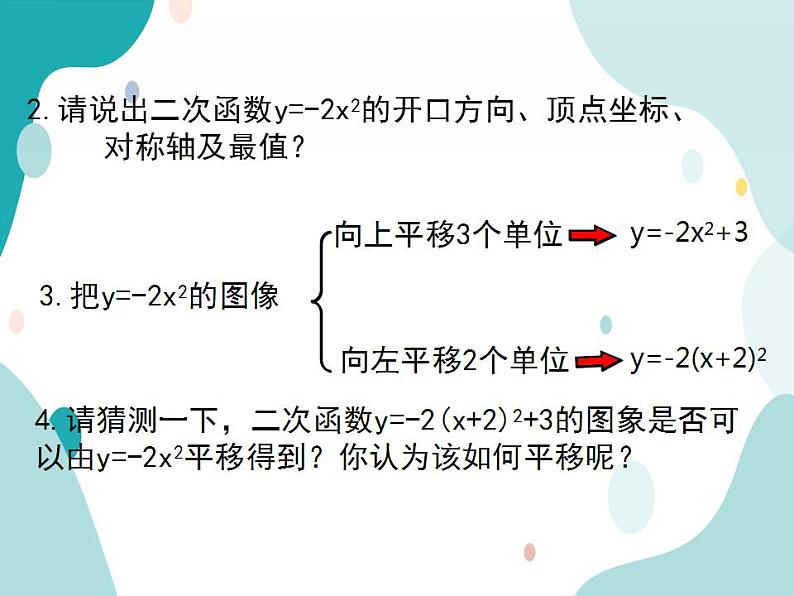
2.请说出二次函数y=-2x2的开口方向、顶点坐标、对称轴及最值？
3.把y=-2x2的图像
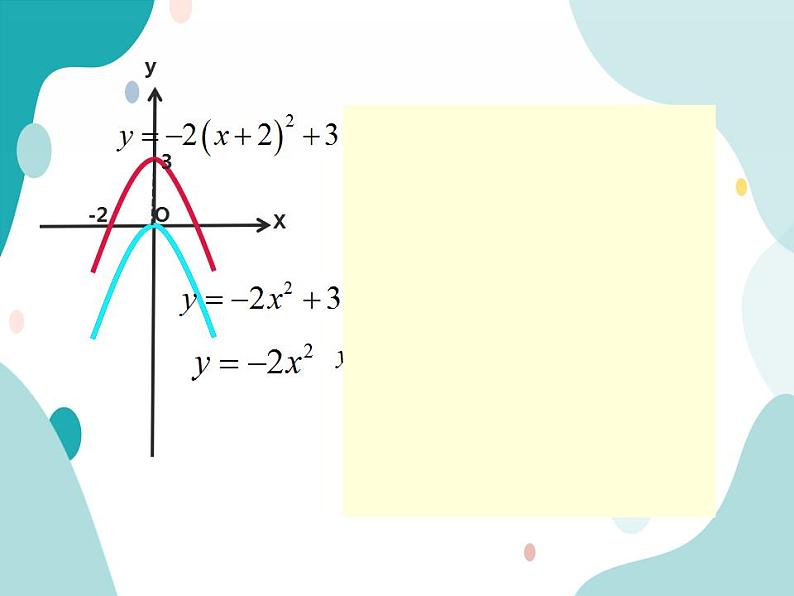
4.请猜测一下，二次函数y=-2(x+2)2+3的图象是否可以由y=-2x2平移得到？你认为该如何平移呢？
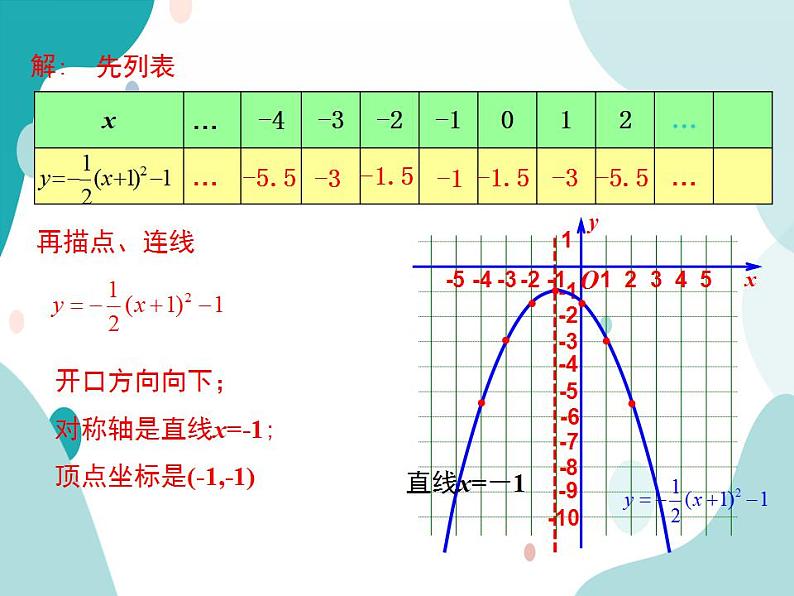
例1 画出函数的图像.指出它的开口方向、顶点与对称轴.
开口方向向下；对称轴是直线x=-1;顶点坐标是(-1,-1)
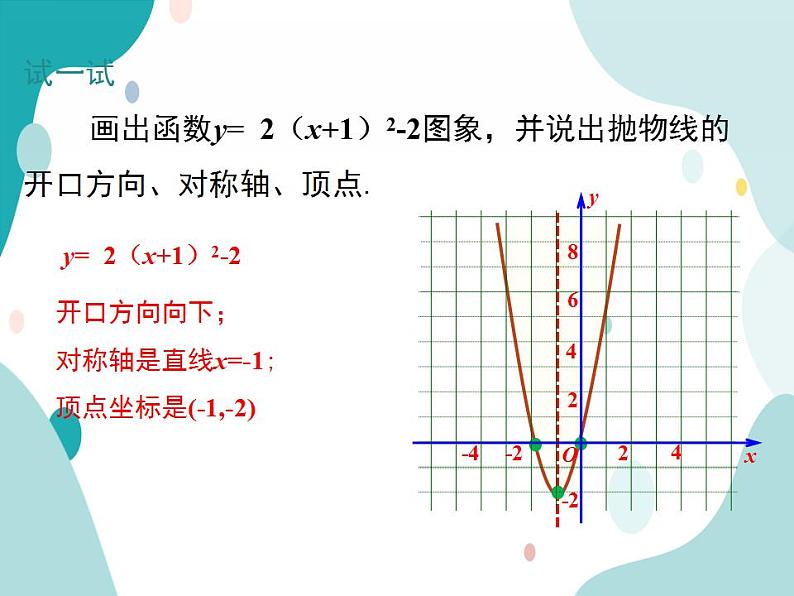
试一试画出函数y= 2（x+1）2-2图象，并说出抛物线的开口方向、对称轴、顶点.
开口方向向下；对称轴是直线x=-1;顶点坐标是(-1,-2)
y= 2（x+1）2-2
二次函数y=a（x+h)2 +k的特点
a＞0时，开口 , 最点是顶点; a＜0时，开口 , 最点是顶点; 对称轴是，顶点坐标是 .
例3. 已知二次函数y＝a(x－1)2－4的图象经过点(3，0)．(1)求a的值；(2)若A(m，y1)、B(m＋n，y2)(n＞0)是该函数图象上的两点，当y1＝y 2时，求m、n之间的数量关系．
分析：(1)把点(3，0)的坐标代入函数表达式计算即可得解；(2)方法一：根据y1＝y2列出关于m、n的方程，然后开方整理即可得解；方法二：根据二次函数的对称性列出关于m、n的方程，然后整理即可得解．
解：(1)将(3，0)代入y＝a(x－1)2－4，得0＝4a－4，解得a＝1；
(2)方法一：根据题意，得y1＝(m－1)2－4，y2＝(m＋n－1)2－4， ∵y1＝y2，∴(m－1)2－4＝(m＋n－1)2－4，即(m－1)2＝(m＋n－1)2.∵n＞0，∴m－1＝－(m＋n－1)，化简，得2m＋n＝2；方法二：∵函数y＝(x－1)2－4的图象的对称轴是经过点(1，－4)，且平行于y轴的直线，∴m＋n－1＝1－m，化简，得2m＋n＝2.
方法总结：已知函数图象上的点，则这点的坐标必满足函数的表达式，代入即可求得函数解析式．
二次函数y=ax2 与y=a（x+h)2+k的关系
可以看作互相平移得到的.
y = ax2 + k
y = a(x - h )2
y = a( x - h )2 + k
简记为：上下平移，括号外上加下减；左右平移，括号内左加右减.二次项系数a不变.
1.请回答抛物线y = 4(x－3)2＋7由抛物线y=4x2怎样平移得到?
由抛物线向上平移7个单位再向右平移3个单位得到的.
y=－3(x－1)2－2
y = 4(x－3)2＋7
y=－5(2－x)2－6
2.把抛物线y=-3x2先向上平移2个单位，再向右平移1个单位，那么所得抛物线是___________________.
4.抛物线y=-3(x-1)2+2的图象如何得到y=-3x2 .
3.抛物线y=-3x2+2的图象向右平移2个单位，再向上平移1个单位，得到抛物线的解析式为______________
先向下平移2个单位再向左移1个单位得到.（或先向左移1个单位再向下平移2个单位）
5.已知一个二次函数图象的顶点为A(-1,3),且它是由二次函数y=5x2平移得到，请直接写出该二次函数的解析式.
y=a(x-h)2+k

相关课件更多