









高中数学人教A版 (2019)必修 第一册第三章 函数概念与性质3.2 函数的基本性质评课ppt课件
展开人教A版(2019)高中数学必修第一册
3.2.1第2课时函数的最大(小)值教学设计
课题名 | 3.2.1第2课时函数的最大(小)值 |
教学目标 | 1.理解函数的最大(小)值的概念及其几何意义. 2.会借助单调性求最值. 3.掌握求二次函数在闭区间上的最值 |
教学重点 | 掌握求二次函数在闭区间上的最值 |
教学难点 | 理解函数的最大(小)值的概念及其几何意义 |
教学准备 | 教师准备:幻灯片、黑板、投影 学生准备:笔、纸、课本 |
教学过程 | 一、 新课引入 下列两个函数的图象:
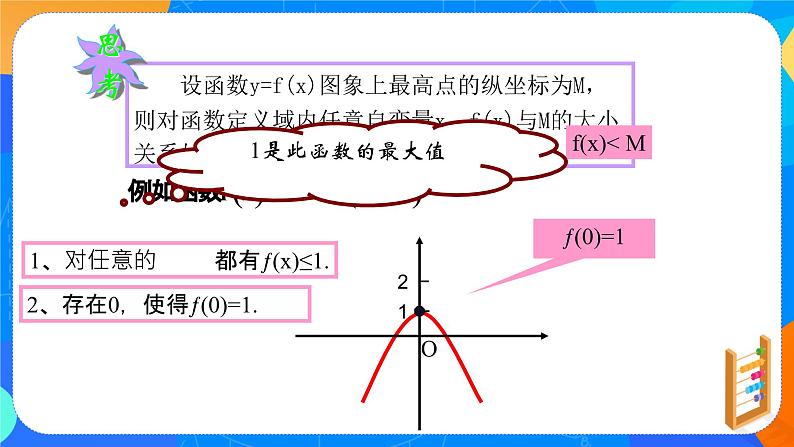
观察这两个函数图象,图中有个最高点,那么这个最高点的纵坐标叫什么呢? 设函数y=f(x)图象上最高点的纵坐标为M,则对函数定义域内任意自变量x,f(x)与M的大小关系如何? 二、讲授新课 函数的最大值 一般地,设函数y=f(x)的定义域为I,如果存在实数M满足: (1)∀x∈I,都有 f(x)≤M ; (2)∃x0∈I,使得 f(x0)=M . 那么,我们称M是函数y=f(x)的最大值,记作f(x)max=M. 函数的最小值 一般地,设函数y=f(x)的定义域为I,如果存在实数N满足: x∈I,都有f(x)≥N ; ∃x0∈I,使得f(x0)=N,就称N是函数y=f(x)的最小值,记作f(x)min=N. 思考1:函数f(x)=-x2≤1总成立吗? f(x)的最大值是1吗? f(x)=-x2≤1总成立,但是不存在x0使f(x0)=1,所以f(x)的最大值不是1,而是0. 思考2:函数的最值与函数的值域有什么关系? 函数值域是指函数值的集合,函数最大(小)值一定是值域的元素.如果值域是一个闭区间,那么函数的最大(小)值就是闭区间两端点的值. 【小试牛刀】 思辨解析(正确的打“√”,错误的打“×”) (1)因为f(x)=x2+1≥0恒成立,所以f(x)的最小值为0.( ) (2)任何函数都有最大(小)值.( ) (3)函数f(x)取最大值时,对应的x可能有无限多个.( ) (4)如果f(x)的最大值、最小值分别为M,m,则f(x)的值域为[m,M].( ) × × √ × 题型一 图象法求函数的最值 点拨:图象法求最值的一般步骤 ①画出函数图象; ②观察图象,找出图象的最高点和最低点; ③写出最值,最高点的纵坐标是函数的最大值,最低点的纵坐标是函数的最小值.) 例1 如图所示为函数y=f(x),x∈[-4,7]的图象,指出它的最大值、最小值及单调区间. 解:观察函数图象可以知道,图象上位置最高的点是(3,3),最低的点是(-1.5,-2),所以函数y=f(x)当x=3时取得最大值,最大值是3.当x=-1.5时取得最小值,最小值是-2.函数的单调递增区间为[-1.5,3),[5,6),单调递减区间为[-4,-1.5),[3,5),[6,7].
【跟踪训练】1 已知函数f(x)=则f(x)的最大值为________. 解析:f(x)的图象如图:则f(x)的最大值为f(2)=2. 题型二 利用单调性求函数的最大(小)值 点拨:1.运用函数单调性求最值是求函数最值的常用方法,特别是当函数图象不易作出时,单调性几乎成为首选方法.首先判断函数的单调性,再利用单调性求出最值. 2.①注意对问题中求最值的区间与函数的单调区间之间的关系进行辨析,②注意对问题中求最值的区间的端点值的取舍. 例2 已知f(x)=, (1)判断f(x)在(1,+∞)上的单调性,并加以证明. (2)求f(x)在[2,6]上的最大值和最小值. 解:(1)函数f(x)在(1,+∞)上是减函数. 证明:任取x2>x1>1,则f(x1)-f(x2)= -=, 因为x1-1>0,x2-1>0,x2-x1>0, 所以f(x1)-f(x2)>0,即f(x1)>f(x2). 所以f(x)在(1,+∞)上是减函数. (2)由(1)可知f(x)在(1,+∞)上是减函数, 所以f(x)在[2,6]上是减函数, 所以f(x)max=f(2)=1,f(x)min=f(6)=, 即f(x)min=,f(x)max=1.
【跟踪训练】2 已知函数f(x)=,求函数f(x)在[1,5]上的最值. 解:先证明函数f(x)=的单调性,设x1,x2是区间上的任意两个实数,且x2>x1>,f(x1)-f(x2)=-=. 由于x2>x1>,所以x2-x1>0,且(2x1-1)·(2x2-1)>0,所以f(x1)-f(x2)>0,即f(x1)>f(x2),所以函数f(x)=在区间上是减少的,所以函数f(x)在[1,5]上是减少的,因此,函数f(x)=在区间[1,5]的两个端点上分别取得最大值与最小值,即最大值为f(1)=3,最小值为f(5)=. 题型三 求二次函数的最值 点拨:二次函数的最值问题,解题策略一般都是讨论函数的定义域与对称轴的位置关系,往往分三种情况:(1)定义域在对称轴左侧;(2)对称轴在定义域内;(3)定义域在对称轴右侧.在讨论时可结合函数图象,便于分析、理解. 例3-1(定轴定区间类型)已知函数f(x)=x2-2x-3,若x∈[0,2],求函数f(x)的最值。 解:∵函数f(x)=x2-2x-3开口向上,对称轴x=1,∴f(x)在[0,1]上单调递减,在[1,2]上单调递增,且f(0)=f(2).∴f(x)max=f(0)=f(2)=-3,f(x)min=f(1)=-4. 例3-2 (定轴动区间类型)已知函数f(x)=x2-2x-3,若x∈[t,t+2],求函数f(x)的最值。 解:∵对称轴x=1, ①当1≥t+2即t≤-1时,f(x)max=f(t)=t2-2t-3, f(x)min=f(t+2)=(t+2)2-2(t+2)-3=t2+2t-3. ②当≤1<t+2,即-1<t≤0时,f(x)max=f(t) =t2-2t-3,f(x)min=f(1)=-4. ③当t≤1<,即0<t≤1时,f(x)max=f(t+2) =t2+2t-3,f(x)min=f(1)=-4. ④当1<t,即t>1时,f(x)max=f(t+2)=t2+2t-3, f(x)min=f(t)=t2-2t-3. 设函数f(x)的最大值为g(t),最小值为φ(t),则有 g(t)=φ(t)= 例3-3(动轴定区间)求二次函数f(x)=x2-2ax+2在[2,4]上的最小值。 解:∵函数图象的对称轴是x=a,∴当a<2时,f(x)在[2,4]上是增函数,∴f(x)min=f(2)=6-4a. 当a>4时,f(x)在[2,4]上是减函数,∴f(x)min=f(4)=18-8a. 当2≤a≤4时,f(x)min=f(a)=2-a2. ∴f(x)min= 【跟踪训练】3 已知函数f(x)=x-2-3,求函数f(x)的最值. 解:设=t(t≥0),则x-2-3=t2-2t-3.由(1)知y=t2-2t- 3(t≥0)在[0,1]上单调递减,在[1,+∞)上单调递增.∴当t=1即x=1时,f(x)min=-4,无最大值. 三、课堂小结 1.函数的最大(小)值的概念及其几何意义. 2.会借助单调性求最值:注意端点值的选取. 3.掌握求二次函数在闭区间上的最值. 四、当堂检测 1.函数f(x)=-x2-4x+1,x∈[-3,3]的值域是( ) A.(-∞,5] B.[5,+∞) C.[-20,5] D.[4,5] 解析:∵f(x)=-(x+2)2+5,∴当x=-2时,函数有最大值5;当x=3时,函数有最小值-20,故选C. 2.已知函数f(x)=,x∈[-8,-4),则下列说法正确的是( ) A.f(x)有最大值,无最小值 B.f(x)有最大值,最小值 C.f(x)有最大值,无最小值 D.f(x)有最大值2,最小值 解析:f(x)==2+,它在[-8,-4)上单调递减,因此有最大值f(-8)=,无最小值。 3.函数f(x)=的最大值为________. 解析:当x≥1时,函数f(x)=为减函数,所以f(x)在x=1处取得最大值,为f(1)=1;当x<1时,易知函数f(x)=-x2+2在x=0处取得最大值,为f(0)=2.故函数f(x)的最大值为2. 4.函数f(x)=在[1,b](b>1)上的最小值是,则b=________. 解析:因为f(x)在[1,b]上是减函数,所以f(x)在[1,b]上的最小值为f(b)==,所以b=4. 5.求函数f(x)=x2-4x-4在闭区间[t,t+1](t∈R)上的最小值. 解:f(x)=x2-4x-4=(x-2)2-8. 设f(x)在[t,t+1]上的最小值为g(t). 当t>2时,f(x)在[t,t+1]上是增函数, ∴g(t)=f(t)=t2-4t-4; 当t≤2≤t+1,即1≤t≤2时,g(t)=f(2)=-8; 当t+1<2即t<1时,f(x)在[t,t+1]上是减函数, ∴g(t)=f(t+1)=t2-2t-7. 综上,g(t)= 6.已知函数f(x)=,x∈[3,5]. (1)判断函数在区间[3,5]上的单调性,并给出证明; (2)求该函数的最大值和最小值.
|
布置作业 | 完成对应课后练习 |
板书设计 | 1.函数最大、最小值的概念 2.利用单调性求最值 3.二次函数的最值 |
教学反思 | 学生总体上都可以掌握这次内容,不过对于二次函数的最值这一块还需要加强,特别是动轴定区间、定轴定区间等情况下求最值。 |
高中数学人教A版 (2019)必修 第一册3.2 函数的基本性质课文内容课件ppt: 这是一份高中数学人教A版 (2019)必修 第一册<a href="/sx/tb_c4000268_t3/?tag_id=26" target="_blank">3.2 函数的基本性质课文内容课件ppt</a>,共40页。PPT课件主要包含了自主预习·新知导学,合作探究·释疑解惑,思想方法,随堂练习,答案C等内容,欢迎下载使用。
高中数学人教A版 (2019)必修 第一册第三章 函数的概念与性质3.2 函数的基本性质教案配套课件ppt: 这是一份高中数学人教A版 (2019)必修 第一册<a href="/sx/tb_c4000268_t3/?tag_id=26" target="_blank">第三章 函数的概念与性质3.2 函数的基本性质教案配套课件ppt</a>,共41页。
高中数学人教A版 (2019)必修 第一册3.2 函数的基本性质课文内容课件ppt: 这是一份高中数学人教A版 (2019)必修 第一册3.2 函数的基本性质课文内容课件ppt,共18页。PPT课件主要包含了导入新课,精彩课堂,应用举例,课堂练习,课堂总结等内容,欢迎下载使用。














