2023年高考数学人教A版（2019）大一轮复习--2.2　基本不等式（课件）

这是一份2023年高考数学人教A版（2019）大一轮复习--2.2　基本不等式（课件），共48页。PPT课件主要包含了内容索引，强基础增分策略，增素能精准突破，知识梳理，a0b0，常用结论，答案C，答案AB，答案AD，方法总结等内容，欢迎下载使用。
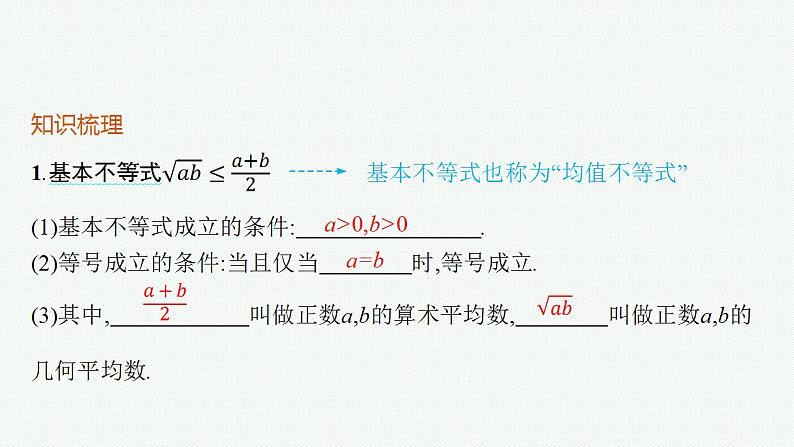
基本不等式也称为“均值不等式”
(1)基本不等式成立的条件:　　　　　　　　. (2)等号成立的条件:当且仅当　　　　时,等号成立. (3)其中,　　　　　　叫做正数a,b的算术平均数,　　　　叫做正数a,b的几何平均数. 
2.几个重要的不等式(1)a2+b2≥　　　　(a,b∈R),当且仅当a=b时,等号成立. 
3.利用基本不等式求最值已知x≥0,y≥0.(1)如果积xy等于定值P,那么当　　　　时,和x+y有最小值　　　　(简记:积定和最小). (2)如果和x+y等于定值S,那么当　　　　时,积xy有最大值　　　　(简记:和定积最大). 
微点拨利用基本不等式求最值的注意点(1)应用基本不等式求最值应满足“一正、二定、三相等”,忽略某一条件就会导致错误.(2)应用基本不等式求最值时应尽量避免多次运用基本不等式,若必须多次使用,一定要保证它们的等号成立的条件一致.
对点演练1.判断下列结论是否正确,正确的画“√”,错误的画“×”.
2.下列结论不成立的是(　　)A.若a,b∈R,则a10+b10≥2a5b5
A.5B.1C.-5D.-1
典例突破例1.(多选)(2021浙江杭州高三月考)已知正实数a,b满足a+b=1,则下列不等式成立的有(　　)
名师点析利用基本不等式判断命题真假的注意点(1)要熟记基本不等式及其各种变形的形式与成立的条件,明确其中等号成立的条件.(2)理解基本不等式的一般性,基本不等式中,a,b可以换成不同的数、式,但必须满足相应的条件,否则就会得出错误的结论.
对点训练1(多选)(2021山东青岛高三月考)下列不等式的证明过程正确的是(　　)
考向1.通过拼凑利用基本不等式求最值典例突破
答案 (1)A　(2)
对点训练2(2021广东湛江高三一模)已知a,b∈R,若a-3b=2,则2a+ 的最小值为　　　　　. 
考向2.通过常数代换利用基本不等式求最值典例突破例3.(2021山东潍坊高三期中)已知a>0,b>0,且a+2b=3ab,则ab的最小值为(　　)
方法点拨常数代换法求最值
对点训练3(2021重庆八中高三月考)若实数x,y满足x>2y>0,且xy=1,则 的最小值是　　　　　. 
考向3.通过消元利用基本不等式求最值典例突破
例4.(2021辽宁锦州高三期中)已知正实数x,y满足x-2y=1,则 +y的最小值为　　　　　. 
名师点析消元法求最值在条件最值问题中,当含有多个变量时,可以根据已知条件,用一个变量表示另一个变量,从而将欲求最值的代数式中的变量减少,只保留一个变量,然后通过拼凑,创造符合基本不等式应用的条件,求得最值.
考向4.利用基本不等式“和”“积”互化求最值典例突破
例5.(2021河北沧州高三期末)已知正数a,b满足 =3,则a+b的取值范围是　　　　　;ab的最小值为　　　　　. 
名师点析“和”“积”互化求最值的方法(1)基本不等式具有将“和式”转化为“积式”和将“积式”转化为“和式”的放缩功能,因此可以用在一些不等式的证明中,还可以用于求代数式的最值.(2)在解决条件最值时,如果条件等式中,含有两个变量的和与积的形式,可以直接利用均值不等式对两个正数的和与积进行转化,然后通过解不等式进行求解,或者通过构造一元二次方程,利用根的分布解决问题.
对点训练5(2021天津和平高三期中)若正数a,b满足2a+b+6=ab,则ab的最小值为　　　　　. 
考向5.通过多次利用基本不等式求最值典例突破例6.若a>0,b>0,则 +b的最小值为　　　　. 
易错警示多次利用基本不等式求最值的注意点(1)注意对代数式进行合理地转化,转化不当则无法连续运用基本不等式;(2)当多次连续运用基本不等式时,应确保每次使用的基本不等式中等号成立的条件是一致的,否则,相应的最值是取不到的.
对点训练6若a>b>0,则a2+ 的最小值为　　　　　. 
考向1.基本不等式与其他知识的综合典例突破
A.34B.32C.30D.28
名师点析基本不等式是求最值的一种重要方法,因此具有广泛的应用,在三角函数、数列、平面向量、立体几何等综合问题中,常常利用基本不等式求得最值.
考向2.基本不等式的实际应用典例突破
名师点析利用基本不等式解决实际问题的方法(1)理解题意,明确数量关系,引进变量,注意设变量时,一般把求最大值或最小值的量定义为函数.(2)根据题意抽象出函数解析式,利用基本不等式求函数的最值.(3)求最值时,注意在函数定义域内求解,并验证等号成立的条件.
对点训练8(2021湖南长沙高三期中)由于近年来,冬季气候干燥,冷空气频繁袭来,为提高公民的取暖水平,某社区决定建立一个取暖供热站.已知供热站每月自然消费与供热站到社区的距离成反比,每月供热费与供热站到社区的距离成正比,如果在距离社区20千米处建立供热站,这两项费用分别为5千元和8万元,那么要使这两项费用之和最小,供热站应建在离社区(　　)A.5千米处B.6千米处C.7千米处D.8千米处